一道双曲线模考题的探究
于晓强 林国红
广东省佛山市顺德区乐从中学 (528315)
1.题目再现
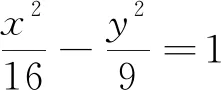
分析:本题是解析几何的一道综合问题,知识方面主要考查了双曲线的定义、焦半径、圆的方程和圆与双曲线的位置关系等知识点;思想方面考查了特殊与一般、化归与转化、函数与方程、数形结合等数学思想方法;突出考察学生对数量转化,运算能力,推理论证能力.试题条件简洁,解法多样,背景丰富,是一个值得深入探究的好题.
2.解法探究

图1
解法1:(特殊点法)如图1,令A为双曲线的右焦点,则F(-5,0),A(5,0),所以
|FM|=|NA|,
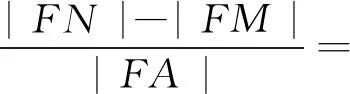
评注:解法1取了满足条件的特殊点右焦点为A,因A点在x轴上且在F的右侧一个任意的点,所以满足题意的任一A点,得到的结果都一样,同时体现了特殊代替一般的数学解题方法.
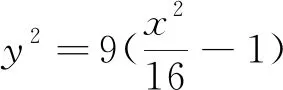

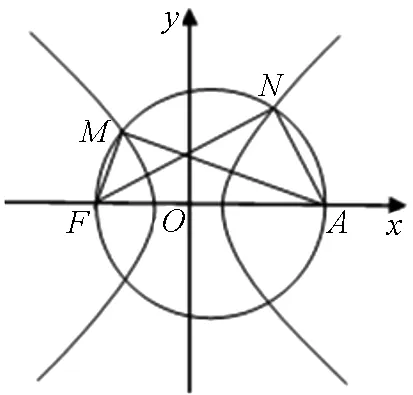
图2

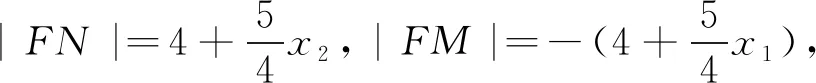
评注:两种解法实质都是交点满足的一元二次方程,利用韦达定理和双曲线的焦半径公式表示出|FM|,|FN|的长,代入所求式子中化简得到结果.不同的是交点满足的一元二次方程时解法2是把圆的方程与双曲线方程联立方程组,消去y得到关于x的一元二次方程,体现了方程组的思想;而另解中是利用直径所对圆周角为直径的性质分别得到两个交点横坐标的一元二次方程,再抽象出双曲线与圆的交点方程,体现了抽象思维的训练.

图3
解法3:(向量法)如图3,设双曲线的右焦点为F2,并设|FM|=m,|FN|=n,|FA|=t,由题意可得
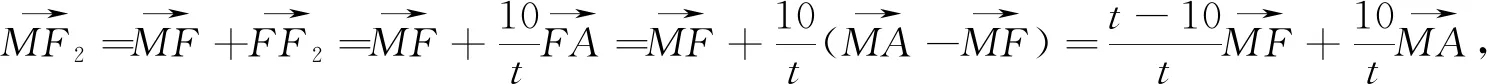

评注:向量作为工具,应用比较广泛,特别是在解析几何中.本题是线段长度的计算可以转化为向量大小的求解,利用双曲线的定义构建出焦点三角形,用向量的线性运算找到等量关系,抓住几何特征,将等量关系平方化简得到向量大小的等量关系,化简整理出所求式子的结果.
解法4:(余弦定理)如图3,设双曲线的右焦点为F2,并设|FM|=m,|FN|=n,|FA|=t,由题意可得:
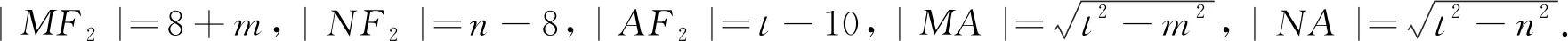
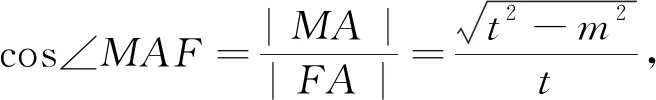
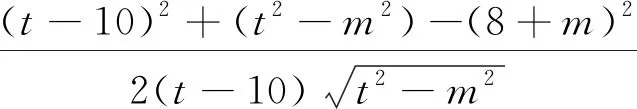
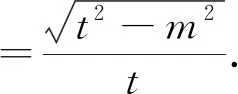
同理可得t[(t-10)2+(t2-n2)-(n-8)2]=2(t-10)(t2-n2)②.

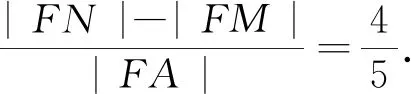
评注:这种解法的基本思路是有关线段长度的计算,可以先把线段长度设出来,抓住焦半径的应用,然后利用双曲线的定义构建出焦点三角形,并表示出三角形的各边,选择一些等量角度,应用余弦定理建立所求线段长度的等量关系,化简得到所求结果的值.
3.结论推广


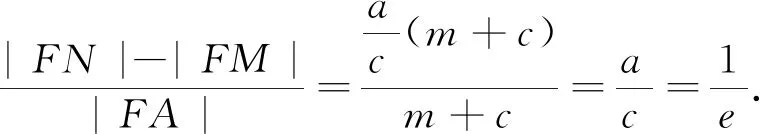
4.类比性质
我们知道,双曲线,抛物线与椭圆都是圆锥曲线,很多时侯三者之间有可类比的性质,这体现了圆锥曲线性质的内在统一的和谐美.那么椭圆与抛物线是不是也有类似于结论1的性质呢?经探究,得到如下结论:

图4
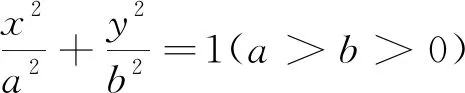

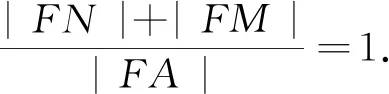
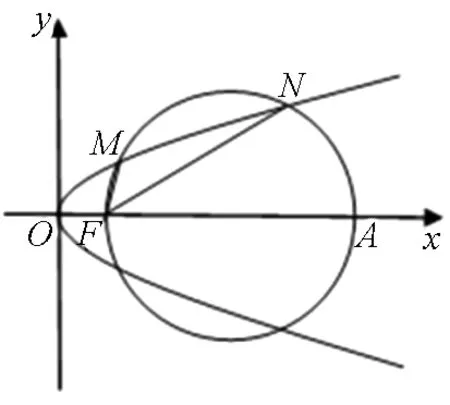
图5
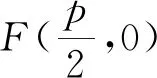
5.结语
对题目的拓展、引申、变式探究是一名数学教师必备的专业素养,平时要重视对典型问题进行深入研究,探研规律,并适当拓展,充分挖掘题目的育人价值.高中数学新课程理念之一是倡导积极主动、勇于探索的学习方式.在教学中,要引导学生不要只满足于问题的解决,而是要通过变式、类比进行研究,寻求问题的增长点,从而达到做一题会一类,甚至会一片的目的;让学生体验数学的发现和创造历程,引导他们勇于发现问题、提出问题、解决问题,让学生在解题思路上产生质的变化,使思维得到发展,进而全面提高学生的综合能力,提升学生的数学核心素养.

