Reliability estimation of rotary lip seal in aircraft utility system based on time-varying dependence degradation model and its experimental validation

Cho ZHANG, Rentong CHEN, Gunghn BAI, Shoping WANG,Milet M. TOMOVIC

a School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China

b Research Institute of Frontier Science, Beihang University, Beijing 100083, China

c College of Intelligent Science and Technology, National University of Defense Technology, Changsha 410073, China

d Engineering Technology Department, Old Dominion University, Norfolk, VA 23529, USA

KEYWORDS Bayesian approach;Dependence analysis;Reliability estimation;Rotary lip seal;Time-varying copula function

Abstract With several attractive properties, rotary lip seals are widely used in aircraft utility system,and their reliability estimation has drawn more and more attention.This work proposes a reliability estimation approach based on time-varying dependence analysis. The dependence between the two performance indicators of rotary lip seals,namely leakage rate and friction torque,is modeled by time-varying copula function with polynomial to denote the time-varying parameters, and an efficient copula selection approach is utilized to select the optimal copula function. Parameter estimation is carried out based on a Bayesian method and the reliability during the whole lifetime is calculated based on a Monte Carlo method.Degradation test for rotary lip seal is conducted and the proposed model is validated by test data. The optimal copula function and optimal order of polynomial are determined based on test data.Results show that this model is effective in estimating the reliability of rotary lip seals and can achieve a better goodness of fit.

1. Introduction

Rotary lip seals are widely used in fuel pumps and various other types of mechanical components in aircraft utility system due to its attractive properties,namely high thermal resistance,low cost, good sealing performance, and high oil resistance.1,2Failure of rotary lip seals may result in fuel leak or other types of error and malfunction in aircraft utility system, and thus lead to numerous economic loss or even catastrophic consequences. Therefore, it is important to accurately predict the reliability of rotary lip seals during operation to ensure flight safety.

For mechanical components which have very long lifetime,there is usually lack of failure data. For this reason, degradation testing (DT) and accelerated degradation testing (ADT)have been widely conducted to evaluate the reliability of such highly reliable mechanical components.3Morrell et al.used the compression set properties and oxygen uptake as performance indicators and studied the accelerated degradation of nitrile rubber O-rings during an accelerated degradation testing.4Zhang et al. used Gamma process to describe the degradation for products with monotonic degradation process in ADT and proposed a reliability demonstration method.5De Carlo et al.applied ADT on a new mechanical subassembly of a washing machine and identified the most appropriate degradation parameter.6For rotary lip seals, several parameters including leakage rate, friction torque, stress of the lip, etc., could be used as performance indicators in the degradation testing or accelerated degradation testing of them. In these performance indicators which could reflect the functioning and degradation of rotary lip seals, leakage rate and friction torque could be collected online, and are preferred in many applications.

Usually for many mechanical components,different performance indicators may be statistically dependent because of commonly shared factors including environmental or operational stress, material properties or wear history.7For rotary lip seals, as will be described in the next section, leakage rate and friction torque are both affected by wear and aging, and it is necessary to assume that the two performance indicators are dependent. Thus, a joint bivariate probabilistic model is needed to describe the dependence between leakage rate and friction torque. Traditional joint bivariate distribution could be used to describe the dependence between two marginal distributions. However, a traditional joint bivariate distribution often assumes that the marginal distributions are from identical distribution families. In addition, only linear dependence could be modeled. Such assumptions are usually very restrictive and cannot be easily met in practical applications.

Copulas allow us to model the marginal behavior and dependence structure separately, which offers more flexibility in describing the dependence between marginal distributions.8,9For this reason, they have been widely utilized to describe the dependence in many fields, including financial markets,10,11wind energy,12,13and reliability analysis or lifetime evaluation of mechanical components.14,15Copulas have also been used in the dependence analysis of different performance indicators of mechanical components. Chen et al. used copula function to characterize the failure dependence between subsystems of mechanical systems and proposed the reliability improvement method according to relative failure rate.16Zhang et al.proposed a multi-dimensional copula construction method and used it in the lifetime estimation in accelerated life testing.17In these studies,the copula function,which was used for capturing the dependence, was assumed to be known in advance. However, in many applications, the marginal distributions might not lead to one specific type of copula to relate them.Therefore,methods which can select appropriate copula should be considered.Pan et al.used copula to characterize the dependence between different degradation paths of products and selected the best copula by calculating Akaike information criterion (AIC).18Wang et al. built a Bayesian reliability evaluation model for ADT and determined the optimal prior distribution by analyzing the accuracy of the estimated parameter values.19

However, all these studies utilized copulas with constant parameters.For rotary lip seals,as will be described in the next section, the dependence between leakage rate and friction torque could be time-varying. Time-varying copulas have been applied in financial analysis.20There are two approaches to describe the time variation of the dependence between the two marginal distributions. The first approach is to use different forms of copula at different periods,21and the other is to let the form of copula remain fixed and the parameters in the copula change with time.22The first approach assumes that the dependence structure changes with time,and this might be appropriate when the common factor behind the dependent variables is different from time to time. The second approach assumes that the common factor behind the dependent variables remains the same, but the impact of the factor on the dependent variables changes with time. For rotary lip seals,the common factors which affect the two performance indicators, i.e., leakage rate and friction torque are wear and aging,and this does not change for the whole lifetime. However, the effect of the two failure modes on the two performance indicators would vary with the wear rate and chemical reaction rate which inevitably change with time. For this reason, in this work we choose the second approach to describe the timevarying dependence between the two performance indicators.

Several types of time-varying copulas have been utilized in financial and economic analysis based on the second approach.23It was also shown in Refs. 24,25 that these timevarying copulas could achieve lower AIC or BIC, higher loglikelihood or better precision. However, as pointed in Ref.20, these reported time-varying copulas have been proposed specifically for financial or economic purposes where there are often lots of fluctuations, and they might not be appropriate for modeling dependent degradation processes of mechanical system which are relatively smooth. Pan et al. studied the lifetime estimation of nitrile butadiene rubber O-rings under storage conditions using time-varying copula.26Two performance characters, namely, compression set and compressive stress relaxation were considered, and a bivariate timevarying copula model was used to capture the statistical dependence between the two performance characteristics. A copula selection approach was proposed to determine the timevarying copula function. It is shown that the reported approach in Ref.26 is an efficient method and can achieve better goodness of fit comparing with previously reported timevarying copulas.

However, there are several limitations in Ref. 26. Firstly,the method used for developing marginal degradation model in Ref. 26 is not general and systematic for other mechanical components or systems. For instance, the normal distribution and Weibull distribution were selected as the marginal distribution of the two performance indicators respectively in Ref.26, based on engineering experience. These two distributions may not be appropriate for performance indicators of other mechanical systems, such as leakage rate and friction torque of rotary lip seals. Further distribution selection procedure based on statistical tests are needed if no engineering experience is available. In addition, it is assumed that the shape parameters of the normal and Weibull distributions were invariant at different stresses in Ref. 26. However, the shape parameter of the normal distribution can vary with stress.Thus, further statistical tests, such as Hartley’s test and Bartlett’s test are needed. If they fail the corresponding tests, the models as well as the statistical inference will be much more complicated when both shape parameter and scale parameter are functions of stress and time.Thus,a more general and systematic method is needed to develop the marginal degradation model for the performance indicators.

Secondly, the autoregressive-moving-average (ARMA)process is used in Ref.26 as evolution equation for the parameters of time-varying copula.Although the ARMA process has been used to model the time-varying parameter of the copula function in financial analysis and reliability analysis, there is no validation of their appropriateness to model the timevarying parameter of the copula function used for estimating the lifetime of mechanical components or system. Virtually,there are usually lots of fluctuations in the data of financial or economic analysis, in which ARMA may be appropriate.But the degradation path of rotary lip seal is relatively smooth,the dependence of the marginal distributions at these two situations could be different from those in financial or economic analysis. Thus, a more appropriate evolution equation is needed for the parameters of time-varying copula used in mechanical system.

Based on the above discussion, an improved time-varying dependence degradation model is developed and applied to reliability estimation of rotary lip seal.Firstly,the degradation process of each performance indicator is regarded as a stochastic process with different parameters.Wiener process is utilized to develop the marginal degradation model of leakage rate and friction torque of rotary lip seals. Secondly, because the timevarying dependence between leakage rate and friction torque is relatively smooth and might include several inflection points in its lifetime, a polynomial function is used as evolution equation for the parameters of time-varying copula. Deviance Information Criterion (DIC) is adopted as criteria to find the optimal order for the polynomial for statistical inference of the parameters of time-varying copula. Thirdly, a two-stage Bayesian approach is utilized to estimate the parameters of marginal degradation model and bivariate copula model successively. After the parameters are estimated, the reliability analysis of rotary lip seal based on a Monte-Carlo method is carried out.

The rest of the paper is organized as follows. In Section 2,the structure and fault mechanism of rotary lip seal is briefly introduced, and the degradation model for rotary lip seal based on time-varying copula is built. In Section 3, the twostage Bayesian approach is introduced.In Section 4,the degradation test for rotary lip seal with sample number eight is conducted, and estimation of parameters regarding the degradation process and the dependence between different performance indicators are carried out. After the optimal copula function and optimal order for the polynomial is determined,the reliability of rotary lip seal based on time-varying dependence degradation model is calculated and analyzed. The conclusions are in Section 5.

2. Degradation model development of rotary lip seal based on time-varying copula

2.1. Structure and fault mechanism of rotary lip seal

The schematic of a rotary lip seal is shown in Fig. 1.It can be seen that a rotary lip seal is composed of a steel frame,an elastomeric ring and a garter spring.A preload to the shaft is usually produced by the steel frame and the elastomeric ring. A garter spring which can provide additional force is also commonly used.

When a well-designed rotary lip seal is operating, a micron scale film of fluid will be generated in the lip-shaft interface in the sealing zone.A pumping action from the air side to the liquid side of the seal will be simultaneously generated by the combined action of lip surface asperities, shear deformation and the contact characteristics of the lip-shaft interface.27This pumping action will help to reduce or prevent leakage of the seal and the reverse pumping rate is one of the most important performance characteristics of rotary lip seal. If the reverse pumping rate is not big enough, leakage might occur.

For rotary lip seals,leakage rate and friction torque are two important performance indicators.28When a rotary lip seal is in operation, material of the lip will gradually lose because of wear, and this will induce change of the lip surface micro topography. The pumping action of the lip seal will thus be affected by the change of micro topography and this will lead to the change of pumping rate and the leakage. Additionally,the wear extent of rotary lip seal is also correlated with the friction torque.29,30

As rubber is usually used as the material for the elastomeric ring of rotary lip seal,aging is also one of the important failure modes of rotary lip seal.31Aging affects the tensile strength,elongation and hardness of rotary lip seal, and has significant effects on the pumping action and friction torque during the operation of lip seal.32When temperature increases, the compression set of rotary lip seal will increase dramatically, and the stress-strain ratio and friction torque will also increase.31The pumping rate,which is one of the most important performance characteristics of rotary lip seal,will gradually decrease when temperature increases.31The dependence between these performance indicators could also change when temperature changes during the operation of rotary lip seal.

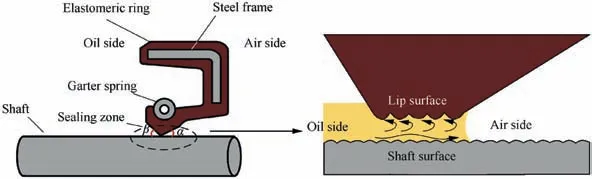
Fig. 1 Schematic of a rotary lip seal and reverse pumping affect.

It can be seen from above analysis that both leakage rate and friction torque are affected by wear and aging, and it is reasonable to assume that they are dependent. In addition,as wear rate and aging rate of rotary lip seal vary with time during the operation, the dependence between leakage rate and friction torque could also be time-varying.The simulation and experimental results of Guo et al.showed that the friction torque of rotary lip seal firstly increases,then slowly decreases during operation. On the other hand, during operation the pumping rate keeps decreasing, but the decrease rate firstly keeps big, then turns smaller.31,33These results also indicate that the dependence between the two performance indicators of rotary lip seal could be time-varying.In addition,the degradation path for friction torque is not monotonic.In the following subsection, assuming that each performance indicator follows Wiener process, which can be used to describe nonmonotonic degradation process, the degradation model of rotary lip seal based on time-varying dependence analysis is built.

2.2. One-dimensional degradation model based on Wiener process

where Tihas an inverse Gaussian distribution, and diis the failure threshold of the ith performance indicator. The cumulative distribution function can be given by

2.3.Degradation model for rotary lip seal based on time-varying copula and log-likelihood function derivation

The parameters in Eq. (7) can be divided into two groups.The first group includes those regarding Wiener process and we use α to denote them,i.e.α=(μ1，σ1，q1;μ2，σ2，q2).The second group includes those regarding the copula function and is denoted by θ.

Note that in Eq.(7),θ is constant,i.e.the strength of dependence remains constant in the whole degradation process.However, as mentioned in the last subsection, dependence of the two degradation indicators,i.e.friction torque and leakage rate,is time-varying in the whole degradation process.To capture the time-variance of the dependence of the two degradation indicators, we assume θ to be a function of time t.

Here polynomial is used to denote θ(t).As life for rotary lip seal is usually long,polynomial with higher order might better describe the dependence of the two performance indicators during the whole degradation process. However, if the order of polynomial is too high, overfitting might occur. Therefore,the optimal order of θ(t) needs to be determined. Constant function, i.e. time-invariant function is also considered and is used as comparison.

Results based on ARMA method adopted in Ref.26are also obtained and are used as comparison. ARMA describes a stationary stochastic process in terms of two parts, i.e., the auto regression (AR) model and the moving average (MA)model. The AR model describes the relationship between historical values and current values,and the MA model describes the error accumulation of AR model. Expression of ARMA method can be given by

2.4. Copula selection and reliability analysis

An appropriate copula function needs to be selected in order to model the dependence between the two performance indicators.However,if we use polynomial with the order of three as evolution equation, the number of parameters to be estimated is three for copulas with one parameter.For copulas with two constant parameters,this number would be six. In this case, it would be impractical to use the traditional maximum likelihood estimation method to find a suitable time-varying copula.

For each type of copula,there are two aspects to be considered, i.e., the dependence structure and the degree of dependence. The dependence structure is determined by the functional form and the degree of dependence can be obtained by the parameters. For rotary lip seal, it can be assumed that the dependence structure between the two performance indicators remain constant during the whole degradation process.For this reason, we adopt the following approach to find the optimal time-varying copula.

Firstly,find an optimal copula with constant parameters.In this step, we find an optimal copula with constant parameters to model the dependence between the two performance indicators of rotary lip seal. A two-stage Bayesian method, which will be introduced in detail in the next section, is used to estimate the parameters.

Secondly, incorporate time-varying parameters into the selected copula.In this step,after finding the copula with constant parameters which achieves the lowest DIC, the timevarying parameters are incorporated into the selected copula.We also use the two-stage Bayesian method to estimate the values of the time-varying parameters.

After the parameters are estimated based on the degradation model, the reliability function corresponding to each performance indicator can be obtained.Based on the time-varying copula function, the reliability for rotary lip seal during the whole lifetime can be calculated. In this work, a Monte Carlo based method is used to calculated the reliability for rotary lip seal during the whole lifetime. In this method, if either of the two performance indicators exceeds the corresponding threshold, the rotary lip seal is assumed to be in failure state. The steps of this method are as follows.35

(1) Calculate a number of maximum values at time t of the two performance indicators based on the degradation model and Monte Carlo method. Here we use H to denote the number of maximum values.The set of these maximum values can be denoted as[(x11，max(t)，x12，max(t))，...，(xH1，max(t)，xH2，max(t))].

(2) Count the number of values of which both performance indicators are less than their thresholds,i.e.,the number of × marks which fall into the rectangular in Fig. 2.Here the number of values of which both performance indicators are less than their thresholds is denoted by h.

(3) Then the reliability at time t can be expressed by R(t)=h/H.

3. Parameter estimation with a two-stage Bayesian approach

In the proposed degradation model, the parameters which need to be estimated can be divided into two groups. The first group includes those regarding the Wiener degradation process,and the second group includes those regarding the copula function.Correspondingly,we divide the parameter estimation process into two stages. In the first stage, the parameters regarding the Wiener degradation process are estimated based on Bayesian method. In the second stage, the parameters regarding the copula function are also estimated based on Bayesian method. Cumulative distributions in the first stage are calculated and used as the input in the second stage. Procedure of the two-stage Bayesian method can be seen in Fig.3.

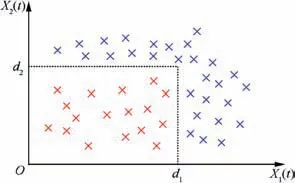
Fig. 2 Reliability calculation based on Monte Carlo method.

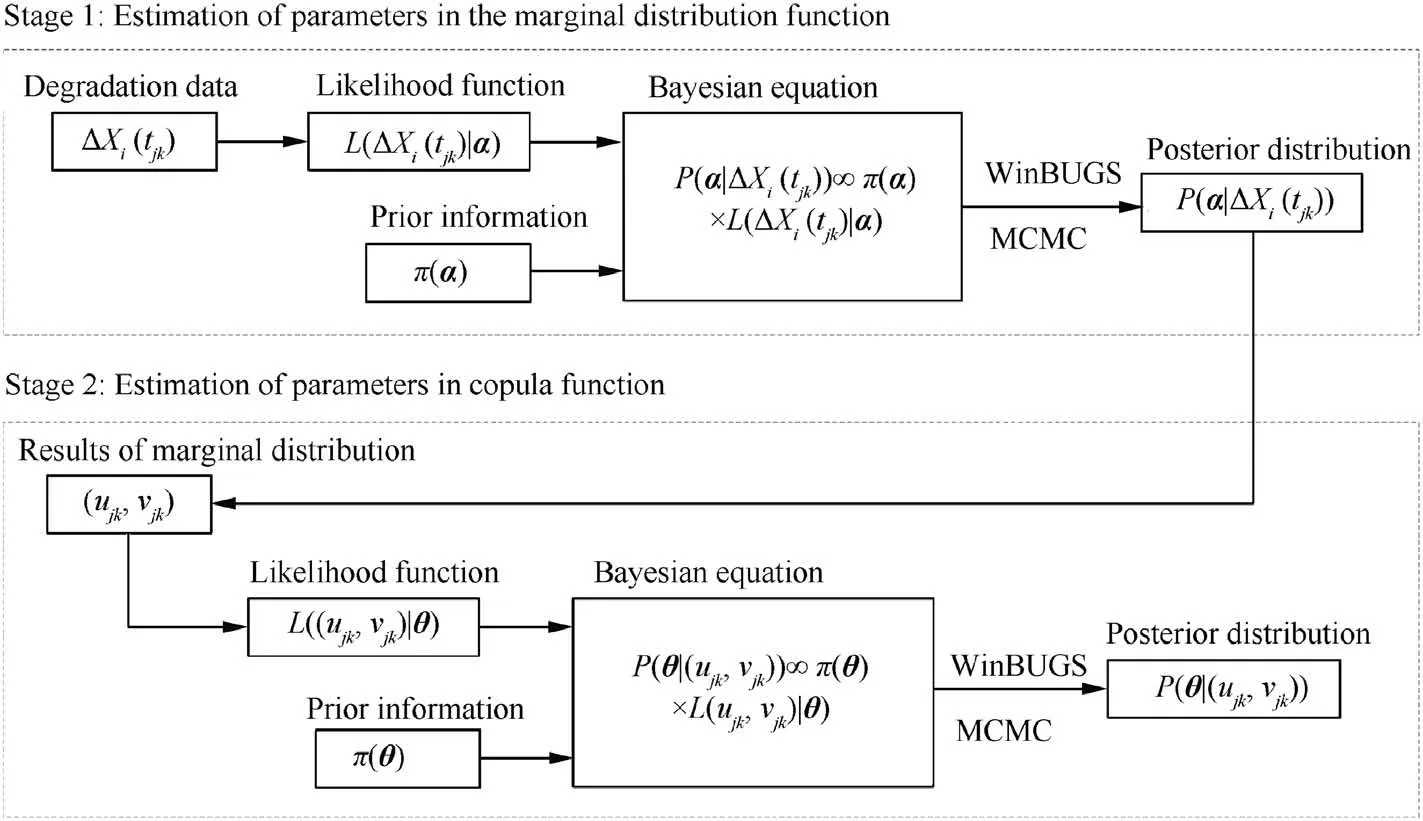
Fig. 3 Procedure of the two-stage Bayesian method.

Both Akaike’s Information Criterion (AIC) and Bayesian Information Criterion(BIC)are frequently used when comparing Bayesian models. However, the comparison based on the two methods will become difficult when the Bayesian model is complex.36DIC was proposed by Spiegelhalter et al. and uses the Bayesian model’s deviance and effective number of parameters to evaluate the model.37DIC is intended as a generalization of AIC. Model with the minimum DIC assumes that the model will make the optimal short-term predictions,and this is in the same spirit as AIC. BIC was developed by Gideon E. Schwarz and it is partly based on the likelihood function. DIC differs from BIC in both form and aims.37The Bayesian deviance of a Bayesian model is denoted as D(θ), and can be expressed by

It has been found by Celeux et al. that the Bayesian model with the lowest DIC can be regarded as the optimal model.38For complicated Bayesian models, comparison based on AIC and BIC will become difficult and in this case, comparison based on DIC could be more effective.38In this work, we use the DIC to find the best copula candidate and optimal polynomial order.

Based on the two-stage Bayesian method, in the following section, parameters regarding the degradation process are firstly estimated, then parameters regarding the dependence between the two performance indicators are estimated and different copula functions are compared. The flowchart for parameter estimation and validation is shown in Fig. 4.

4. Experimental validation

4.1. Introduction to the experiment

The accelerated degradation testing of rotary lip seal was carried out. One set of the testing equipment is shown in Fig. 5,and there were two sets of them.Fig.5(a)shows the entire testing equipment, and Fig. 5(b) shows the test module, i.e., the area marked by a red circle in Fig.5(a).In Fig.5(b),the sealed cavity is in the center of the manifold,and the seal under test is installed at the bottom of the sealed cavity. The shaft was driven by a brushless DC motor which can reach a maximum rotation speed of 6000 rpm.

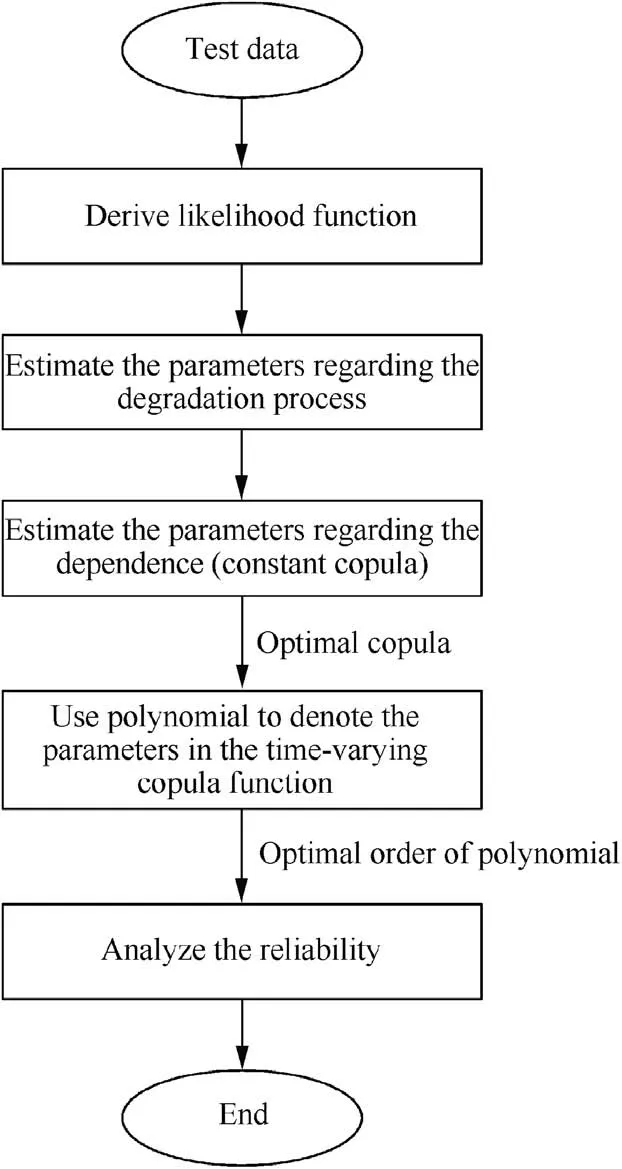
Fig. 4 Flowchart for parameter estimation and validation.

Fig. 5 One set of testing equipment of rotary lip seal.

Profile of the test module is shown in Fig. 6. The shaft is connected to a brushless DC motor by a coupling with a friction torque sensor integrated inside.As working media for this type of rotary lip seal is jet fuel,there is an external fuel power source to provide pressurized fuel into the sealed cavity in the test module. The shaft is made of polymethyl methacrylate,which is a type of transparent material. There was a micro camera to monitor the micro topography of the contact area of the lip seal through the transparent shaft, as shown in Fig. 6. A micro temperature sensor is utilized to monitor the temperature of the lip.

Working pressure for the tested rotary lip seal was 0.04 MPa. Other parameters of the tested rotary lip seal are shown in Table 1.

Schematic of the test rig is shown in Fig.7.Friction torque,temperature of the lip and leakage were measured. The signal was conditioned by a signal conditioning module and collected by data collection system.An NI PXI was used for data collection and processing. Data collection software was programmed by National Instruments LabVIEW®. Data collection was performed every four hours automatically.For friction torque signal, each time of collection lasted for 10 seconds and the sample rate was 100 Hz. Temperature of the lip and leakage rate were measured at the middle of each time of collection. Failure of every rotary lip seal under test was judged by the temperature of the lip, friction torque and leakage manually. Information collected by the micro camera was also sent to the test operators, and was referred to when performing the failure diagnosis of the seals under test. Each time a rotary lip seal failed, it was dismounted and a new one was installed, then the test of the newly installed rotary lip seal started.

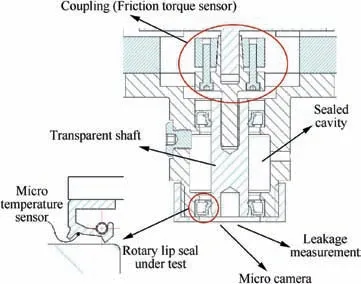
Fig. 6 Profile of the test module.

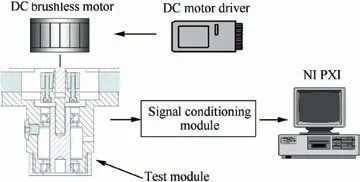
Fig. 7 Schematic of test rig.

From the user’s manual,typical rotation speed for this type of rotary lip seal is 2500 r/min, and typical operation temperature is 25°C. Maximum rotation speed and temperature under which this type of rotary lip seal does not change failure mechanism are 9554 r/min and 200°C, respectively. There were eight tested rotary lip seals and they were classified into two groups. The number of samples in each group was four.Stress level for each group of tested rotary lip seals is shown in Table 2. The first group worked under typical operation condition, and stress level of the second group was a little higher than that of typical operation condition. Stress level of the second group is still much lower than the maximum rotation speed and temperature, i.e., 9554 r/min and 200°C.Therefore, failure mode of samples in the second group will be the same as that in the first group.

4.2.Estimation of parameters regarding the degradation process(The first stage of the two-stage Bayesian approach)

For both constant and time-varying copula function, parameters regarding the degradation process are firstly estimated by the two-stage Bayesian approach.The programs were coded in WinBUGS and were implemented on a desktop computer with Intel Core i7-7700 CPU and 16 GB of RAM. Prior distributions of all six parameters in α are set as non-informative priordistribution. The number of iterations is set as 100,000. After the MCMC simulation starts, the Gelman-Rubin ratio of the parameters are firstly monitored to determine whether the distribution has converged, as shown in Fig. 8. It can be seen from Fig. 8 that distribution of all parameters quickly converges after 5000 iterations. A total of 90,000 iterations, i.e.,from 10,001 to 100,000, are chosen as samples and are used to compute the mean value of each parameter.The calculation of this step takes 62 s.

Table 2 Applied stresses for the two groups of tested rotary lip seals.

4.3.Estimation of parameters regarding the dependence between different performance indicators and copula function selection(The second stage of the two-stage Bayesian approach)

Firstly,we select the most suitable fitting copula function with constant parameters. We adopted the following copula candi-dates, Clayton, Frank, Gumbel, Plackett, AMH, and symmetrized Joe-Clayton (SJC) copulas. Another type of copula which belongs to Archimedean copula family was also adopted, which is denoted as Type-I copula in this work.Expression and density function of this type of copula can be found in the Appendix. The number of parameters is two for the SJC copula and one for the other copula candidates.The estimation results when parameters are constant are shown in Table 4.It can be seen from Table 4 that the Plackett copula yields the lowest DIC, with an estimated parameter equal to 30.74.

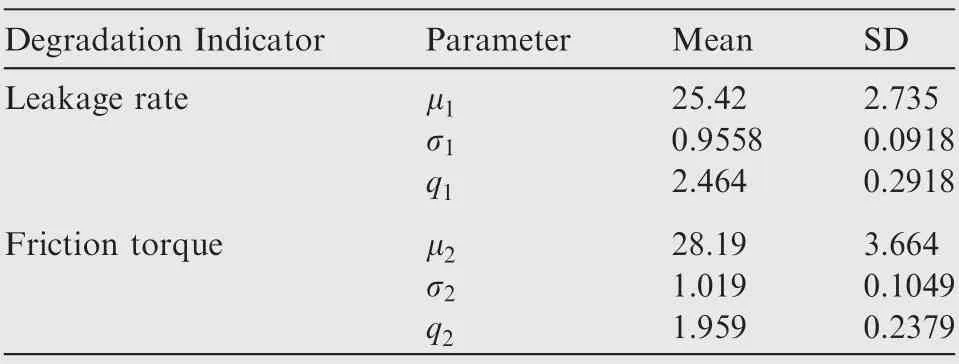
Table 3 Mean and SD of the parameters regarding the degradation process.

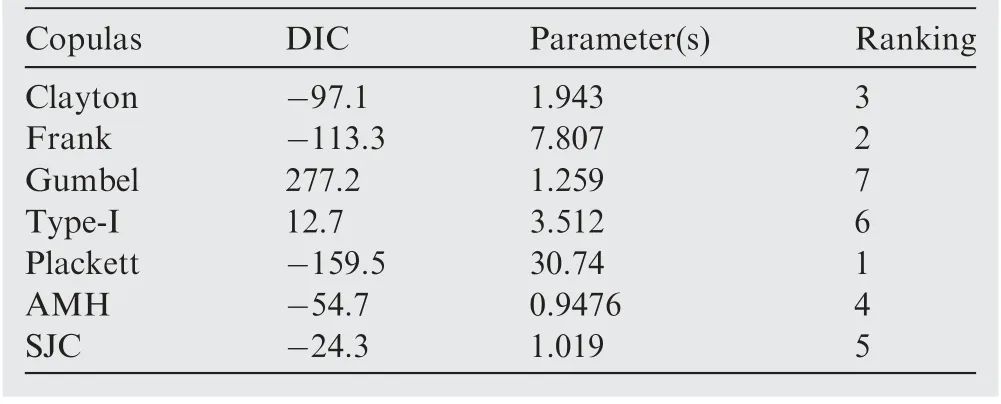
Table 4 Results of copula fitting (Constant).

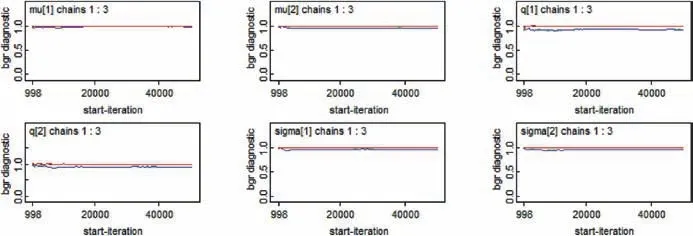
Fig. 8 Gelman-Rubin ratio of the parameters regarding the degradation process.

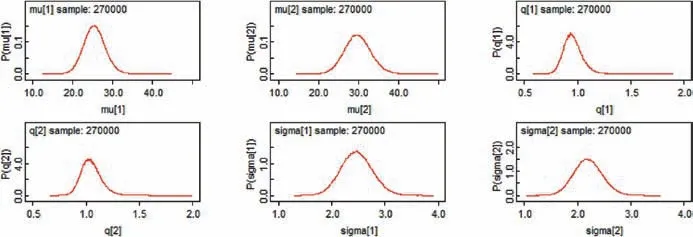
Fig. 9 Posterior distribution of the parameters regarding the degradation process.

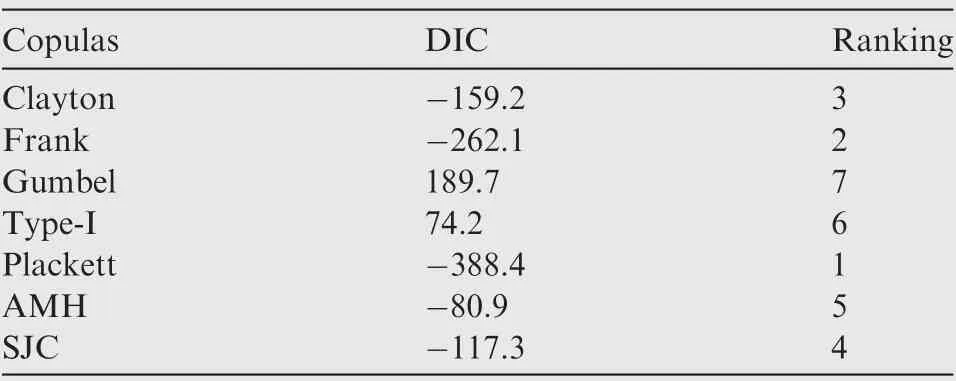
Table 5 Results of copula fitting (Linear function).

Table 6 Results of copula fitting (quadratic function).

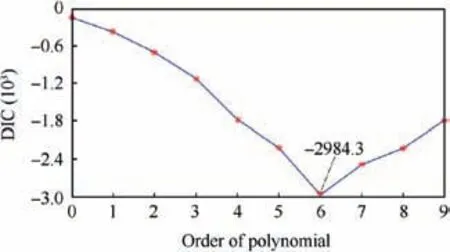
Fig. 10 DIC results for different orders of polynomial in Plackett copula.

Then Plackett copula is used for developing the timevarying copula in the second stage. Linear function, i.e.,θ1(t)=a1t+b1is firstly used to denote the parameters in the time-varying copula function, and the estimation results can be calculated. Results for the other six types of copulas with linear function to denote θ(t) are also calculated and are used as comparison. The estimation results are shown in Table 5.

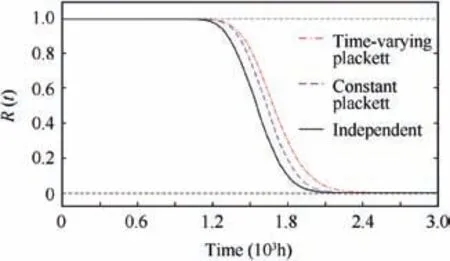
Fig. 11 Reliability analysis of tested rotary lip seal.

Quadratic function, i.e., θ2(t)=a2t2+b2t+c2is then used to denote the parameters in the time-varying copula function.Results for Plackett copula and the other six types of copulas in this case are shown in Table 6. It can be seen from Table 5 and Table 6 that for linear function and quadratic function,the ranking based on DIC for the seven copulas is not exactly the same. However, at both cases, Plackett copula still yields the lowest DIC value.

Next, we continue to find the optimal order of polynomial which denotes the parameters in the time-varying copula function. As mentioned above, polynomials with higher order might better describe the change of dependence over time because they have more parameters. However, too many parameters might cause overfitting, which makes the model unable to fit additional data or predict future observations reliably. Here we use DIC to find the optimal order for the polynomial which is used to denote θ(t) in the Plackett copula function. The DICs when the order of polynomial goes from 0 to 9 are shown in Fig. 10. It can be seen from Fig. 10 that as the order of polynomial increases,the DIC of copula fitting firstly keeps decreasing, and reaches the minimum when the order of polynomial is six. Then the DIC of copula fitting starts increasing, which indicates that overfitting occurs indeed.

Parameter estimation of all time-varying copula takes a lot of time, as shown in Table 7. For example, for SJC copula which has two parameters, when the order of polynomial is six, the number of parameters to be estimated would be 14,and the parameter estimation takes 986 seconds. The calculation time for all the estimation in Table 7 is about 4 h. By the proposed approach,i.e.,finding the best fit constant copula and then using polynomial to denote time-varying parameters,the calculation would be about 35 min. In addition, this work only considers seven copula candidates. For not missing any opportunity of obtaining better copula functions, there are up to hundreds of candidates which might be taken into consideration.Therefore, the proposed approach has a significant advantage in terms of efficiency.

Table 7 Calculation time of copula fitting for different orders of polynomial (unit: s).

Table 8 Comparison of MTTF when the two performance indicators are at different dependent situations.

4.4. Reliability analysis of rotary lip seal based on time-varying dependence degradation model

Based on the method introduced in Section 3,the reliability of tested rotary lip seal was calculated, as shown in Fig. 11. In Fig. 11, ‘Time-varying Plackett’ means that the increments of the two performance indicators are described by Plackett copula with six-order polynomial to denote time-varying dependent parameter, and ‘Constant Plackett’ means that the increments of the two performance indicators are described by Plackett copula with constant dependent parameter. With the reliability results, the MTTF under each situation can be calculated, as shown in Table 8. The MTTF based on the ARMA approach in Ref. 26 is also calculated and used as comparison.

Fig. 11 shows that the reliability of tested rotary lip seal when the two performance indicators are dependent is higher than that when they are independent, indicating a positive dependence between leakage rate and friction torque. From Table 8, it can be further concluded that the MTTF when the dependence of the two performance indicators is described by time-varying Plackett copula is closer to the MTTF from manufacturer than the MTTFs for the other three situations.

5. Conclusions

This work proposes a reliability estimation model for rotary lip seals based on time-varying dependence analysis. With time-varying copula function to describe the dependence between the two performance indicators of rotary lip seals, a copula selection approach is proposed to find the optimal copula efficiently and build the degradation model.Parameter estimation is conducted based on a Bayesian method and the reliability during the whole lifetime is calculated based on a Monte Carlo method. Degradation test for rotary lip seal is carried out and validation based on test data is conducted.With polynomials as time-varying parameters in the copula function, the optimal order is also determined. Validation results show that this model is effective in estimating the reliability of rotary lip seals and can achieve a better goodness of fit.

In this work, polynomials are used to denote evolution parameters in the copula function and ARMA method is used as comparison. As there are various types of functions which can be used to denote time-varying parameters, future work should focus on finding other types of functions as evolution parameters in the copula function and assess the accuracy.Ideas derived from this work can also be extended to other types of mechanical components which have dependent performance indicators.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China(51875015,51620105010,51675019),and Natural Science Foundation of Beijing Municipality(L171003).

Appendix A. We list the functional forms of all copulas and their density function used in this paper as follows.