Loopy belief propagation based data association for extended target tracking

Zhenzhen SU, Hongbing JI, Yongquan ZHANG

School of Electronic Engineering, Xidian University, Xi’an 710071, China

KEYWORDS Belief propagation;Data association;Extended target;Graphical model;Simplified measurement set;Target tracking

Abstract The data association problem of multiple extended target tracking is very challenging because each target may generate multiple measurements. Recently, the belief propagation based multiple target tracking algorithms with high efficiency have been a research focus. Different from the belief propagation based Extended Target tracking based on Belief Propagation (ET-BP) algorithm proposed in our previous work, a new graphical model formulation of data association for multiple extended target tracking is proposed in this paper.The proposed formulation can be solved by the Loopy Belief Propagation(LBP)algorithm.Furthermore,the simplified measurement set in the ET-BP algorithm is modified to improve tracking accuracy. Finally, experiment results show that the proposed algorithm has better performance than the ET-BP and joint probabilistic data association based on the simplified measurement set algorithms in terms of accuracy and efficiency.Additionally, the convergence of the proposed algorithm is verified in the simulations.

1. Introduction

Multiple Target Tracking (MTT) is aimed at estimating the number and states of multiple targets based on the measurements of sensors.MTT problems can be divided into two main categories: Multiple Point Target Tracking (MPTT)1,2and Multiple Extended Target Tracking (METT).3-6In MPTT,each point target generates at most one measurement per time step. Different from MPTT, METT deals with extended targets whose echo occupies one or more than one resolution cell and generates one or more than one measurement per time step. Recently, due to the significant improvement in sensors resolution,METT is brought to the forefront and widely used in many applications such as autonomous driving, surveillance, sensor networks, mobile robotics, and so on. Besides,the measurement-to-track association problem is a crucial issue in MTT applications.

The existing MTT algorithms include vector model based algorithms7and set model based algorithms,8in which the multiple target states and measurements are modeled as random vectors and Random Finite Sets (RFSs), respectively.These algorithms generally have high complexity and cannot scale well with system parameters.Because of such drawbacks,they are not suitable for the applications with a large number of measurements and targets.However,it is worth noting that the graphical model9-11is an essential tool for inference and learning because the Belief Propagation (BP) algorithm can provide a principled approximation of the optimum Bayesian inference.12The BP algorithm has been successfully applied to many fields,such as sensor networks,13cooperative localization,14communication receivers,15and channel codes.16At the same time, BP based MTT algorithms have gradually become a research focus.

The RFS based algorithms generally calculate the approximation of the joint posterior Probability Density Function(PDF). Different from these algorithms, the BP algorithm can approximate the marginal posterior PDFs for each target.Recently, the BP algorithm is particularly attractive for MTT,2,12,17-21because it enables an efficient calculation of the marginal posterior PDFs for the data association problem.Some MPTT algorithms based on graphical models have been proposed. The Loopy BP (LBP) algorithm was used to solve the data association problem in situations where each sensor has a narrow field of view.17It was also used to solve the data association problem in situations where there are a fixed number of targets observed by a single sensor.18Furthermore, the algorithm was extended to solve the multisensor-multitarget detection-estimation problem,19which allows for an unknown and time-varying number of targets.The BP based algorithms above are vector modeled, where the joint posterior PDF is expressed in random vectors. The LBP algorithm was used to approximate the posterior PDF expressed by RFSs,2resulting in the Track-Oriented Marginal MeMBer/Poisson(TOMB/P) filter and the Measurement-Oriented Marginal MeMBer/Poisson (MOMB/P) filter. The approximation by the LBP algorithm dramatically improves the efficiency of the Poisson Multi-Bernoulli Mixture (PMBM) filter and promotes its application.

Although graphical models perform well in MPTT,they do not perform so well in METT due to some challenges.Because an extended target can generate one or multiple measurements per time step,the BP based algorithms in MPTT are no longer applicable in METT, and the data association problem in METT is more complicated than that in MPTT. Thus, it is important to solve the data association problem efficiently in METT. The BP based METT (ET-BP) algorithm has been proposed in our previous work,20in which the BP algorithm is applied to METT based on a Simplified Measurement Set(SMS). However, the extension state estimation has a significant deviation.In this paper,the LBP based METT algorithm is proposed, named ET-LBP, which overcomes the deviation of the extension state estimation in the ET-BP algorithm.Firstly, we formulate the data association problem in METT based on a new graphical model. Then, the graphical model is solved by the LBP algorithm to obtain the marginal PDFs of the joint posterior PDFs. In order to implement the ETLBP algorithm with high efficiency and accuracy,an improved scheme to the SMS is proposed.Finally,the simulation results show that the ET-LBP algorithm is superior to the ET-BP and Joint Probabilistic Data Association based on the SMS(JPDA-SMS) algorithms.20The Improved SMS (ISMS) has better performance than the SMS in tracking.

The rest of this paper is organized as follows. In Section 2,the basic assumptions, the factor graphs and the LBP algorithm are reviewed. Then, the data association problem in METT, the ET-LBP algorithm and the ISMS are proposed in Section 3. Section 4 illustrates the simulation results, and conclusions are given in Section 5.

2. Backgrounds

In this section, the underlying assumptions of METT are reviewed in Section 2.1, and the factor graphs and the LBP algorithm are introduced in Section 2.2.

2.1. Basic assumptions

Table 1 Bayesian framework.

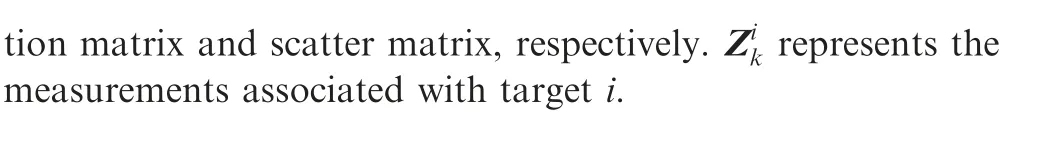
2.2. Factor graphs and LBP

The factor graph27is a graphical model,consisting of variable nodes and factor nodes, in which the variable nodes represent random variables and the factor nodes describe the dependencies between the random variables. The graphical models also include undirected graphical models(Markov random fields)28and directed graphical models(Bayesian networks).29In a factor graph, if some variables are dependent on each other in a factor node, then the variable nodes and the factor node are adjacent,connected by edges.For example,suppose that a factor graph includes variable nodes n ∈N and factor nodes f ∈F with neighbor nodes vf, where N and F represent all the variable nodes and factor nodes in the factor graph, respectively.The joint PDF f x( ) can be factorized as

where ψ(·) and φ(·) are the PDFs of variables and factors,respectively.

Then,the BP algorithm is able to marginalize the joint PDF f(x )by calculating the marginal PDFs f (xn)with a small computational cost.The BP is a message passing algorithm,which calculates messages of each variable node, and messages passing between variable nodes and factor nodes.The message sent from variable node xnto factor node f is given by

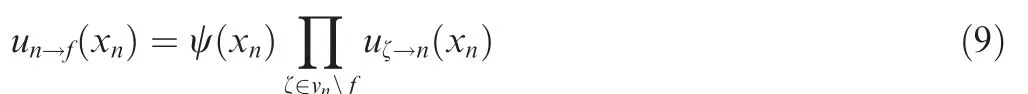
It is worth noting that the BP algorithm becomes the LBP algorithm if it is applied to a factor graph with loops.The LBP algorithm performs iteratively, in which the entire message update process is repeated several times. Additionally, the LBP algorithm can be interpreted as a variational algorithm that aims to solve a constrained optimization problem.30Although the optimization problem is not convex, the marginal PDF obtained by the LBP algorithm has been shown with reasonable accuracy in many applications.31,32The LBP algorithm can also approximate the marginal PDFs well when the optimization problem is locally convex, and the starting point can be obtained in the region. Thus, if the optimization problem is constructed as convex,33the global optimum can be obtained by the resulting iterative message passing algorithm.Although they can result in more accurate marginal PDFs than using the LBP algorithm directly,the computational complexity becomes higher.

3. Proposed algorithm

In this section, the data association problem in METT is formulated in Section 3.1. Then, the ET-LBP algorithm is proposed to solve the data association problem in Section 3.2.Furthermore, the difference between the ET-LBP and ET-BP algorithms is analyzed in Section 3.3.At the same time,a tractable implementation of the ET-LBP algorithm is presented by improving the SMS in Section 3.4.

3.1. Data association in METT

3.2. LBP based extended target tracking

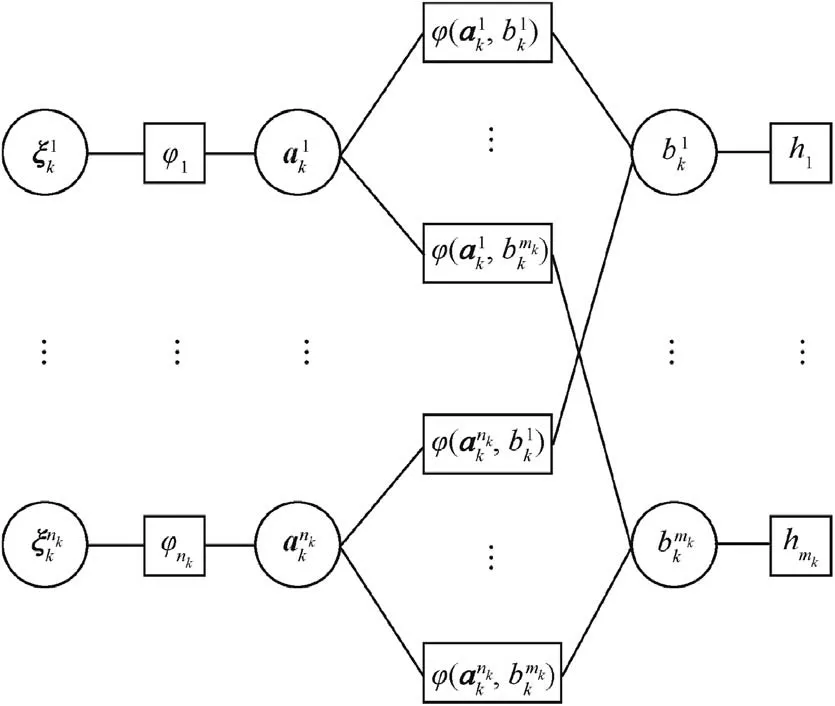
Fig. 1 Factor graph for data association problem in METT.

3.3. Difference between ET-LBP and ET-BP

3.4. Improved SMS

It has been shown that the measurement Zkcan be approximated by the SMS based on Minimal Spanning Tree (MST)algorithm20. The measurements, close to each other, are considered as generating from the same extended target in the SMS. Simulations based on random matrices show that the SMS is insufficient when some extended targets are close in space. This phenomenon is similar to the insufficiency of distance partition5. The SMS with thresholds cannot distinguish measurements of two extended targets well when they are close in space.It may result in aikwith too many or too less measurements.Thus,the wrong measurement association may cause a significant error in extension state estimation.

Fig.2 explains phenomenon using an example.In Fig.2(a),two extended targets are denoted in solid ellipses,and the measurements of these two extended targets are denoted in points.The SMS with threshold is shown in Fig.2(b),where measurement cells are denoted in dotted ellipses.It can be seen that the left measurement cell contains measurements of the right extended target. The reason for this is that several measurements of the right target are close to the left target. Consequently, the left measurement cell is with too many measurements, and the right measurement cell is with too few measurements.

In order to handle this phenomenon, an Improved SMS(ISMS) is proposed based on the prediction information. On

3.4.2. Subpartition

When targets are close in space, there may exist measurement cells with too many measurements in the SMS with thresholds.20This is because measurements from more than one target will be assigned to the same measurement cell. Such measurement cells would make some targets associate with too many measurements. Therefore, the tracking accuracy is poor in this situation.A subpartition algorithm6has been proposed based on K-means clustering.It can split these measurement cells,with too many measurements, into smaller cells.In order to avoid such a situation in the SMS,measurement cells generated by subpartition are added into the SMS.

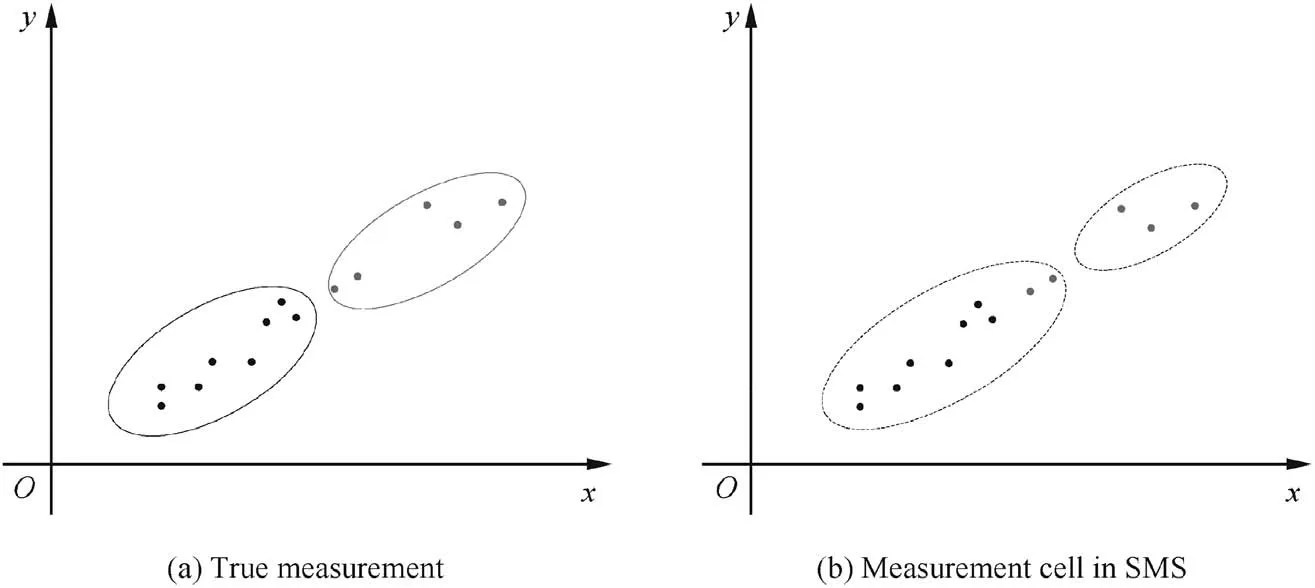
Fig. 2 Factor graph for data association problem in METT.

Table 2 Computing the K best associations of target i

Remark. The ISMS is composed of three parts, including the measurement cells from the SMS, the K best associations and the subpartition. It is worth noting that using all these three parts in this work is essential.The SMS contains measurement cells, which are most likely generated from extended targets.Because the SMS is not accurate when targets are close in space, the measurement cells from the K best associations and the subpartition are needed. Besides, the K best associations rely on prediction information. It may return non-informative measurement cells when targets are maneuvering. Thus,only the measurement cells from the K best associations are not enough. For this reason, it is better to use all these three parts.

4. Simulations

In this section, the ET-LBP algorithm is compared with the algorithms20based on the SMS, named ET-BP-SMS and JPDA-SMS. In order to verify the effectiveness of the proposed algorithm, the SMS20and the ISMS in Section 3.4 are used in the proposed algorithm, named ET-LBP-SMS and ET-LBP-ISMS, respectively.

4.1. Parameter setting

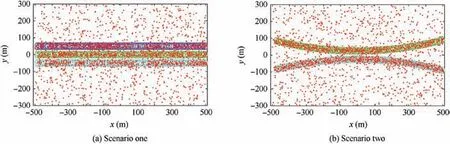
Fig. 3 True target trajectories when PD =0.99.

4.2. Simulation results

4.2.1. Scenario one

The simulations are performed by MATLAB R2015b on PC with Intel Core i3-7100 3.90 GHz processor and 8 GB RAM.The proposed algorithm is simulated in terms of tracking accuracy, computational efficiency and convergence.

In case of PD=0.99, the TSRs of the ET-LBP-ISMS, ETLBP-SMS, ET-BP-SMS and JPDA-SMS algorithms are 97.4%, 96.2%, 96.4% and 94.6%, respectively. It can be seen that the ET-LBP-ISMS algorithm is better than the other algorithms in TSR, and that the ET-LBP-SMS and ET-BP-SMS algorithms almost have the same performance. The position error and extension error of these algorithms are shown in Fig. 4 when PD=0.99. From Fig. 4(a), it can be seen that the ET-LBP-ISMS algorithm has a smaller error in position estimation. The reason for this is that the ISMS considers the prediction information and includes the subpartition operation. The ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms are all based on the SMS. Although the ET-LBPSMS algorithm almost has the same performance with the ET-BP-SMS and the JPDA-SMS algorithms in position estimation, it has a more accurate extension state estimation, as seen in Fig. 4(b). The main flaw of the ET-BP-SMS algorithm is the deviation in extension state estimation, compared with the JPDA-SMS algorithm. Thus, the ET-LBP-SMS algorithm overcomes the flaw in the ET-BP-SMS algorithm with better efficiency, which is consistent with the analysis results in Section 3.3.1.

In case of PD=0.80, the TSRs of the ET-LBP-ISMS, ETLBP-SMS, ET-BP-SMS and JPDA-SMS algorithms are 96.0%, 94.4%, 95.6% and 91.6%, respectively. The position error and extension error of these algorithms are shown in Fig.5 when PD=0.80.Although all these algorithms have larger errors in position and extension state estimation with lower PD, they can track targets well. Therefore, the proposed algorithms are robust to lower PD.

Simulations show that the performance of the ET-BP-SMS algorithm is sensitive to the upper probability and lower probability. In the precious algorithm,20the upper probability and lower probability are set to be 0.6 and 0.4, respectively. Thus,the number of measurement cells in the SMS is small, and the run time of the ET-BP-SMS algorithm is shorter. The SMS used in this paper contains more measurement cells.The extension error becomes larger in this paper because the wrong measurement cells in the new measurement cells influence the performance of the ET-BP-SMS algorithm.It can be seen that the ET-LBP-SMS algorithm is more robust to the upper probability and lower probability of the SMS.

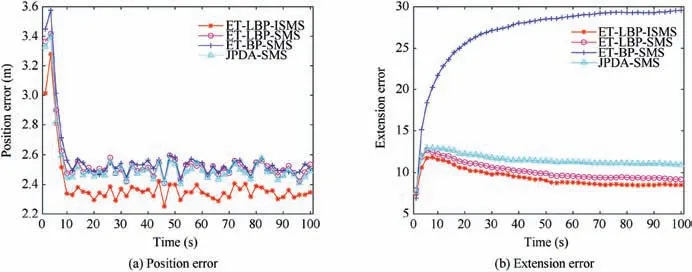
Fig. 4 Position error and extension error of ET-LBP-ISMS, ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms in scenario one when PD =0.99.

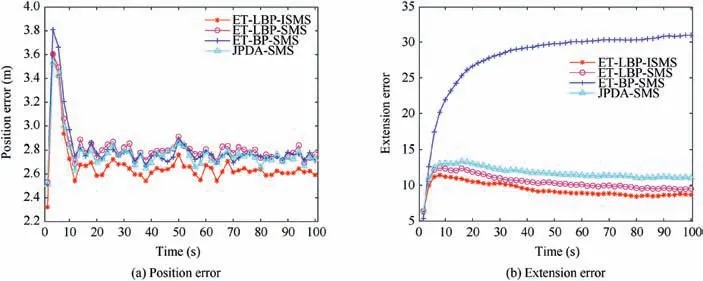
Fig. 5 Position error and extension error of ET-LBP-ISMS, ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms in scenario one when PD =0.80.

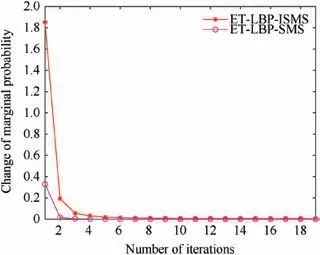
Fig. 6 Convergence of ET-LBP-ISMS and ET-LBP-ISMS algorithms.

The average run time of each time step of the ET-LBPISMS, ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms are 0.143 s, 0.080 s, 0.258 s and 2.215 s, respectively,when PD=0.99. It can be seen that the ET-LBP-ISMS and ET-LBP-SMS algorithms are more efficient. The average run time of each time step of the ET-LBP-ISMS algorithm is longer than that of the ET-LBP-SMS algorithm. The reason for this is that more measurement cells in the ISMS increase the computational complexity in the LBP algorithm. It can also be seen that the ET-LBP algorithm significantly improves the efficiency of the ET-BP when the average time of ET-LBPSMS and ET-BP-SMS algorithms are compared. The simulation results are consistent with the complexity analysis results mentioned above.

In the LBP algorithm, an iteration terminates when the marginal posterior distribution does not change anymore or the number of iterations exceeds the maximum number of iterations.The change of marginal posterior distribution is evaluated by summing the difference between marginal posterior distributions in adjacent iterations. In order to analyze the scalability of the ET-LBP-ISMS and ET-LBP-SMS algorithms, Fig. 6 shows the average difference in marginal posterior distributions during iteration with PD=0.99. It can be seen that these two algorithms both have good convergence.They can almost reach convergence after the 8th iteration.

4.2.2. Scenario two

In case of PD=0.99, the TSRs of the ET-LBP-ISMS, ETLBP-SMS, ET-BP-SMS and JPDA-SMS algorithms are 100%, 99.6%, 99.8% and 99.4%, respectively. It can be seen that the ET-LBP-ISMS algorithm is slightly better than the other algorithms in TSR. The position error and extension error of these algorithms are shown in Fig. 7 when PD=0.99. From Fig. 7(a), when targets are distant in space,it can be seen that these algorithms all perform well, and the ET-LBP algorithm has a smaller error in position estimation than the ET-BP algorithm. When targets are close in space,the ET-LBP-ISMS algorithm has a smaller error than the other algorithms in position estimation. Although the ETLBP-SMS algorithm almost has the same performance with the JPDA-SMS algorithm in position estimation, it has more accurate extension state estimation, as shown in Fig. 7(b).Thus, compared with the ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms, the ET-LBP-ISMS algorithm is more robust when targets are close in space.

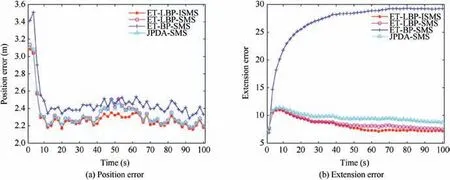
Fig. 7 Position error and extension error of ET-LBP-ISMS, ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms in scenario two when PD =0.99.

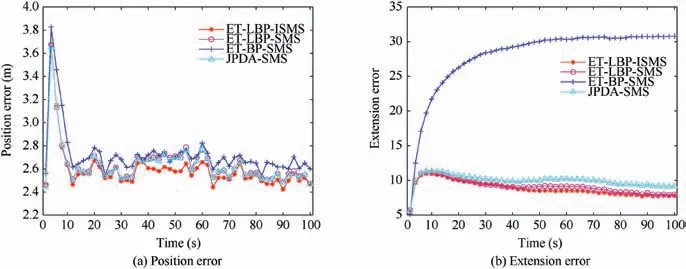
Fig. 8 Position error and extension error of ET-LBP-ISMS, ET-LBP-SMS, ET-BP-SMS and JPDA-SMS algorithms in scenario one when PD =0.80.

In case of PD=0.80, the TSRs of the ET-LBP-ISMS, ETLBP-SMS, ET-BP-SMS and JPDA-SMS algorithms are 96.8%, 94.8%, 96.8% and 93.6%, respectively. The position error and extension error of these algorithms are shown in Fig. 8 when PD=0.80. Although all these algorithms have more significant errors in position and extension state estimation with lower PD,they can all track targets well.The average run time of each time step of the ET-LBP-ISMS, ET-LBPSMS, ET-BP-SMS and JPDA-SMS algorithms are 0.073 s,0.050 s, 0.162 s and 0.075 s, respectively, when PD=0.99. It can also be seen that the ET-LBP-ISMS and ET-LBP-SMS algorithms are more efficient.

5. Conclusions

A new METT algorithm is proposed in this paper,named ETLBP-ISMS. The algorithm is based on the graphical model with loops,which is solved by the LBP algorithm.At the same time,the ISMS is presented by adding some new measurement cells into the SMS.Based on Murty’s algorithm35and the prediction information, these new measurement cells contain the K best associations for each target and the subpartition of big measurement cells. Simulations show that the ET-LBP algorithm has better accuracy than the ET-BP algorithm in terms of extension state estimation when they are implemented on the SMS. At the same time, the ET-LBP-ISMS algorithm has better performance in the kinematic state and extension state estimation. Therefore, the LBP algorithm can solve the data association problem of extended target tracking efficiently. Besides, although the RFS based algorithms avoid the data association problem, they still suffer from high computational complexity, especially in METT. Thus, researching more efficient METT algorithms based on RFS is also our future direction.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 61871301), National Natural Science Foundation of Shaanxi Province, China (No.2018JQ6059) and Postdoctoral Science Foundation of China(No. 2018M633470).