基于双齿面传动误差的侧隙连续测量与预测
王光建,周 磊,邹帅东
1) 重庆大学机械传动国家重点实验室,重庆 400044 2) 重庆大学汽车工程学院,重庆 400044 3) 重庆大学机械工程学院,重庆 400044
齿轮传动误差和侧隙是影响精密传动系统运动准确性的重要因素,而由于加工、装配等导致的偏心误差(包括轴、齿轮、轴承等制造及装配误差)是大周期传动误差和周期性侧隙的主要来源[1−3].因此有必要分析研究偏心误差作用下的齿轮传动误差和侧隙.
国内外学者对齿轮系统传动误差进行了较多研究. 文献[4]按照传动比的高和低,分别用两种不同的计算公式对误差进行相位补偿,文献[5]~[6]指出其不足并在其基础上采用解析法推导出偏心误差的齿轮副传动误差公式. 由于解析法求解过程复杂,啮合线增量法计算传动误差较为简单,应用更为普遍,如文献[1],文献[7]~[8]通过啮合线增量法分别计算了具有偏心误差的外啮合齿轮副,NGW行星减速器的传动误差. 而在高速轻载或交变负载力矩齿轮传动以及无隙啮合传动中,通常会出现轮齿齿背面啮合[9−13],但上述计算传动误差的文献中并未明确指出齿背面啮合传动误差计算方法,因此分析计算齿背面传动误差具有重要意义.
由于齿轮侧隙的强非线性,其直接影响伺服控制的稳定性、响应性、精度和系统敏感度[14];同时对于精密传动系统,特别在轻载高速工况下,侧隙也是影响齿轮动态特性的重要因素[15−19]. 因此通过测量获得全面的齿轮侧隙数据具有重要意义. 而目前齿轮侧隙的测量方法[20]主要包括塞尺法、百分表法、度盘法、自整角机法和机械滞后回差法等,测试数据离散,数据不全面,效率较低.
本文提出一种基于双齿面传动误差的侧隙连续测量新方法. 通过建立双面传动误差计算模型,建立与侧隙计算公式等价关系. 并通过实验方法得到不同负载力矩下的双齿面动态传动误差曲线,推导由变形引起的回差与负载力矩的关系,从而得到无负载双齿面传动误差曲线,最终获得连续侧隙曲线. 同时根据齿背面传动误差曲线及其理论模型,拟合得到齿轮副偏心误差及初始相位,实现对整个大周期侧隙值的快速预测.
1 双面传动误差与侧隙理论模型
1.1 双面无负载传动误差
定义因轴承、轴及齿轮等加工及装配误差导致主动轮几何中心与其实际旋转中心的偏移量e1为主动轮综合偏心误差,见图1,则当轮齿啮合面为驱动齿面时,其啮合线增量计算如下,
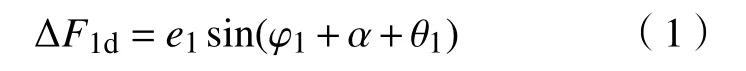
当轮齿啮合面为齿背面时,其啮合线增量为,

式中: ∆F1(包括 ∆F1d和 ∆F1b)为主动轮偏心导致的啮合线增量; φ1为主动轮任意时刻的转动角位移;e1和 θ1为主动轮偏心误差及其初始相位;α为齿轮副压力角. 其中,定义与主动轮旋转方向一致的齿面为驱动齿面,与主动轮旋转方向相反的齿面为齿背面,如图1所示.
同理,定义从动轮几何中心与其实际旋转中心的偏移量e2为从动轮综合偏心误差,见图2,则当轮齿啮合面为驱动齿面时,其啮合线增量计算如下,

当轮齿啮合面为齿背面时,其啮合线增量为,

式中: ∆F2(包括 ∆F2d和 ∆F2b)为从动轮偏心导致的啮合线增量; φ2为从动轮任意时刻的转动角位移;e2和 θ2为从动轮偏心误差及其初始相位.

图1 主动轮偏心误差下啮合线增量计算模型. (a)啮合齿面为驱动齿面;(b)啮合齿面为齿背面Fig.1 Engagement increment calculation model with eccentric error of pinion:(a) drive-side meshing; (b) back-side meshing
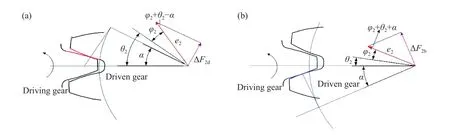
图2 从动轮偏心误差下啮合线增量计算模型. (a)啮合齿面为驱动齿面;(b)啮合齿面为齿背面Fig.2 Engagement increment calculation model with eccentric error of driven gear:(a) drive-side meshing; (b) back-side meshing
定义仅由偏心引起的传动误差为无负载传动误差(后面实验研究的由偏心误差、刚度、负载及时变侧隙引起的传动误差定义为动态传动误差),将啮合齿面不同情况下的主从动轮啮合线增量转化为从动轮旋转角度,则可分别得到驱动齿面与齿背面无负载传动误差.
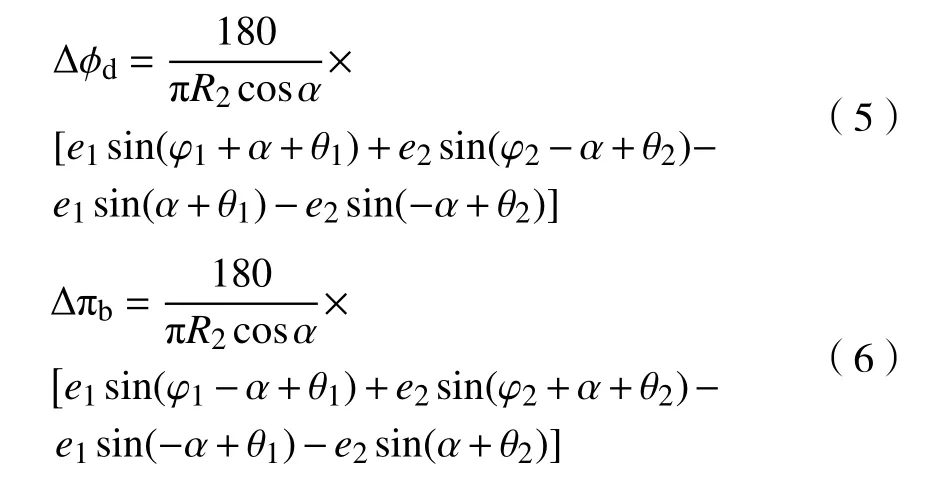
式中: ∆ ϕd为驱动齿面啮合时无负载传动误差;∆ϕb为齿背面啮合时无负载传动误差,单位均为度(°);R2为从动轮分度圆半径.
1.2 侧隙理论计算模型
齿轮传动的侧隙通常包括常值侧隙和周期性变值侧隙[21],其中常值侧隙主要由齿厚偏差、中心距误差等引起;周期性变值侧隙主要由轴承、轴及齿轮等制造、装配偏心误差引起. 周期性变值侧隙计算如下:

将上式用牛顿二项式定理展开,得,

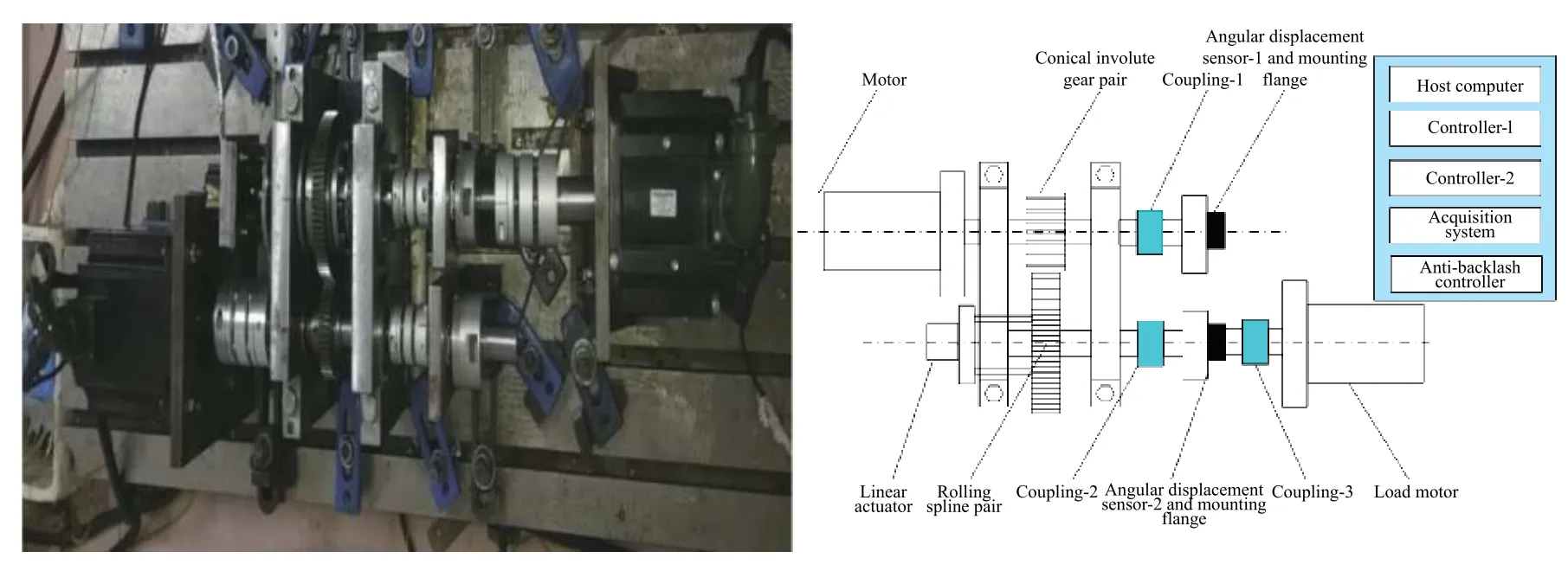
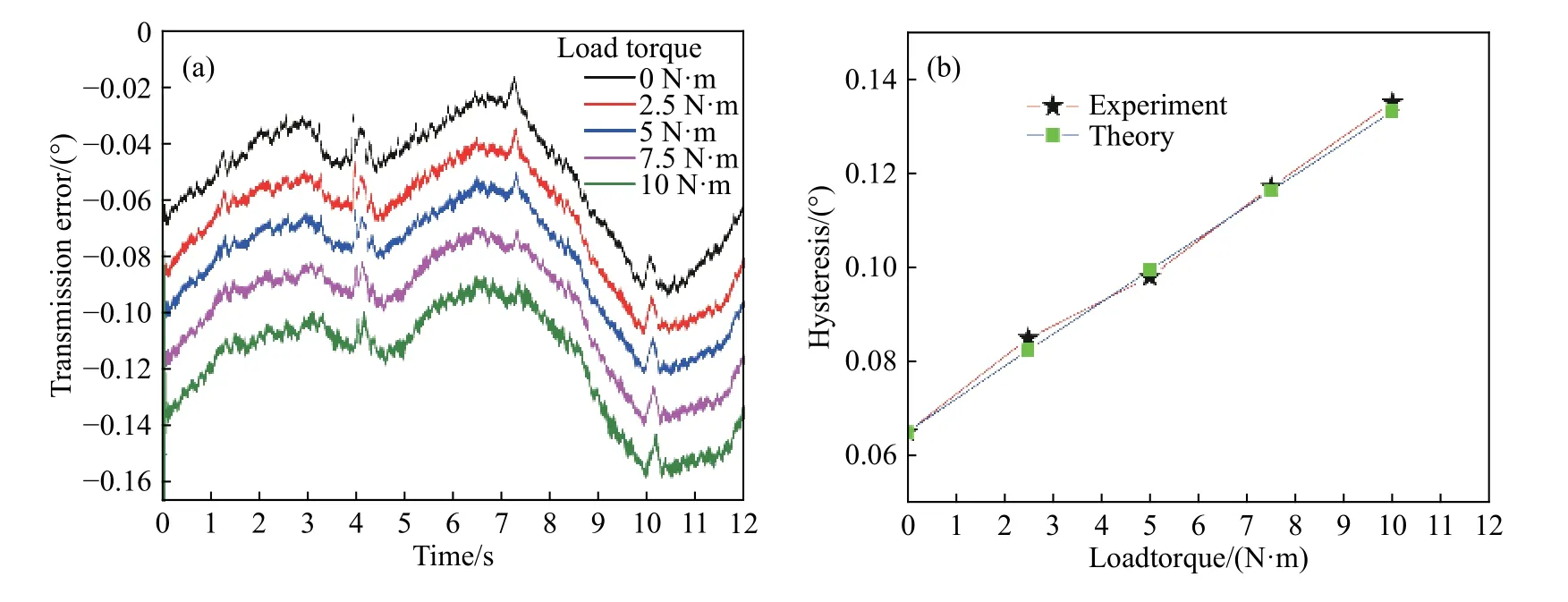
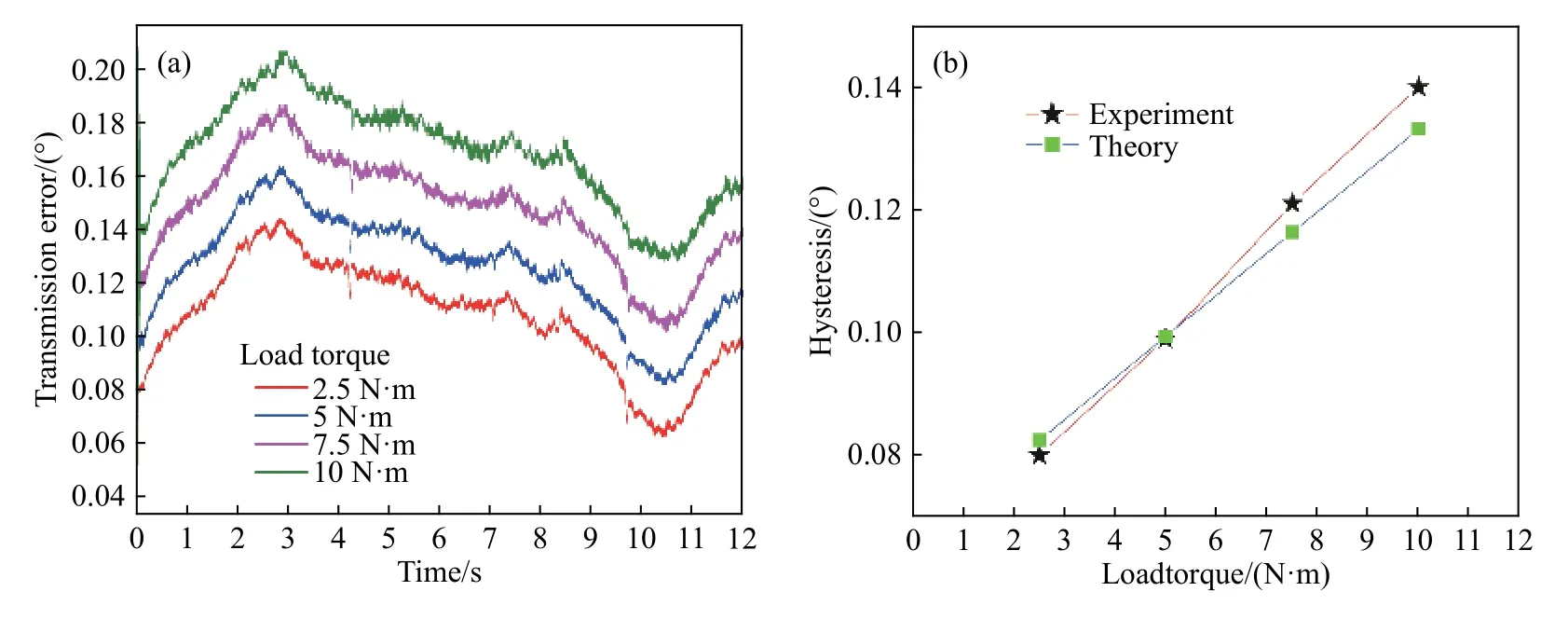
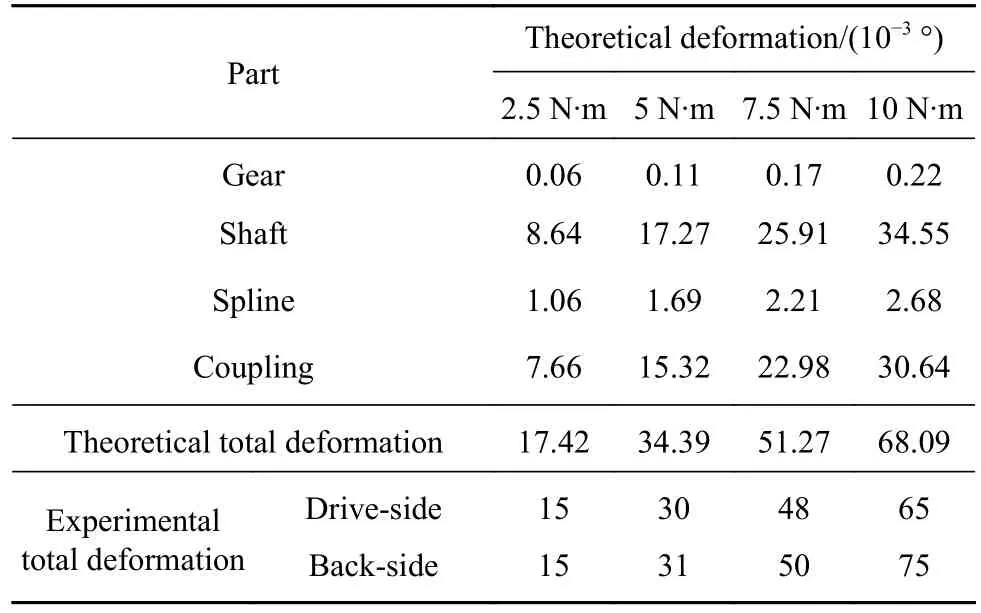
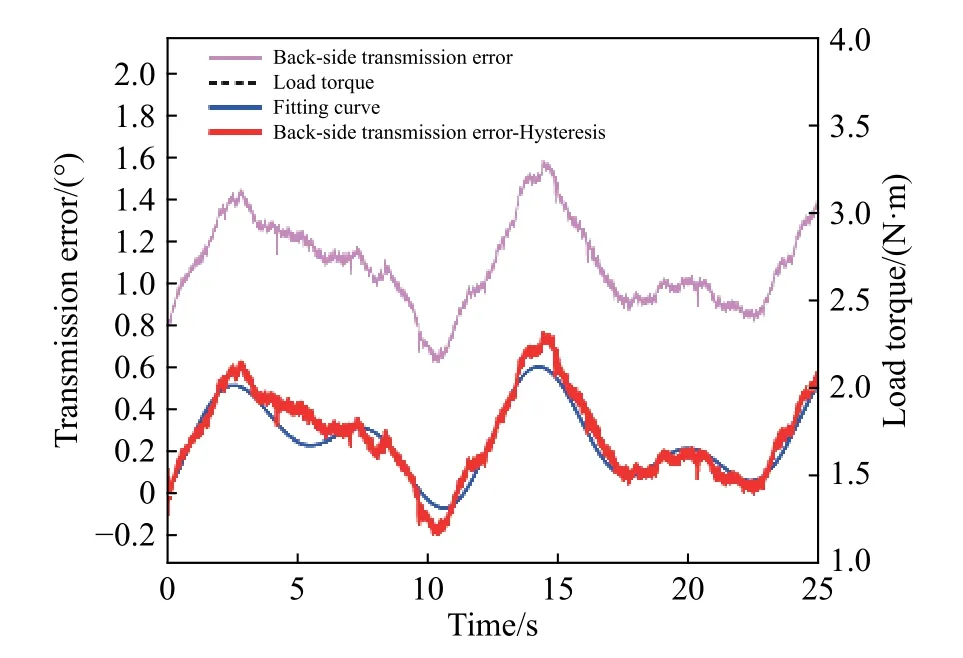
其中,a为齿轮副安装中心距,由于e1< 由公式(9)易知初始变值侧隙为, 因此,齿轮副总侧隙及初始总侧隙可表示为, 式中:jv、jv0、jφ、jφ0及jc分别为齿轮副变值侧隙,初始变值侧隙,总侧隙,初始总侧隙及常值侧隙,单位均为度(°). 通过前文计算公式可知, 由上式可知,齿轮副侧隙可间接通过驱动齿面无负载传动误差及含初始侧隙的齿背面无负载传动误差得到. 实验装置如图3,实验系统包括驱动电机、变齿厚齿轮副、编码器、负载电机、滚珠花键副、数据采集系统、电机的控制器、直线执行器、消隙控制器以及上位机等. 通过控制器1控制驱动电机旋转,控制器2控制负载电机提供实验所需负载,主从动轮转动角度分别通过编码器1和2测量,测量的角位移数据由数据采集系统采集并带入公式(14)计算,从而获得双齿面实验传动误差曲线. 由于本实验仅涉及传动误差及侧隙测量,并未涉及消隙实验,因此消隙控制器及直线执行器未使用,但连续侧隙的测试对消隙控制研究具有重要意义[22−24].此外,本装置中的变齿厚齿轮副属于渐开线齿轮副一种,因此上述建立的传动误差及侧隙理论模型仍然适用. 实验参数及齿轮副参数如表1. 式中,∆ ϕ为传动误差,φ2s分别为编码器2测量角位移,φ1s为 编码器1测量角位移,i为传动比. 当驱动电机驱动主动齿轮旋转,其方向与负载力矩方向均为逆时针时,若启动时开始接触齿面为驱动齿面,如图4(a),实验所测的传动误差曲线为初始无侧隙驱动齿面传动误差;若启动时开始接触齿面为齿背面,如图4(b),则实验所测的传动误差曲线为含初始侧隙的驱动齿面传动误差.当驱动电机驱动主动齿轮逆时针旋转,负载力矩方向为顺时针方向时,若启动时开始接触齿面为驱动齿面,如图5(a),实验所测的传动误差曲线为含初始侧隙的齿背面传动误差;若启动时开始接触齿面为齿背面,如图5(b),则实验所测的传动误差曲线为初始无侧隙齿背面传动误差. 由于主从动轮齿数的关系,当主动轮旋转16圈,从动轮旋转9圈时,齿轮啮合的轮齿相同,齿轮副回到初始测试起点. 为方便进行实验结果比较,主动轮每次均由相同起始位置开始,起始位置的精度由编码器保证. 实验中为保证实验数据的可靠性,每组数据均进行重复性实验. 按图4~图5所示初始位置,分别进行不同负载力矩下的双齿面传动误差曲线测量,实验结果如图6~图9. 定义回差为负载下实验装置的变形与齿轮副侧隙值之和,即 式中,B为回差,∆ δk为负载引起的变形. 因此,初始时刻的回差(以下简称初始回差)为负载引起的变形和齿轮副初始侧隙之和,即 式中,B0为初始回差 由实验装置图3可知,负载引起的变形和齿轮副初始侧隙为编码器2在初始时刻测量所得角度值的绝对值,而初始时刻编码器1测量角度值因此, 式中,B0为初始回差,∆ ϕ0为传动误差初始值. 图3 传动误差及侧隙测量实验装置图Fig.3 Experimental device for transmission error and backlash measurement 表1 齿轮副基本参数Table 1 Basic parameters of gear pair 由公式(17)知,初始回差即为初始时刻传动误差值绝对值. 图6(a)中为不同负载的驱动齿面传动误差曲线,同时由于初始接触齿面为驱动齿面,即齿轮副初始侧隙为零,联立公式(16)及(17)可知,传动误差曲线的初始时刻值的绝对值(即初始回差)等于负载引起的变形值. 当负载力矩为零时,负载引起的变形为零,因此传动误差曲线初始时刻值为零. 而随着负载力矩逐渐增加,导致齿轮、轴、联轴器等零件变形加大,初始回差逐渐增大,因此传动误差曲线初始时刻值的绝对值逐渐增大,即逐渐远离坐标原点. 由各负载下传动误差初始时刻值及公式(17)可得相应负载下的初始回差实验值,如图6(b)所示,而初始回差理论值由计算所得,将在 2.4节具体阐述. 此外,从图 6(b)可知,负载力矩与初始回差呈较好的线性关系. 图7(a)所示,由于初始接触齿面发生变化,齿轮副初始侧隙值不为零,因此,传动误差曲线初始时刻为初始侧隙值与负载引起的变形值之和. 当负载为零时,负载引起的变形为零,因此由公式(16)及公式(17)可知,传动误差初始时刻值的绝对值即为齿轮副初始侧隙,即约为0.065°. 同时由各负载下传动误差初始时刻值及公式(17)可得相应负载下的初始回差实验值,如图 7(b)所示. 图 7(b)中,初始回差与负载也呈较好的线性关系. 同理可分析图8与图9齿背面传动误差曲线与初始回差. 图8(a)中,当初始时刻接触面为驱动齿面时,齿轮副初始侧隙不为零,初始回差为齿轮副初始侧隙及实验装置变形之和;图9(a)中,当初始时刻接触面为齿背面时,齿轮副初始侧隙为零,因此初始回差等于实验装置变形. 此外,如图8(b)与9(b)所示,初始回差与负载也呈较好的线性关系,且变化斜率基本与图 6(b)、图 7(b)一致. 图4 驱动齿面传动误差测量起始位置示意图. (a)初始接触齿面为驱动齿面;(b)初始接触齿面为齿背面Fig.4 Schematic of the initial position of the drive-side transmission error measurement:(a) drive-side contact in initial position; (b) back-side contact in initial position 图5 齿背面传动误差测量起始位置示意图. (a)初始接触齿面为驱动齿面;(b)初始接触齿面为齿背面Fig.5 Schematic of the initial position of the back-side transmission error measurement:(a) drive-side contact in initial position; (b) back-side contact in initial position 图6 驱动齿面传动误差测量且初始时刻驱动齿面接触. (a)传动误差对比曲线;(b)各负载与其初始回差对比Fig.6 Drive-side transmission error measurement with drive-side contact at initial position:(a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis 图7 驱动齿面传动误差测量且初始时刻齿背面接触. (a)传动误差对比曲线;(b)各负载与其初始回差对比Fig.7 Drive-side transmission error measurement with back-side contact at initial position:(a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis 图8 齿背面传动误差测量且初始时刻驱动齿面接触. (a)传动误差对比曲线;(b)各负载与其初始回差对比Fig.8 Back-side transmission error measurement with drive-side contact at initial position:(a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis 从图3实验装置图可知,当施加负载力矩时,编码器2测量的角度中包含的变形主要是齿轮副变形、滚珠花键副变形、膜片联轴器2变形及从动轮至编码器2之间的输出轴变形. 因此总变形可以表示下, 图9 齿背面传动误差测量且初始时刻齿背面接触. (a)传动误差对比曲线;(b)各负载与其初始回差对比Fig.9 Back-side transmission error measurement with back-side contact at initial position:(a) comparison of transmission error curves; (b) comparison of each load torque with its corresponding hysteresis. 式中,T为负载力矩,kg、ka、ks及kc分别为单位宽度齿轮副刚度、从动轮至编码器2之间的输出轴刚度、滚珠花键副刚度及联轴器刚度. 其中,单位宽度齿轮副刚度通过文献 [20]查得为 20 N·(μm·mm)−1,轴的刚度由文献 [25]得 289.44 N∙m·(°)−1,滚珠花键副刚度参考文献 [26]计算后为 9.768×107·P1/3N·m−1,其中P为外载作用力,膜片联轴器刚度参考文献[25]为 1.87×104N∙m·rad−1. 各部分刚度及变形如表 2、表3所示. 表2 各部分理论刚度Table 2 Theoretical stiffness of each part 表3 不同负载力矩下,各部分变形数据Table 3 Deformation data of various parts under different loads 从表3可以看出,各负载力矩下实验总变形结果与理论结果吻合较好,且引起变形回差的主要因素是轴和联轴器. 由公式(16)可知,初始回差主要由实验装置变形和齿轮副初始侧隙组成,因此变形越大,初始回差越大. 同时表2中,轴与联轴器刚度相对较低,即变形较大,因此对初始回差影响较大. 联立公式(16)及(18)得 由公式(19)可知,初始回差与负载之间理论上呈线性关系. 将表3中各负载下计算的理论变形值以及2.3节的齿轮副初始侧隙值代入公式(16),得到理论初始回差,如图 6(b)、图 7(b)、图 8(b)及图 9(b). 由图 6(b)~图 9(b)可知,实验和理论初始回差吻合较好,且均与负载具有较好的线性关系. 当通过公式(13)获得齿轮副连续侧隙曲线时,双齿面传动误差曲线必须为无负载传动误差曲线. 由图 6(a)~图 9(a)可知,负载下的传动误差曲线与无负载下的传动误差曲线为常值的上下偏移,其偏移值与表3中计算的变形值相等,即 图10 双面传动误差与侧隙连续曲线Fig.10 Two-sided transmission error and continuous backlash curve 3.2.1 初始侧隙、偏心误差及其初始相位预测 不同于上述侧隙连续测量方法,侧隙预测只需采集一段含初始侧隙的齿背面传动误差曲线,以2.5 N∙m含初始侧隙的驱动面传动误差实验曲线为例,如图11,易知初始回差为0.08°,除去负载力矩引起的理论变形量0.015°(第2部分刚度计算中已求),因此齿轮副初始侧隙jφ0为0.065°. 再将不含初始回差的齿背面传动误差曲线带入其理论模型公式(6),通过实验数据拟合,从而预测出齿轮副的偏心误差及其初始相位,拟合曲线如图11,拟合得到偏心误差和初始相位分别为:e1=0.023 mm,θ1= −12.9◦,e2=0.026 mm,θ2= −69.8◦. 图11 齿背面传动误差实验及拟合曲线Fig.11 Experimental and fitting curve of back-side transmission error 3.2.2 变值侧隙、常值侧隙及总侧隙预测 将拟合得到的偏心误差及初始相位带入侧隙模型公式(9)得到变值侧隙,如图12. 再通过公式(10),得初始变值侧隙jv0为−0.007°,并由初始侧隙和初始变值侧隙值,通过公式(12)得常值侧隙为0.072°,最后得到齿轮副总侧隙,如图12所示. 图12 侧隙预测曲线Fig.12 Predicted backlash curve 如图13所示,机械滞后回差测量法是将主动轮固定,再将从动轮分别转动到驱动齿面接触和齿背面接触两个位置,记录两个位置的角度值并相减,并除去该力矩下引起的变形角度,从而得到该位置处齿轮副的侧隙值. 再将主动转动一定角度,重复上面操作,从而得到一组离散的侧隙值曲线. 本实验在一个大周期内(主动轮16圈,从动轮9圈)以及 2.5 N∙m 负载力矩下,主动轮从 0°到 5760°每旋转90°测试一组侧隙值,共计65组侧隙数据,测量结果如图14. 图13 机械滞后回差法测量原理Fig.13 Measurement principle of mechanical return backlash method 图14为三种侧隙测量方法测试结果,可以看出侧隙连续测量与机械滞后回差法测量的结果十分吻合,证明了基于双齿面传动误差的侧隙测量方法的正确性. 三种方法中,机械滞后回差法数据零散且不全面,且耗费时间周期长,效率低;基于双齿面传动误差的侧隙连续测量方法不需要单点进行测量,可以获得更全面的侧隙数据,且整个大周期侧隙结果仅在几分钟内便可全部得到,效率较高;侧隙预测方法效率最高,仅需测量一小段含侧隙的齿背面传动误差而得到整个大周期侧隙结果,但与其余两种方法相比,其结果存在有一定偏差,因为拟合得到的偏心误差与其初始相位以及计算的理论刚度值均与实际情况存在偏差,因此此方法只能大致预测侧隙值范围以及侧隙在整个大周期内的变化趋势. 图14 三种侧隙测量方法对比Fig.14 Comparison of three backlash measurement methods (1)本文建立双齿面传动误差及侧隙理论模型并建立三者等价关系. 进行了不同负载力矩下双齿面传动误差的测量. 结果表明负载力矩与初始回差呈较好的线性关系,负载力矩越大,变形越大,初始回差越大. 经过刚度理论计算发现引起变形回差的主要部分为膜片联轴器与输出轴,齿轮和滚珠花键影响较小. (2)基于双齿面传动误差实验曲线,实现了对齿轮整个大周期侧隙的连续测量与预测. 结果表明,连续测量曲线与机械滞后回差法测量结果吻合良好,而侧隙预测较好地反应了侧隙值变化范围和变化趋势. 同时,测量连续测量方法及侧隙预测均证明了理论模型的正确性,提高了侧隙测量效率并获得了更全面的侧隙数据,为齿轮传动的非线性研究、消隙控制以及齿轮精度研究等奠定了基础.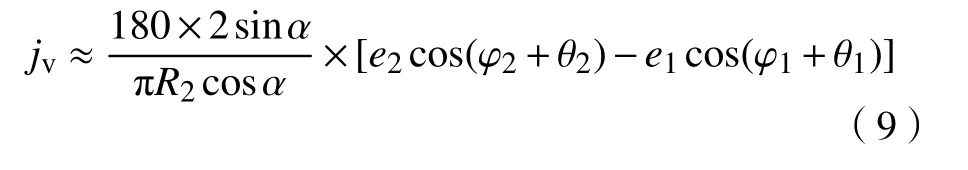


1.3 双齿面无负载传动误差与侧隙关系

2 双齿面传动误差测量
2.1 实验装置及参数

2.2 双齿面传动误差测量
2.3 传动误差实验曲线与初步分析


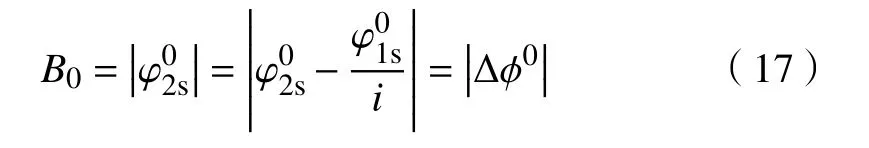




2.4 刚度计算与初始回差分析
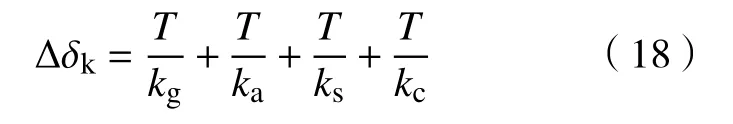



3 侧隙连续曲线与预测
3.1 侧隙连续曲线


3.2 侧隙预测

4 侧隙测量方法对比


5 结论

