基于多场耦合碳/碳复合材料传热及烧蚀响应

孙学文，杨海波，米 涛

1) 北京科技大学机械工程学院，北京 100083 2) 北京科技大学流体与材料相互作用教育部重点实验室，北京 100083

3) 东莞材料基因高等理工研究院，东莞 523808 4) 北华航天工业学院材料工程学院，廊坊 065000

随着高超声速技术的发展，飞行器服役环境越来越恶劣，对热防护材料提出了更高的要求[1−3].碳/碳复合材料具有较高的化学潜热，在高温环境下仍保持较高的强度，被广泛地应用于飞行器的热防护系统[4−6]. 飞行器服役过程中周围的热化学非平衡流场会影响碳/碳复合材料的传热及烧蚀，导致防热层的厚度和形状发生变化，材料烧蚀产物又与周围的高温气体发生化学反应，从而改变流场的温度及组元浓度等特性，流场特性的改变反过来又会影响飞行器防热层的烧蚀[7−10]. 因此，高超声速热化学非平衡流场与碳/碳复合材料之间存在着强烈的耦合作用，准确的预测碳/碳复合材料的内部温度分布以及烧蚀响应，对热防护系统的设计及优化具有重要的意义.

对热防护材料烧蚀性能的预测一直是发展高超声速飞行器所面临的关键问题之一，近年来国内外相关学者对其开展了一定的研究[11−13]. Martin与Boyd[14]建立了来流气体与热防护材料的耦合模型，主要分析了来流环境下热防护材料的温度响应以及防热材料烧蚀产物对外部流场的影响，并以IRV-2为计算模型对数值方法进行了验证.Cross与Boyd[15]针对火箭喷管环境下防热材料的响应进行研究，建立了喷管内流场与碳/酚醛材料的耦合反应模型，对喷管流场环境以及材料响应进行了研究. Mortensen与Zhong[16]针对防热材料表面烧蚀对高超声速边界层的影响，考虑了材料表面的烧蚀和真实气体效应，建立了流场的热化学非平衡模型，并以钝椎体为例进行验证，分析了表面烧蚀对高超声速边界层的影响. Chen等[17−18]针对碳化材料烧蚀响应预测，开发了全隐式的烧蚀热响应程序，用于模拟防热材料热解气体流动、热化学烧蚀以及外形变化等，最后采用三组算例对计算程序进行了验证. Kumar[19]建立了防热材料烧蚀与外部流场耦合的数值模型，重点分析了碳化材料热解过程，以及热解气体与外部流场之间的相互影响关系. Li等[20]针对碳化复合材料，建立了烧蚀面后退的非线性热解层模型，对其烧蚀响应进行预测. Candler等[21]针对碳基复合材料的氧化烧蚀过程，比较了有限速率反应模型以及化学平衡两种气−固反应模型对材料响应的预测，并采用球锥模型进行验证. Qin等[22]针对火箭发动机内部的热环境，建立碳/碳复合材料的多尺度热化学烧蚀模型，考虑基体及纤维的反应速率，对复合材料的烧蚀响应进行预测. Yin 等[23]，Meng 等[24]，Chen[25]考虑来流与固体材料的单向耦合作用，对碳/碳复合材料的烧蚀响应进行计算，预测烧蚀体的外形变化和温度分布等情况. 现有防热材料响应模型通常将气动热载荷直接作用于材料模型表面进行材料响应的单向耦合预测，未同时考虑由于材料温度及烧蚀外形变化等对外部流场的影响.

基于以上分析，本文在热化学烧蚀理论的基础上，采用流−热−烧蚀多场耦合策略，考虑外部流场热化学非平衡效应、材料传热以及表面烧蚀等因素，建立了碳/碳复合材料在高超声速环境下的双向耦合模型，对其传热及烧蚀响应进行预测，分析不同时刻材料模型的温度、烧蚀速率以及烧蚀外形的变化.

1 控制方程及多场耦合策略

碳/碳复合材料烧蚀过程的数值模拟需要考虑复杂的物理及化学过程，包括气动加热、表面烧蚀、材料热响应以及烧蚀边界移动等. 本文通过Fluent对外部流场进行建模计算，得到材料外部的气动热载荷，采用Abaqus计算材料的瞬态热响应，考虑有限速率烧蚀模型用来预测碳/碳复合材料的烧蚀后退，并用网格移动策略对烧蚀边界进行追踪，最后利用Mpcci实现流场与固体材料之间的数据传递.

1.1 外部流场控制方程

针对多组元的化学反应气体混合物，可压缩黏性热化学非平衡流动的Navier-Stokes控制方程组在直角坐标系中表达形式如下：

式中，Q为守恒变量，E、F分别为x、y方向的无黏通量，Ev、Fv分别为x、y方向的黏性通量，S为反应源项体现化学非平衡的影响.

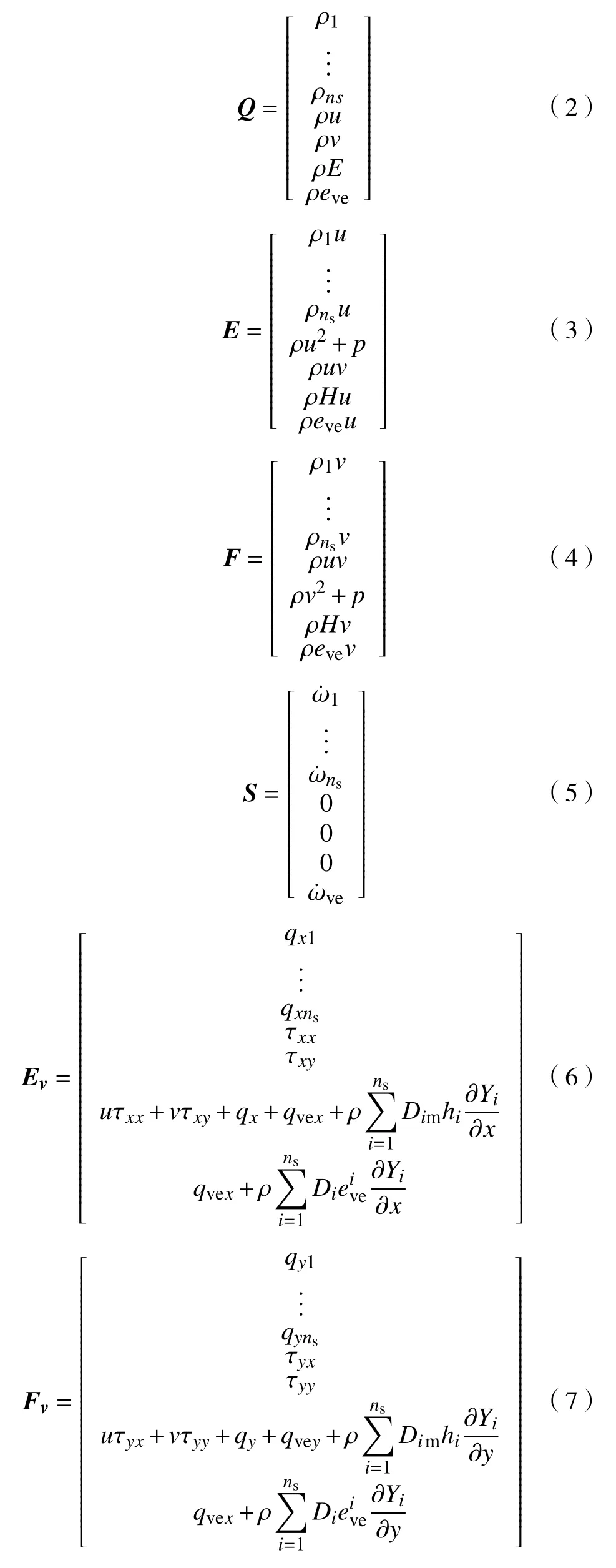
式中，u、v分别为x、y方向的运动速度，ρ、p分别为气体压力和密度，E、H为单位质量气体的总能量和总焓，ρi、i、Yi分别为气体组元i的密度、化学反应源项、质量分数，Dim、hi为 气体组元i的扩散系数和单位质量绝对焓，eve、ve表示单位质量气体的振动能及振动能源项，qx、qvex为气体在x方向的平动−转动热流和振动热流，qy、qvey为 气体在y方向的平动−转动热流和振动热流，τxx、τxy、τyy、τyx为剪切应力张量分量，ns为气体组元数量.

采用Gupta化学动力学模型计算化学反应引起的组元变化，具体化学反应模型见参考文献[26].

1.2 气−固界面及烧蚀速率模型

来流气体与固体材料之间需要满足能量守恒，图1为气−固界面能量传递示意，其满足关系式：

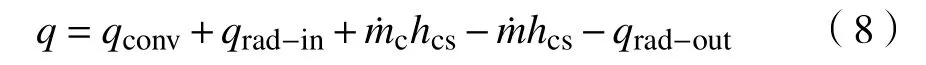
式中，q为 传入材料模型内部的热流，qconv为外部流场对材料壁面的气动加热热流，qrad−in为外部流场对材料的辐射加热量，chcs为壁面化学反应产生的热量，hcs为 烧蚀质量损失带走的热量，qrad−out为材料对外部流场的辐射散热量.

图1 气−固界面能量传递示意图Fig.1 Energy transfer at the gas−solid interface

采用有限速率烧蚀模型来模拟碳/碳复合材料的表面烧蚀，不考虑由于机械剥蚀及材料表面熔化等物理因素引起的质量损失，只考虑由于表面气固化学反应引起的质量变化.

碳/碳复合材料表面烧蚀主要包括碳的氧化和氮化，表面化学反应机制及质量损失率如下[24]：

（1）碳的氧化反应：O+Cs→CO

质量损失速率为：

（2）碳的氧化反应：O2+2Cs→2CO

质量损失速率为：

（3）碳的氮化反应：N+Cs→CN

质量损失速率为：

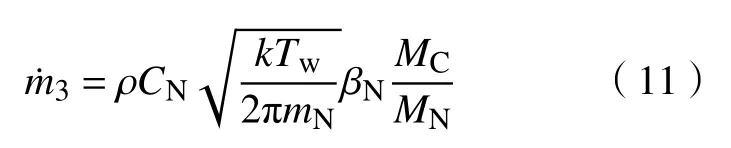
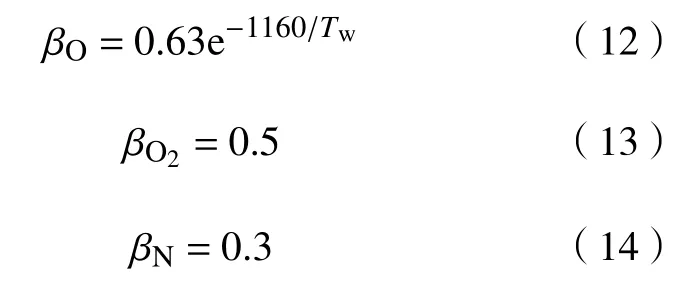
材料表面总的质量损失率为：

1.3 材料热响应模型及烧蚀边界追踪

固体材料的热传导会影响材料表面的温度分布、氧化属性以及烧蚀速率等，因此要准确预测材料的烧蚀响应，必须考虑材料热传导. 材料内部的热传导遵循傅里叶导热定律和能量守恒定律，材料内部热传导的控制方程在直角坐标系下可写为：

式中：t为时间，T为温度，ρs为 材料密度，cp为材料的定压比热容，λ为材料的热传导系数，q为施加在固体材料边界上的热载荷.

材料烧蚀为动态过程且烧蚀面不断发生变化，为准确预测烧蚀响应，需要捕捉烧蚀面的位置. 材料的烧蚀速率可按下式计算得到.

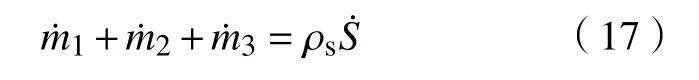
材料表面节点的移动通过烧蚀速率及时间步长 ∆t可计算得到，节点移动方向垂直于边界，节点移动位移为：

式中，δx、δy分别为烧蚀表面节点沿x、y方向的位移，nx、ny为烧蚀面的内法线在x、y方向的分量.

建模中通过Abaqus网格运动算法实现烧蚀表面后退的模拟，利用用户自定义接口函数Umeshmotion更新烧蚀表面节点位置. 网格节点的移动可能导致单元发生巨大变形，采用ALE（Arbitrary lagrangian-eulerian）网格自适应技术对模型内部网格进行重划分，进而避免网格的畸形，最终实现烧蚀表面后退过程的模拟.

1.4 流−热−烧蚀耦合分析策略

高超声速流动与材料的耦合建模采用分区法实现，根据物理空间分为流体部分和固体部分. 流体域与固体域的耦合实质是流体气动加热问题、固体内部热传导以及壁面烧蚀通过耦合界面发生相互作用的物理化学过程. 图2（a）中 Ωf和 Ωs分别为流体域和固体域，Γ为耦合界面，在耦合界面上，固体向流体提供壁面温度及位移边界，而流体向固体提供气动热载荷. 流场与材料模型的计算数据在耦合界面上反复交换，通过Mpcci实现两个区域非匹配网格间的数据传递，图2（b）为非匹配网格间的数据传递示意.

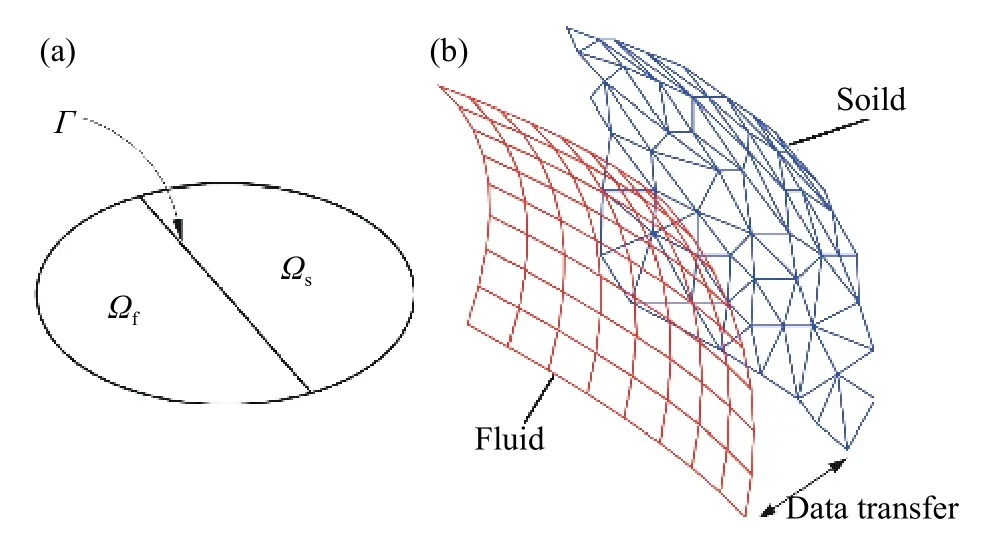
图2 流固耦合示意及界面数据传递. （a）流固耦合示意图；（b）非匹配网格间的数据传递Fig.2 Fluid structure coupling and data transfer at the interface:(a) fluid structure coupling; (b) data transfer between unmatched grids

图3 耦合计算流程Fig.3 Flow of coupled computing

流−热−烧蚀耦合分析的具体计算流程如图3所示. 首先计算热化学非平衡流场，获得壁面处的热流以及各化学组元的质量分数，然后以流场计算结果作为边界条件，进行材料内部传热和壁面烧蚀的计算，计算后将壁面温度、表面位置作为边界条件反馈回流场，并计算该时刻的流场分布情况. 通过耦合面数据的反复迭代，获得不同时刻材料温度及壁面烧蚀的分布情况.

2 碳/碳复合材料流−热−烧蚀耦合模型

对零攻角碳/碳复合材料前缘模型烧蚀性能进行数值计算. 该算例模型选自文献[24]，模型尺寸可满足后续材料烧蚀试验的研究，模型半锥角为10°，前缘半径为0.025 m，其几何模型如图4 所示. 来流马赫数为8，来流环境取20 km高空环境，静温217 K，静压 5475 Pa，来流组元 N2、O2质量分数分别为77%及23%，碳/碳复合材料的性能如表1所示.

采用二维模型进行计算，利用Ansys ICEM对流场模型进行网格划分，网格为四边形结构化网格，流场壁面边界层中的网格质量直接影响到气动热环境的数值模拟和热流计算，对模型壁面附近网格进行加密，以满足壁面边界层对网格的要求，外部流场模型的网格数量为5251. 材料模型采用Abaqus中的四边形CPE4T热力耦合单元，网格数量为2355. 流场与碳/碳前缘模型网格分布如图5所示. 初始时刻材料前缘模型温度为300 K，耦合计算时间步长为 ∆t= 0.01，耦合计算总时长为 30 s，以此来分析材料模型温度分布、壁面烧蚀速率以及烧蚀外形的变化.

3 计算结果及分析

图4 碳/碳复合材料前缘模型Fig.4 Leading edge of carbon/carbon composite

表1 碳/碳材料性能参数Table 1 Performance parameters of carbon/carbon materials

通过计算，可以得到不同时刻外部流场以及材料模型响应的结果. 在t= 20 s时，外部流场马赫数及温度的云图分布如图6所示，在模型头部前端形成激波，在驻点区附近，马赫数较小，接近于0，驻点处流场温度最高可达到2860 K.

图7为材料前缘模型烧蚀20 s后与初始状态对比的位置云图，材料表面产生了明显的烧蚀后退，由图可以看出在驻点区发生了较为严重的烧蚀，在侧面部分烧蚀量较小，该现象从图8烧蚀深度沿壁面的分布情况也可看出. 产生这种现象的主要原因是由于是驻点区材料模型表面温度较高，化学反应更为活跃，进而导致烧蚀氧化速度更快.

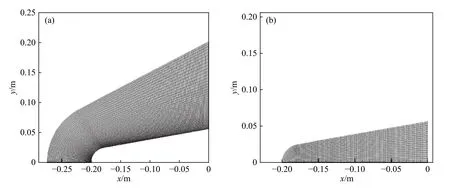
图5 外部流场及材料模型网格划分. （a）流场网格示意图；（b）材料前缘模型网格示意Fig.5 External flow field grids and material model:(a) external flow field grids; (b) leading edge model grids

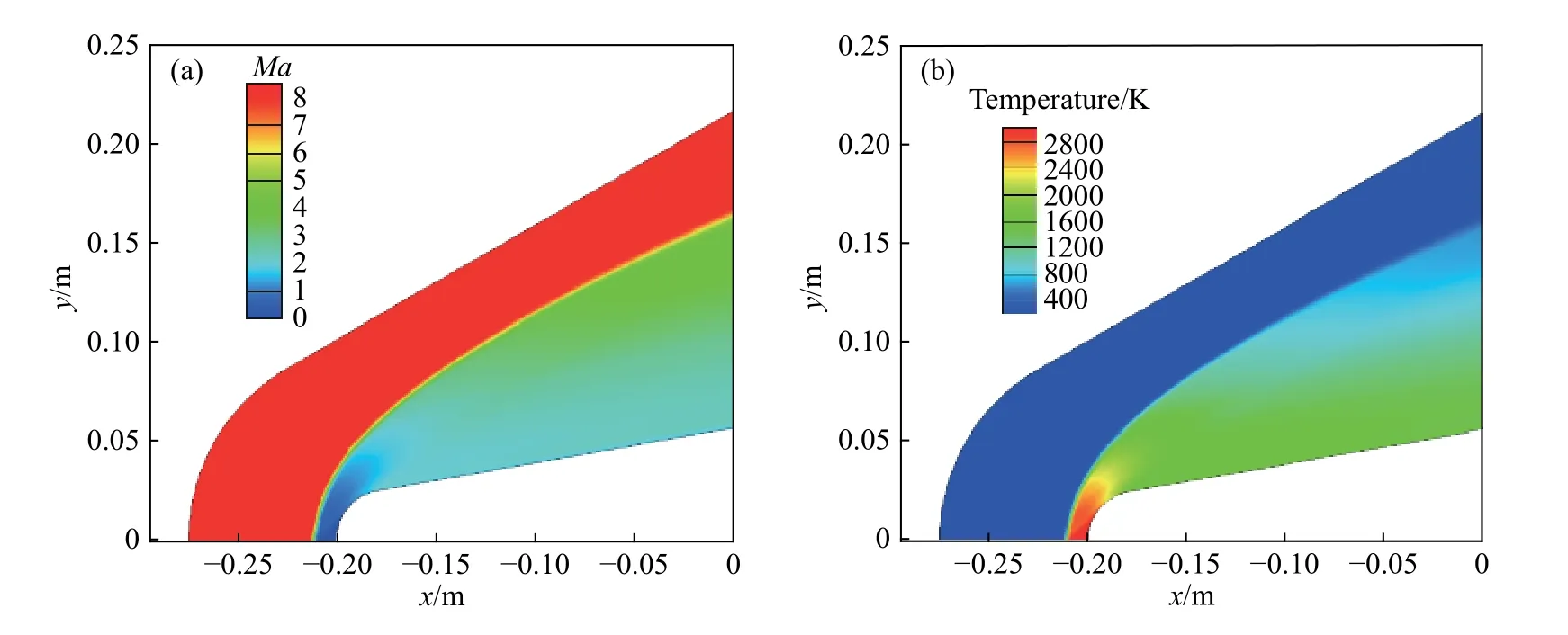
图6 流场马赫数（a）和温度（b）云图分布Fig.6 Mach (a) and temperature (b) distribution of the flow field

图7 材料模型的烧蚀外形Fig.7 Material model ablation profile

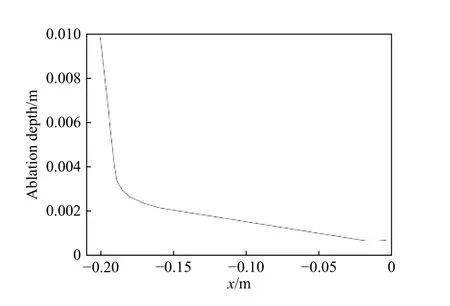
图8 材料模型壁面烧蚀深度分布Fig.8 Distribution of the ablation depth along the wall

通过计算可得到不同时刻热流密度的分布情况，如图9所示，驻点区热流密度最大，远离驻点区热流密度随之减小，随着烧蚀时间的推进，驻点区热流密度减小. 这是由于热流密度的大小与壁面附近温度梯度的大小有关，温度梯度越大，热流值也越大. 在初始时刻，外部流场与材料模型发生热交换，流场温度较高，由于热传导存在一定的延迟性，材料壁面温度较低，此时壁面附近的温度梯度较大，导致热流密度也较大，随着热量不断向材料模型内部进行传递，材料模型的温度场也随之逐渐升高，使得温度梯度变小，热流密度也就变小. 同时也说明了如果采用非耦合模型，将无法预测到热流密度的变化，从而高估热载荷的大小.图10为材料模型壁面温度分布情况，由图可以看出随着烧蚀时间的推进，驻点区壁面温度升高较快，而远离驻点区的壁面温度升高较慢，同时也验证了壁面热流变化的原因.

图9 不同时刻壁面热流分布Fig.9 Heat flow distribution

图10 不同时刻外壁面的温度分布Fig.10 Distribution of wall temperature

图11为预测不同时刻材料模型的烧蚀外形，随着烧蚀时间的推移，模型烧蚀后退深度逐渐增大，10、20、30 s时刻材料驻点所对应的烧蚀深度分别为 3.42、9.86、17.47 mm，材料模型头部半径也逐渐变大，耦合模型考虑了外形变化对气动热环境的影响. 图12为驻点处烧蚀速率随着时间的变化情况，驻点处在开始阶段烧蚀速率变化最大，而在之后变化逐渐缓慢，10、20、30 s时刻材料驻点所对应的烧蚀速率分别为 0.548、0.725、0.795 mm·s−1，这是由于开始阶段的高热流导致材料表面温度迅速升高，进而导致烧蚀速率也迅速变大，随着烧蚀时间的推移，材料表面温度上升，温度梯度减小，导致热流密度减小，进而表面温度趋于平稳，材料的烧蚀速率也将逐渐趋于平稳.

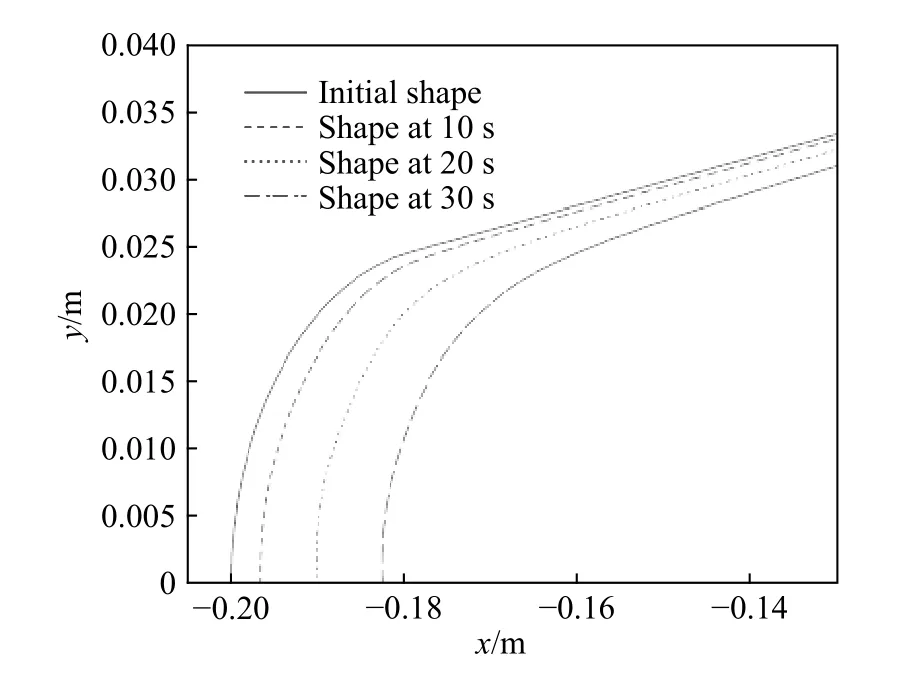
图11 烧蚀外形预测Fig.11 Ablation profile prediction

图12 驻点处烧蚀速率随时间的变化Fig.12 Rate of recession at the point of stagnation

通过以上分析可以看出，在高超声速气动热环境下碳/碳复合材料前缘模型的头部区域将产生一定的烧蚀后退，从而导致外部流场发生变化，使得气动热载荷发生变化. 已有的相关模型未考虑流固双向耦合，忽略烧蚀后退对气动热载荷的影响，将导致气动热载荷预测产生较大的误差，从而影响碳/碳复合材料模型烧蚀响应的有效预测.

4 结论

（1）考虑热化学非平衡效应、固体材料传热以及材料表面热化学烧蚀，建立了高超声速流场与碳/碳复合材料烧蚀响应的双向流−热−烧蚀多场耦合模型，并对碳/碳复合材料前缘模型的传热及烧蚀响应进行了预测.

（2）碳/碳复合材料前缘模型初始阶段驻点区热流值最大，随着烧蚀时间的推移，材料壁面温度逐渐升高，驻点区温度梯度变小，热流值也减小.壁面温度和热流随时间都发生了显著的变化，因此采用多场耦合模型可更好的预测流场及材料响应的变化过程.

（3）在高超声速气动热服役环境下，碳/碳复合材料前缘模型驻点区的温度较高，材料表面反应活跃，烧蚀最为严重，而模型侧面只发生少量烧蚀，烧蚀前后材料模型外形产生一定的变化，前缘半径增大.