非奇异M-矩阵Hadamard积的最小特征值的下界估计

李 华，穆静静，李永献，兰奇逊

(河南城建学院 数理学院,河南 平顶山 467036)

Cn×n(Rn×n)表示n阶复(实)矩阵集, 记Zn为所有非对角元素都为非正数的方阵的集合。设A=(aij)∈Zn如果A=αI-P,其中P>0,α≥ρ(P)则称矩阵A为M-矩阵.如果α>ρ(P)称矩阵A为非奇异M-矩阵. 非奇异M-矩阵的集合记为Mn·称τ(A)=min{|λ|:λ∈σ(A)}为矩阵 的最小特征值, 其中σ(A)为矩阵A的谱集合.

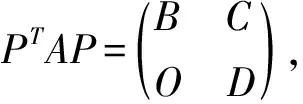
设A∈Mn且不可约, 则存在正向量v使得vA=τ(A)v,称向量v为A的左Perron特征向量.

先引入以下记号：设A=(aij)∈Rn×n,aii≠0,∀i,j,k∈N,j≠i,t=1,2,…,

设A=(aij),B=(bji)∈Cn×n，称矩阵C=A。B=(cij)=aijbij为矩阵A与B的Hadamard积.

由文献[1]知, 如果A和B都是M-矩阵, 则B。A-1也是M-矩阵. 若A∈Mn则存在一个正对角矩阵D,使得D-1AD是行严格对角占优的M-矩阵.

设A=(aij),B=(bij)∈Mn,A-1=(aij),对于τ(B。A-1)的估计，有如下结果：

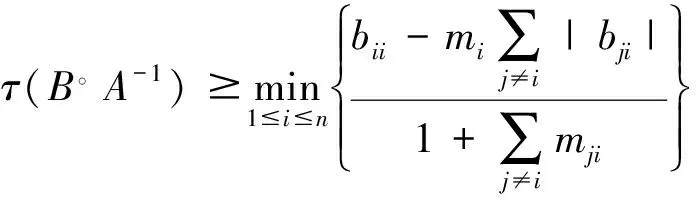
2017年赵建兴等[5]得到：

本文继续对非奇异M-矩阵B和非奇异M-矩阵A的逆矩阵A-1的Hadamard积的最小特征值进行估计，得到τ(B。A-1)的单调递增收敛的下界序列，且新的估计式改进了文献[3-5]的相应结果.

1 非奇异M-矩阵研究的主要结果

引理1[1]设A,B∈Rn×n,D,E为两个正对角矩阵, 则有

D(A。B)E=(DAE)。B=(DA)。(BE)=(AE)。(DB)=A。(DBE)

引理2[6]设A=(aij)∈Cn×n,xi>0,i=1,…n,则矩阵A的所有特征值位于下列区域的并集中:

引理 3[2]设A=(aij)∈Cn×n,xi>0,i=1,…n,则矩阵A的所有特征值位于下列区域的并集中:

引理 4[5]设A=(aij)是行严格对角占优的矩阵, 则∀i,j∈N,j≠i,t=1,2,…,有

定理1 设矩阵A=(aij),B=(bij)∈Mn,A-1=(αij),则对任意的t=1,2,…,有

证明：当n=1时, 显然成立，假设n≥2.

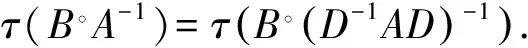
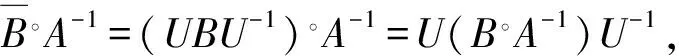
则有：

若A和B中至少有一个是可约矩阵,设D=(dij)为置换矩阵, 其中d12=d23=…dn-1,n=dn1=1,其余的dij=0,则对任何正实数t,A-tD,B-tD的所有顺序主子式是正的,从而A-tD,B-tD为非奇异不可约M-矩阵,用A-tD,B-tD分别代替A,B, 让t→0由于连续性, 则可得到上述同样的结果.

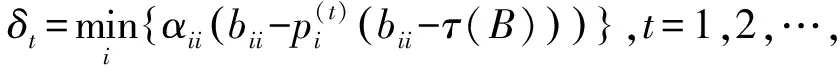
定理2 序列{δt}是单调递增且有上界的序列，因此是收敛的.

定理3 设矩阵A=(aij),B=(bij)∈Mn,A-1=(αij),则对任意的t=1,2,…,有

证明：当n=1时, 显然成立.假设n≥2.

由于A∈Mn,则存在正对角矩阵D,使得D-1AD为行严格对角占优的 矩阵.由于D-1(B。A-1)D=B。D-1A-1D=B。(D-1AD)-1,即τ(B。A-1)=τ(B。(D-1AD-1)).不失一般性,可设A为行严格对角占优的M-矩阵.

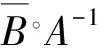
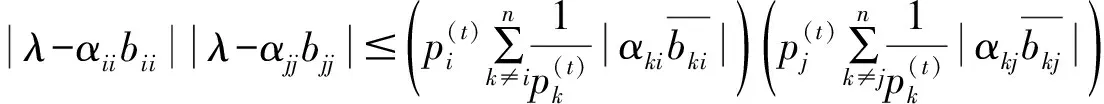
若A和B中至少有一个是可约矩阵,设D=(dij)为置换矩阵, 其中d12=d23=…=dn-1,n=dn1=1,其余的dij=0则对任何正实数t,A-tD,B-tD的所有顺序主子式是正的, 从而A-tD,B-tD为非奇异不可约M矩阵, 用A-tD,B-tD分别代替A,B,让t→0由连续性, 则可得到上述同样的结果.

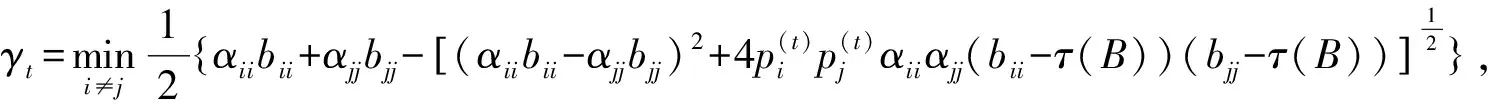
定理4 序列{γt}是单调递增且有上界的序列，因此是收敛的.

定理5 设矩阵A=(aij),B=(bij)∈Mn,A-1=(αij),则有

证明: 不失一般性, 当i≠j时, 假设

定理6. 设矩阵A=(aij)∈Mn,A-1=(αij),则有

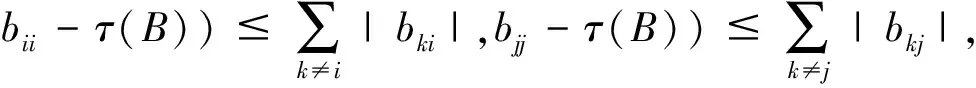
即定理5的结果优于文献[5]中定理1的结果.

注2：由文献[5]的定理3和定理4知，当A=(aij),B=(bij)∈Mn有：

当A-1是双随机矩阵时，有：

即定理5的结果要优于文献[3]～[5]的相应结果.

2 数值算例分析

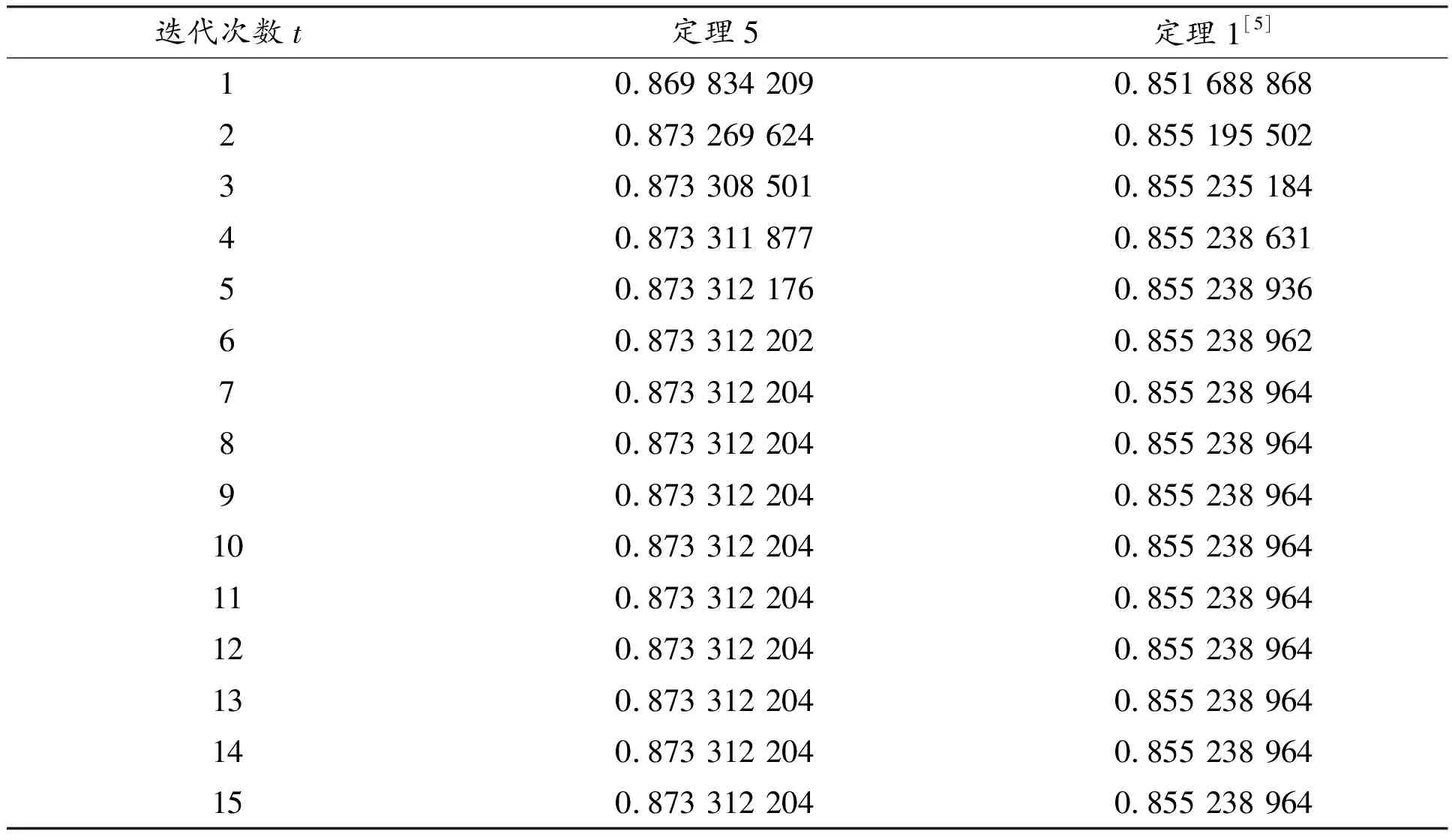
表1 τ(A。A-1)的下界估计

事实上，τ(A。A-1)=1。从表1可以看出：

(1)从定理5得到的τ(A。A-1)的下界序列是单调递增且有极限的序列;

(2)由定理5得到的τ(A。A-1)的下界优于文献[5]中相关结果得到的下界;

(3)在当前精度下，当迭代次数为12的时候，下界序列有极限值.

3 结论

本文给出了非奇异M-矩阵B和非奇异M-矩阵A的逆矩阵A-1的Hadamard积的最小特征值τ(B。A-1)下界的估计式，估计式是单调递增收敛的下界序列，数值算例表明新的估计式在一定条件下改进了已有结果.