重庆铁路转体桥不平衡重称重与配重试验研究

赵 琳，李梦微，刘晓亮，梁 斌

(1.中铁十五局集团第三工程公司，四川 成都 610097；2.河南科技大学 土木工程学院,河南 洛阳 471023)

随着我国交通基础设施建设快速发展，跨线桥梁越来越多，转体施工法应运而生。通过在既有线路两侧施工再利用转体设备将其旋转对接合拢，能够避免施工期间干扰既有线路交通运行，转体桥适用范围越来越广泛。转体时需满足易转、稳定[1]两大条件，即转体结构处于一定平衡状态。施工中存在误差及外界干扰，转动体重心偏离转动中心轴线导致悬臂两端出现重量差，由于某些部位尺寸与设计尺寸相比存在一定偏差，悬臂两端重量差无法按设计尺寸进行理论计算，需要根据称重试验进行配重，否则拆除固结及其他约束时可能会由于偏载过大而引起梁体发生偏转，对安全不利。因此，需要进行不平衡重称重试验及配重，测试转体梁的不平衡力矩、偏心距等参数，给出转体桥配重平衡条件，为转体方案制定及实施提供决策依据[2]。研究转体桥不平衡重称重试验与施工控制技术，对当前国内外桥梁技术发展有重要价值。

目前，国内外学者主要采用理论与试验数值分析相结合的方法研究此类问题。文献[3]以吉林四平市东丰路上跨铁路斜拉转体桥工程为依托，设定并核查转体牵引系统一系列参数并对其进行施工，对转体结构进行顺桥向和横桥向称重试验及配重研究以确保桥梁顺利转体，通过试转及精确定位保障桥梁转体就位，形成转体施工关键技术方案；文献[4]结合某T构转体桥工程，根据结构在偏压状态的受力规律，推算出基于球铰应力差法下的不平衡力矩理论公式，结合有限元模型分析球铰结构，对不平衡力矩数值进行预估，并与称重试验实测数据对比，表明两种方法下不平衡力矩计算结果相差不大，应力差法估算不平衡力矩是合理的，可根据其结果配重，节约耗材、简便精确；文献[5]以武汉长丰大道高架桥工程为背景，对称重原理以及球铰摩阻系数进行理论分析，称重试验后按照小偏心脱空转体方案配重，并计算系统牵引力，为桥梁顺利转体精准到位提供了保障；文献[6]结合新建张唐铁路跨大秦铁路大桥工程，进行转体前的称重试验，对绝对平衡配重及不同偏心距的倾斜配重方案进行抗倾覆能力评估，建立上部结构和球铰结构的有限元模型，对其进行抗风应力验算，结合两种配重方案的优劣分析以及安全系数评估，采用倾斜配重方案，桥梁转体过程安全平稳；文献[7]以石家庄某铁路上跨桥工程为依托，对关键工况下梁体的应力及线形进行模拟分析及实时监控，转体前对其进行称重配重研究，提出T构平衡配重方案，确保其顺利转体。目前对于转体桥不平衡重的研究已取得诸多成果[8-11]，但对西南地区上跨既有铁路桥梁的不平衡重研究相对较少。

以重庆市位于YDK0+603.19～YDK3+168.59标段铁路枢纽东环线珞璜南右线特大桥工程为依托，通过进行不平衡重称重及配重试验研究，分析测试转体梁不平衡力矩、摩阻力矩、偏心距、摩阻系数，得到转体桥梁配重方案，在此基础上，形成转体桥不平衡重施工控制技术，进而指导工程施工。

1 工程概况

重庆珞璜南右线特大桥位于重庆市江津区境内，全长2 565.4 m，是重庆铁路枢纽东环线上最长桥梁，作为重庆市第一座上跨既有铁路转体桥，也是施工的重难点工程，转体施工前梁边距既有线回流线水平距离为4.6 m，且工程地质复杂。该桥采用(44+80+44)m单箱单室变截面连续梁跨越既有渝贵线铁路并与其呈23.11°，如图1所示，梁顶宽7.6 m，底宽4.5 m。为避免施工干扰既有线路交通运行，在铁路两侧各自进行悬臂施工从而形成平行于既有线路的T构梁体，再进行转体，转体就位后依次对边跨、中跨段进行合拢施工。转体桥墩采用实心墩，转体主墩承台分为两个台阶，在上下承台之间设置转体系统。转体系统由球铰、撑脚、滑道、牵引设备等组成，上、下球铰球面半径为11 m，箱梁底部设置有8个撑脚，在转体过程中球铰作为主要受力点，撑脚与滑道接触，两支点共同参与受力，避免T构出现晃动甚至倾覆，保证梁体平稳转体，转体角度23.11°，转体总重量5 400 t。

图1 重庆铁路转体桥效果图

2 称重与配重试验

2.1 试验目的

桥梁转体前，需要对其进行称重试验，以保证转体施工顺利进行。桥梁施工中存在诸多因素可能导致桥梁两端出现重量不平衡问题，如梁段齿块差异、附属结构差异、设计误差、施工误差，还有温度变化引起的测量误差，这些因素将会引起桥梁重心偏离转动中心轴线，最终导致不平衡力矩的产生，由于存在外界因素的影响，无法通过理论计算来平衡。桥梁转体前，必须通过称重试验得到不平衡力矩、偏心距等参数，并按要求对其进行配重，为桥梁转体提供数据支撑及安全保障。

2.2 称重试验原理

2.2.1 转动体不平衡力矩计算与球铰摩阻力矩

本试验中，采用球铰转动法来测试不平衡力矩，这种测试方法的前提是需要假设梁体围绕球铰发生了刚体转动，通过对T构一侧施加顶力从而对梁体产生转动力矩，位移发生突变时即为球铰发生刚体转动的瞬间。拆除梁体的临时支架，完成砂箱的施工后，梁体的平衡状态有以下两种形式：

(1)转动体球铰摩阻力矩大于转动体不平衡力矩

设转动体重心偏向北侧，若不平衡力矩计算结果为负值，重心则偏向南侧。依次向南北侧施加P1、P2进行顶升，直到球铰发生微小转动。顶南侧梁时，见图2，得到平衡方程式(1)：

P1L1+MG=MZ

(1)

顶北侧梁时，见图3，得到平衡方程式(2)：

P2L2=MG+MZ

(2)

式中，L1为P1距球铰中心距离(m)，L2为P2距球铰中心距离(m)，MG为不平衡力矩(kN·m)，MZ为摩阻力矩(kN·m)。

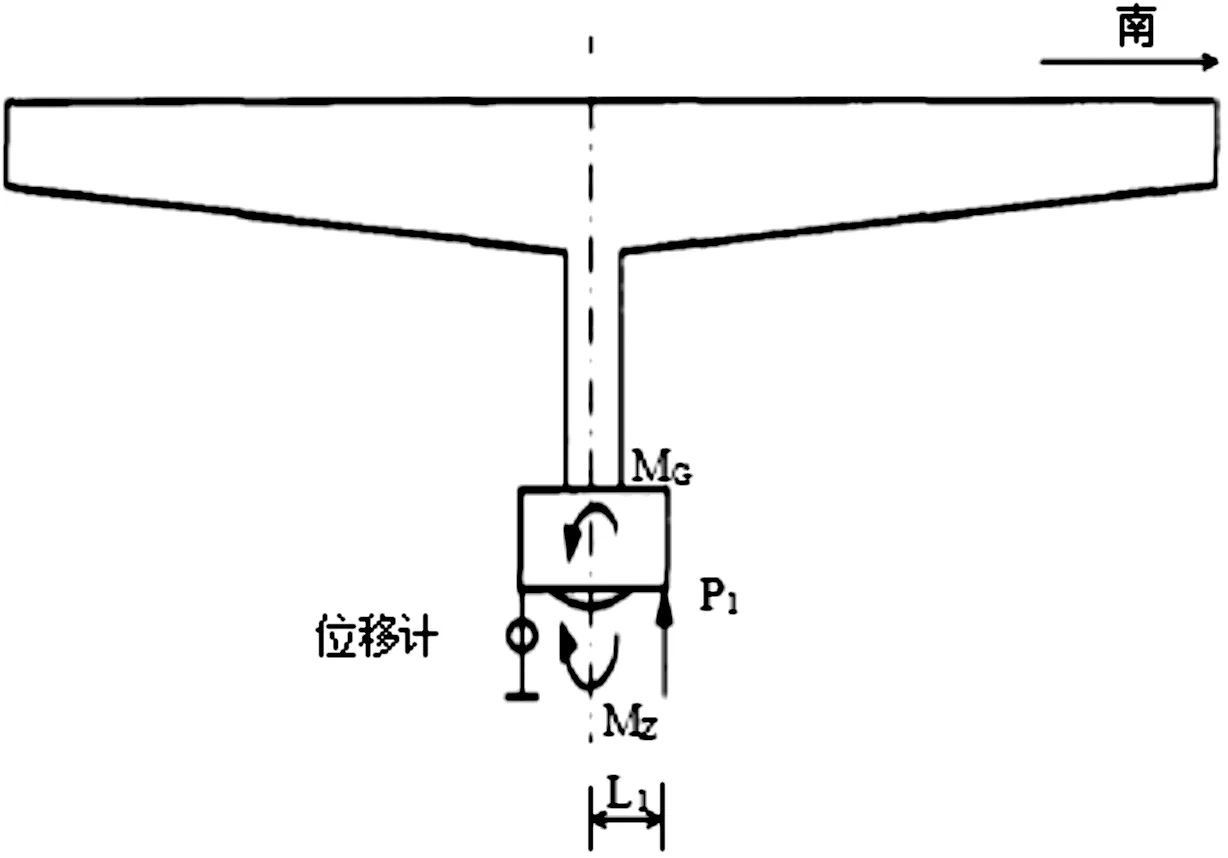
图2 MZ与MG反向

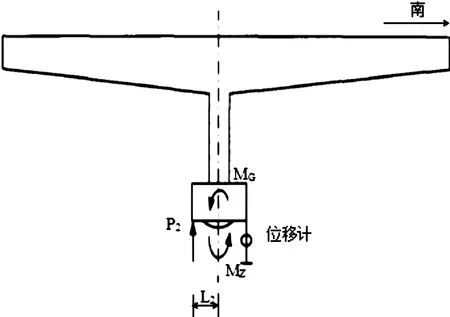
图3 MZ与MG同向

解方程式(1)和(2)，不平衡力矩MG按照公式(3)进行计算：

(3)

摩阻力矩MZ按照公式(4)进行计算：

(4)

(2)转动体球铰摩阻力矩小于转动体不平衡力矩

设转动体重心偏北侧，此种情况下，只能在北侧依次进行升顶、落顶，见图3。当P2升至临界力的瞬间，得到平衡方程式(5)：

P2L2=MG+MZ

(5)

千斤顶回落至P3，球铰发生微小转动，得到平衡方程式(6)：

P3L2=MG-MZ

(6)

解方程式(5)和(6)，不平衡力矩MG按照公式(7)进行计算：

(7)

摩阻力矩Mz按照公式(8)进行计算：

(8)

2.2.2 摩阻系数及偏心距

通过理论公式结合实验数据，球铰摩阻系数μ按照公式(9)进行计算：

(9)

转动体偏心距e按照公式(10)进行计算：

(10)

式中，R为球铰球面半径(m)，G为转体重量(kN)。

根据以上原理及公式，结合本工程实例进行参数计算，通过试验得到球铰运动瞬间即刚体位移发生突变时的顶力值，计算主要参数，包括不平衡力矩、摩阻力矩、摩阻系数和偏心距，根据该数据制定配重方案。

2.3 理论配重

由于T构两端预应力锚固齿块差异、部分T构位于线路平面曲线上、施工误差和其他荷载等因素影响，称重试验前应进行合理理论配重，避免解除临时固结和拆卸砂箱时转动体结构由于两端不平衡力矩过大发生偏转，出现安全隐患。29、30号墩是桥梁的转体墩，选取30号墩进行理论配重，结果表明，30号墩纵、横桥向不平衡力矩分别为3 017.6 kN·m(向中跨方向偏心)、252.7 kN·m(向曲线内侧偏心)，由于横向偏心较小，不进行配重，称重试验前在边跨侧距梁端4 m位置放置 7 t试块作为配重。

2.4 称重设备及测点布置

(1)量程50 mm位移传感器4个，精度0.01 mm，见图4。

(2)量程400 kN压力传感器4台，最大精度1 kN。

(3)智能综合测试仪4台用于压力采集。

(4)400 t千斤顶4台，见图5。

(5)笔记本电脑、数码相机各1台。

所有设备布置如图6所示。

图4 位移传感器

图5 千斤顶

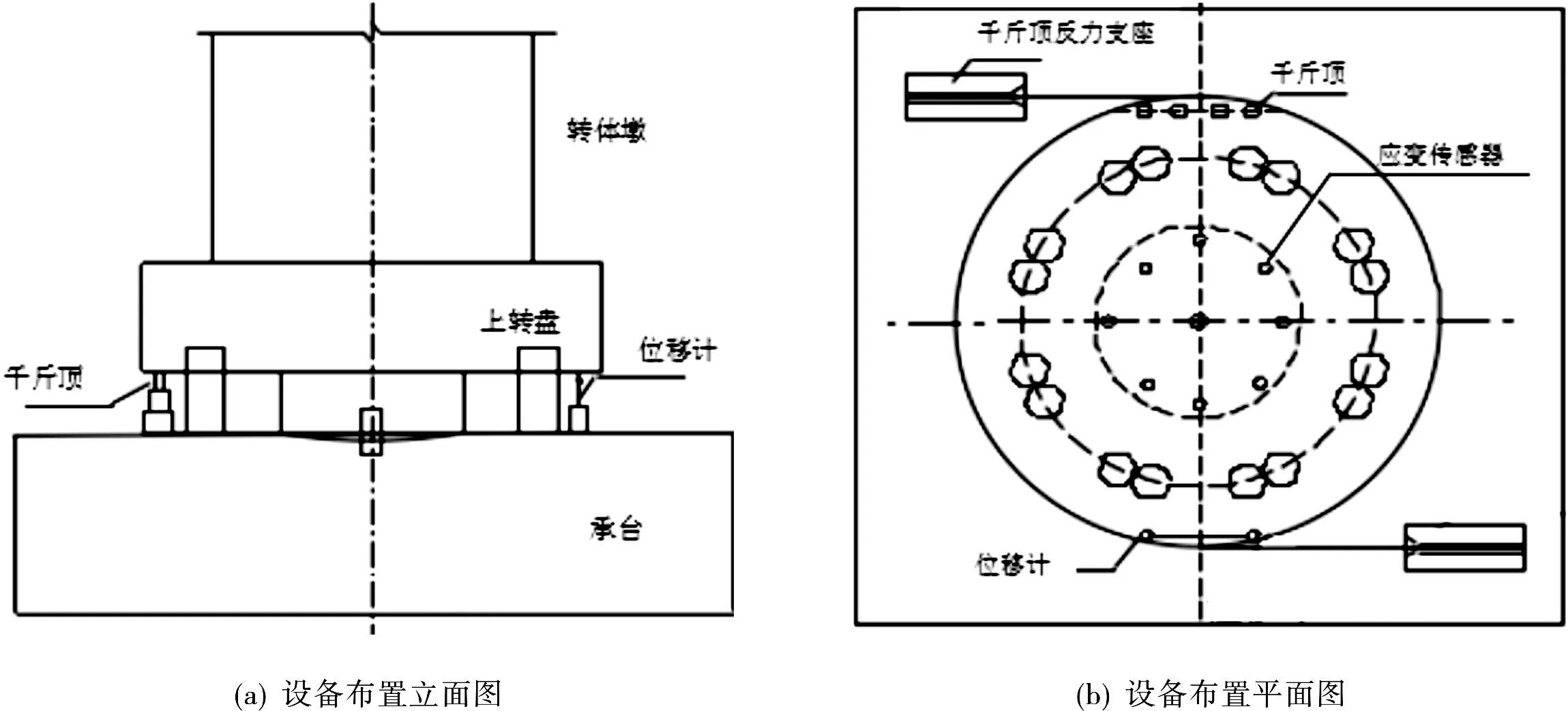
图6 设备布置图

2.5 试验步骤

图7 称重试验过程图

(1)拆除临时结点，观察撑脚的情况，进而判断T构平衡状态。

(2)在位移测点处安装位移传感器，另一侧上转盘底部放置千斤顶，见图7。调整位移传感器及压力传感器至预压状态，逐级加压，记录压力值和位移读数，仔细观察位移值，直到位移值产生突变，记录压力值。

(3)按照实际工程所处平衡状态，进行降顶或对调仪器位置升顶，记录压力值和位移读数，绘制P-S曲线图。

(4)重复(2)至(3)步一次，形成两次试验数据，防止由于转体系统老化或测量误差导致数据偏差过大。两次结果相差不大，说明该试验结果可靠。

(5)计算主要参数，包括不平衡力矩、摩阻力矩、摩阻系数和偏心距，制定配重方案。

3 试验结果分析

3.1 试验结果

由于篇幅原因，论文以30号墩纵向及横向称重为例。解除临时固结后，T构撑脚与滑道未接触，可判定为第一种平衡状态，顶力与位移测试数据见表1，根据表1绘制纵向称重顶力与位移关系图见图8。

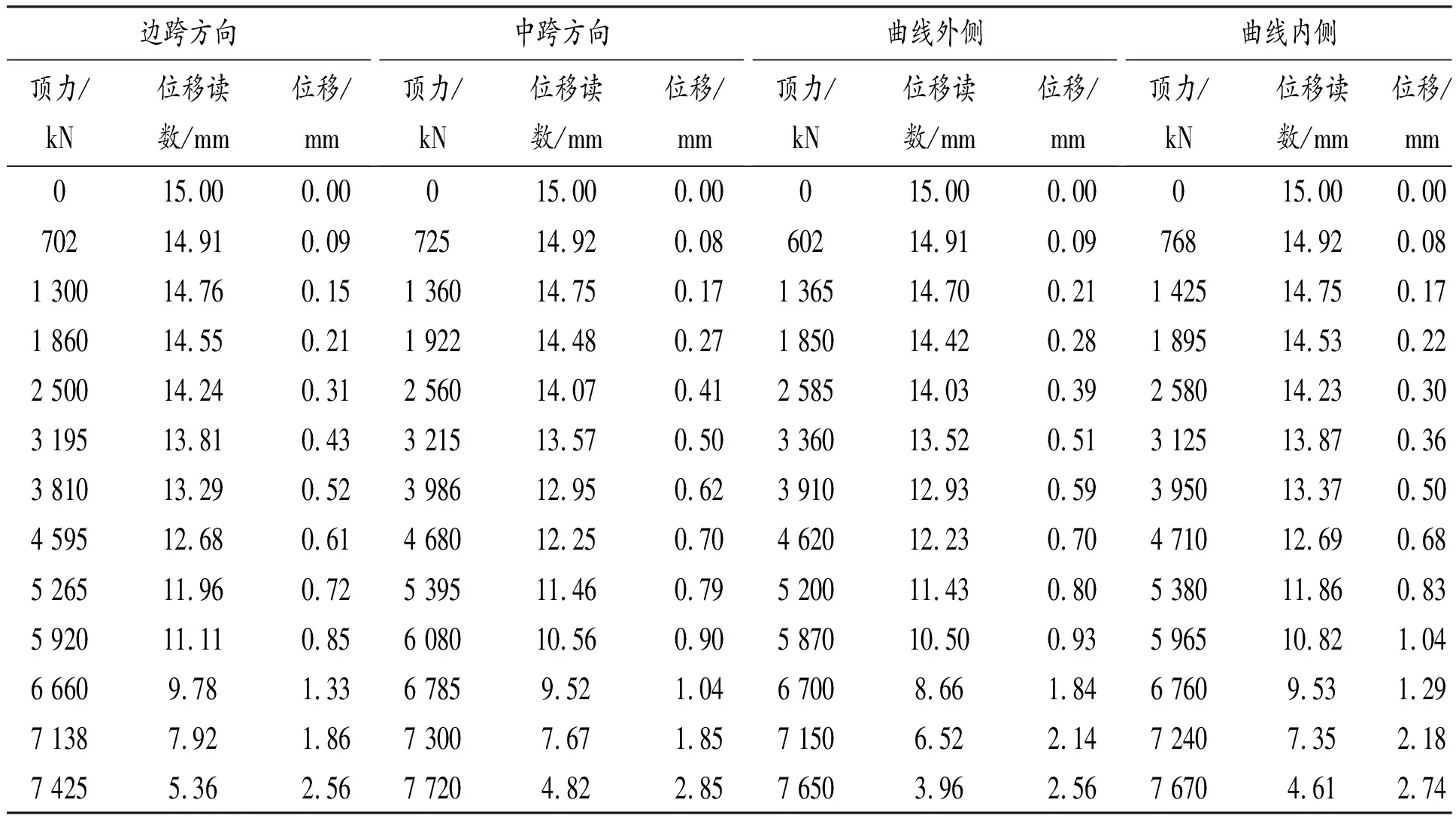
表1 30号墩称重试验数据

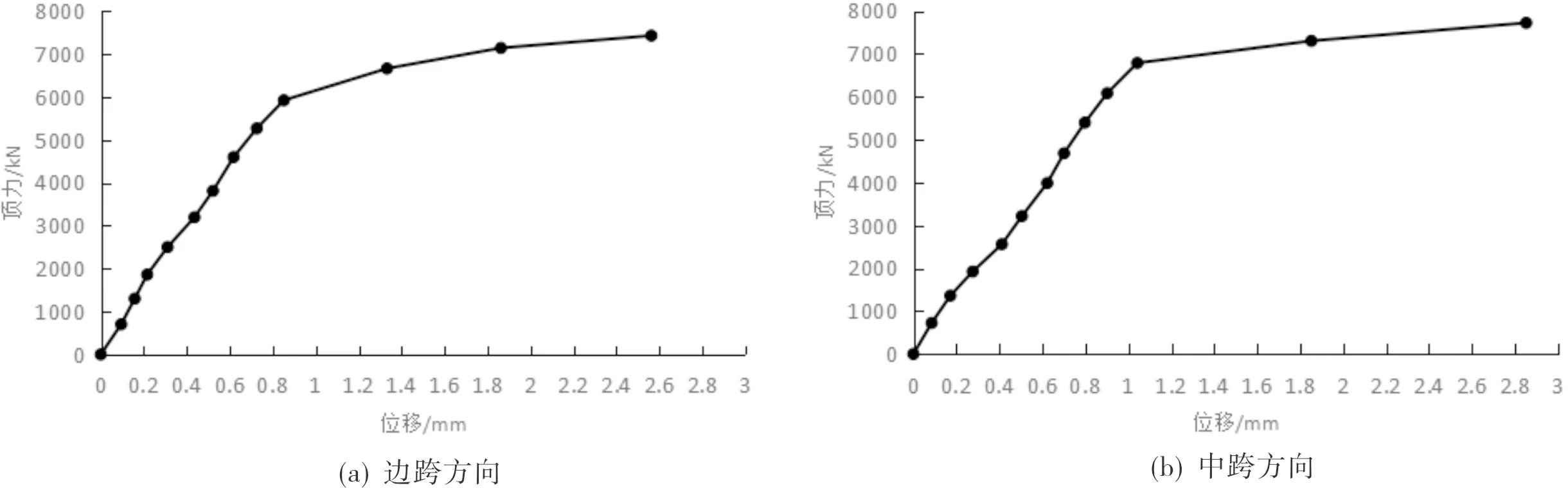
图8 30号墩顶力与位移图(纵向)

由表1可知：30号墩纵向及横向称重时，位移随顶力的增大而逐渐增大，在加载初期，位移缓慢增大，T构处于静摩擦状态，未发生转动，边跨方向当顶力由5 920 kN加载至6 660 kN时，位移由0.85 mm突然增至1.33 mm，中跨方向当顶力由6 785 kN加载至7 300 kN时，位移由1.04 mm突然增至1.85 mm，曲线外侧当顶力由5 870 kN加载至6 700 kN时，位移由0.93 mm突然增至1.84 mm，曲线内侧当顶力由6 760 kN加载至7 240 kN时，位移由1.29 mm突然增至2.18 mm，转动体由静摩擦状态转化为动摩擦状态，球铰发生微小转动。

由图8可知：假设重心偏向中跨侧，边跨侧顶升临界力P1=6 660 kN，中跨侧顶升临界力P2=7 300 kN，L1=3.96 m，L2=4.01 m，R=11 m，G=5 400 t。代入公式(3)、(4)、(9)、(10)，解得不平衡力矩MG=1 449.7 kN·m，摩阻力矩MZ=27 823.3 kN·m，摩阻系数μ=0.048，偏心距e=0.027 m。因此，重心偏向中跨侧。

同理，假设重心偏向曲线内侧，曲线外侧顶升临界力P1=6 700 kN，曲线内侧顶升临界力P2=7 240 kN，L1=4.02 m，L2=3.99 m，R=11 m，G=5 400 t。代入公式(3)、(4)、(9)、(10)，解得不平衡力矩MG=976.8 kN·m，摩阻力矩MZ=27 910.8 kN·m，摩阻系数μ=0.048，偏心距e=0.018 m。因此，重心偏向曲线内侧。

3.2 配重

常采用的配重方案包括：绝对平衡方案，纵向倾斜方案。第一种方案是通过增加T构一侧质量使得重心与转动中心轴线重合，仅由球铰支撑转体进行受力，转体全过程撑脚与滑道无接触，可近似看为单支点受力，所需牵引系统的牵引力小，由于外界干扰及牵引惯性可能会引起T构转动不平稳，在竖向平面发生摇摆；第二种方案是通过增加T构一侧质量使得重心偏离转动中心轴线，保证偏心距在5～15 cm，转体过程中撑脚与滑道接触，两支点共同参与受力，所需牵引系统的牵引力较大，保障转动平稳进行。实际施工一般采用第二种方案，配重时考虑实际空间问题，在非跨铁路一侧设置配重，保障施工可行性及安全性。

本工程30号墩的T构纵向、横向偏心距分别设置为0.05 m、0 m，纵向配重在边跨设置，重量为10.4 t，距离球铰中心40 m，横向配重在曲线外侧设置，重量为27.9 t，距球铰中心3.5 m。

3.3 牵引力计算

通过计算牵引力，保证T构顺利精准转体就位，由于采用倾斜配重方案，转体过程撑脚与滑道接触，需要考虑撑脚作用力的影响，避免牵引力设置过小转动体无法启动或转体无法精准就位。因此，牵引力F按照公式(11)进行计算：

(11)

转体重量G=54 000 kN，球铰平面半径r=1.75 m，转台直径D=8.5 m，撑脚支反力N=2 000 kN，撑脚所在位置的回转半径R=3.45 m，启动时静摩擦系数μ=0.1，转动时动摩擦系数μ=0.06，将以上参数代入公式(1)中，启动时所需最大牵引力822.4 kN，转动过程中所需牵引力493.4 kN。

3.4 效果评价

图9 竣工图

本工程在转体前进行不平衡称重试验研究取得了极大成效，保证桥梁顺利平稳转体到位，为大桥转体阶段提供了施工参数及安全保障。2018年11月26日至27日，完成T构称重及配重，12月18日凌晨，在两台千斤顶牵引下，位于既有渝贵高铁两侧的5 400 t T构桥梁历时30 min逆时针转体23.11°，顺利精准转体就位，合拢最大偏差为6 mm，轴线精度在2 mm以内。山城重庆第一次实现转体桥梁对既有铁路成功跨越，证明配重方案的可行性。转体桥施工竣工图见图9。

4 结论

(1)采用球铰转动法对重庆跨铁路转体桥在转体前进行称重试验研究，根据顶力与位移曲线图，找出临界力，并结合理论分析计算梁体的不平衡力矩、偏心距、摩阻力矩、摩阻系数，根据纵向倾斜配重法得到转体桥配重方案以确保转体平稳进行，为转体方案的制定及实施提供决策依据。

(2)横向及纵向称重试验中，在加载初期，30号墩位移随加载缓慢增大，位移突然增大时，转动体由静摩擦状态转化为动摩擦状态，球铰发生微小转动，对应顶力即为所求临界力。

(3)经过不平衡称重测试分析得转体桥30号墩纵向不平衡力矩1 449.7 kN·m，偏心距0.027 m，横向不平衡力矩976.8 kN·m，偏心距0.018 m。配重时30号墩T构纵向、横向偏心距分别设置为0.05 m、0 m，纵向配重在边跨设置，重量为10.4 t，距离球铰中心40 m，横向配重在曲线外侧设置，重量为27.9 t，距球铰中心3.5 m。启动、转动时所需牵引力分别为822.4 kN、493.4 kN。

(4)通过对转体桥进行称重试验及配重研究，制定合理可行的配重方案，解决由于外界因素导致T构出现不平衡力矩，转体角度23.11°，历时30 min转体到位，转体过程平稳顺利，证明称重试验及配重方案的合理性，可为同类型施工提供参考。