非线性西原体模型及其应用

卢小雨,王 游

(1.安徽理工大学 力学与光电物理学院,安徽 淮南 232001；2.安徽理工大学 土木建筑学院,安徽 淮南 232001)

岩体巷道与支护工程的长期稳定性和安全性与岩石在长期应力状态下的力学行为密切相关，这种与时间有关的力学行为称之为岩石的蠕变[1]。建立合适的岩石蠕变模型是研究岩石蠕变的方法之一，线性元件由于参数少，物理意义明确且能描述岩石蠕变复杂的力学特性而被广泛应用于蠕变模型中，但基于线性组合元件构建的蠕变模型对加速蠕变阶段的描述并不十分理想。建立起能全面描述岩石蠕变各个阶段和蠕变机理的模型是目前岩石蠕变学研究的热点和难点[2-5]。针对这一课题，众多研究学者主要采用以下两种方法：(1)用新的非定参数元件代替蠕变模型中的线性元件，例如，宋勇军[6]对灰质板岩进行分级加载下的蠕变研究，采用FC元件组合建立一种非线性Burgers模型，该模型在不同加载应力水平下都能较好地描述岩石三个蠕变阶段，何志磊[7]通过把西原体模型中的牛顿体用软体元件替代，从而建立了基于分数阶的蠕变模型，并对模型参数进行敏感性分析；(2)依据岩石蠕变硬化和软化机理，采用损伤力学和断裂力学等新理论建立起岩石非线性蠕变模型，例如，罗润林[8]通过引入损伤变量和黏性系数硬化函数，建立起能全面反映软岩黏弹塑性蠕变机制和损伤特征的蠕变模型，宋勇军[9]基于岩石蠕变过程中的蠕变硬化效应和软化损伤机理，建立起能全面描述岩石蠕变特性曲线的非线性蠕变模型，赵延林[10]基于Kachanov损伤理论，将Burgers模型和非线性M-C塑性元件串联组合，形成的BNMC蠕变损伤模型合理地模拟了岩石的黏弹塑性和蠕变损伤，王瑞红[11]基于初始压力与卸载压力之差建立了损伤变量表达式，并引入Burgers模型建立非线性蠕变模型，该模型可以较好地描述岩石蠕变全过程，吴飞[12]通过假定损伤变量为时间的负指数形式并考虑岩石加载应力的影响建立一个非线性蠕变模型，并通过蠕变实验验证了其合理性。

文章在前人研究基础上，通过把西原体模型中黏性系数进行非线性化和增加一个考虑岩石弹性模型时效损伤的弹性体，从而建立起能全面描述岩石非线性蠕变特性的蠕变模型，引入相关蠕变实验数据验证模型的合理性与可行性，并对模型参数进行敏感性分析，旨在为相关研究提供参考。

1 非线性蠕变模型建立

1.1 修正的Kelvin模型

由于把蠕变参数当成一个定常数，因而传统Kelvin模型无法定性描述岩石蠕变过程中的非线性特征[13-14]。陈文玲[15]认为岩石衰减蠕变阶段其黏性系数随加载时间不断增大，因此假定在Kelvin模型中黏性系数与时间的函数表达式符合式(1)：

η(t)=ηe-λt

(1)

其中：λ为岩石蠕变参数，η为初始黏性系数。

式(1)对时间求一阶导数，可得：

(2)

当λ<0时，η(t)随着加载时间的增加呈非线性增加。

在Kelvin模型引入非线性黏性系数表达式，得到非线性Kelvin模型，如图1所示。

图1 修正的Kelvin模型

修正的Kelvin模型本构方程为：

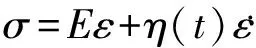
(3)

其中：σ为加载应力，E为Kelvin体弹性模量，ε为蠕变应变。边界条件t=0，ε=0,积分得到该模型的蠕变方程为：

(4)

1.2 加速蠕变阶段岩石损伤模型

关于岩石蠕变损伤问题，目前主要有两种观点[16,17]：一种认为岩石受到应力作用就会产生损伤；另一种认为只有当岩石加载应力超过某一强度时，岩石才进入损伤阶段并产生随加载时间逐渐积累的损伤。本文基于第二种观点，即只有当加载应力超过岩石长期强度时才有损伤产生且损伤随加载时间的增加而增加直至岩石破坏。但事实上岩石加载应力超过岩石长期强度时，岩石往往要经过一定时间的加载才产生较为明显的损伤，故在线性元件中引入损伤变量时，一般也要引入岩石加速蠕变起始时间[5]。按照损伤力学理论，本文损伤变量采用岩石弹性模量变化来定义，即当岩石蠕变处于加速阶段时，损伤变量演化方程可描述为[18-21]：

(5)

其中：E0为岩石初始弹性模量,E∞为岩石长期弹性模量，λ为与岩石损伤程度相关的系数，tF为岩石加速蠕变起始时间。

假定岩石材料为各向同性体损伤，则E(t)可简化为：

(6)

当t=0，D=0，对应于岩石无损伤；当t=∞，D=1，对应于岩石完全损伤且加速蠕变阶段岩石损伤变量非线性增大。对于无损伤岩石来说，其弹性应变εe与加载应力σ的关系符合胡克定律：

(7)

当岩石加载应力超过岩石长期强度时，根据Lemaitre等效应力原理[22]，将式(6)代入式(7)可得：

(8)

式(8)为岩石加载应力超过岩石长期强度时，考虑岩石弹性模量时效损伤的弹性体蠕变方程。

1.3 非线性蠕变模型

传统西原体模型能够较好地描述岩石蠕变曲线从而被广泛应用到岩石蠕变模型中，但在许多情况下西原体模型对岩石衰减蠕变的描述并不十分理想，一是因为用来描述岩石衰减蠕变的Kelvin 模型的黏性系数是一个定常数；二是因为西原体模型难以描述岩石进入加速阶段的蠕变变形。因此，为了建立起能全面描述岩石三个蠕变阶段的模型，用非线性Kelvin模型代替Kelvin模型，再增加一个考虑岩石弹性模量时效损伤的弹性元件来描述岩石的加速蠕变，修正后的模型如图2所示。

图2 修正的黏弹塑性模型

根据元件组合特性，列出方程组如式(9)所示：

(9)

一维蠕变方程为：

(10)

(11)

1.4 三维蠕变方程

(12)

处于弹性体状态下的岩石内部任一点的应力σij可由球应力张量σiiδij和偏应力张量Sij组成，仿照应力组成形式，应变εij也可分解为球应变张量σiiδij和偏应变张量eij。由弹性理论可知，弹性本构关系的三维张量表达形式为：

(13)

其中：σii为体积应力，εii为体积应变，Sij为应力偏量，eij为应变偏量，K为弹性体体积模量，G0为弹性体剪切模量。

(14)

其中：G1为开尔文体的剪切模量。

对于黏塑性体的三维蠕变方程为：

(15)

损伤弹性体的三维蠕变方程为：

(16)

其中：G2为损伤弹性体剪切模量。

对于常用的屈服函数一般采用Mises函数，若塑性流动法则采用相关联流动准则时，即F=Q，在常规三轴压缩蠕变实验中，应力满足第一不变量和偏应力第二不变量，把应力不变量带入式(13)～式(16)中，可得非线性蠕变模型的三维轴向蠕变方程：

(17)

(18)

其中：σ1为第一主应力，σ3为第三主应力，其余参数和式(13)～式(16)中参数意义一致。

2 模型辨识及参数敏感性分析

2.1 参数辨识及模型验证

基于蠕变实验数据，选用合适的数据拟合方法对模型参数进行反演辨识是蠕变研究中不可或缺的部分。已有相关学者给出模型参数的辨识方法，在此不再详述，利用Origin软件自带的Levenberg-Marquardt算法进行非线性回归分析，得到岩石蠕变模型参数。

利用白垩系冻结软岩蠕变试验数据[23]验证文中建立的非线性蠕变模型合理性和适用性，对蠕变实验数据进行数据拟合，模型曲线与实验数据对比见图3，参数反演结果见表1。

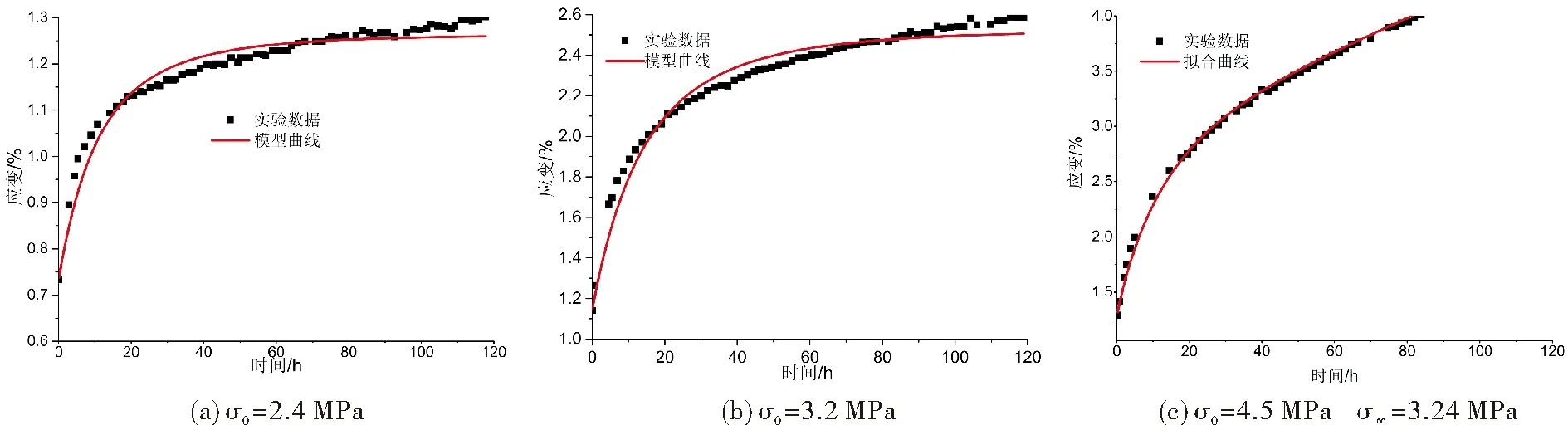
图3 软岩非线性蠕变模型与实验数据对比

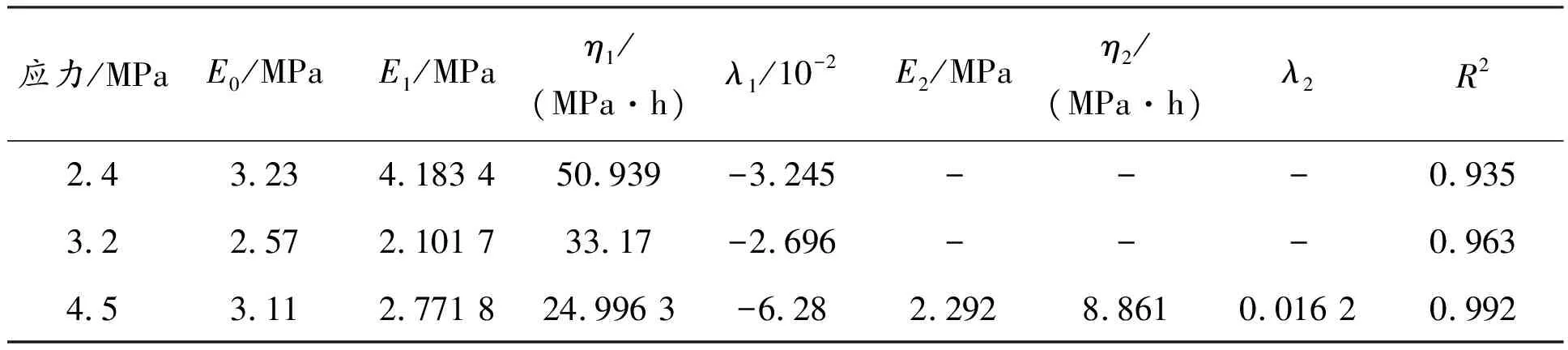
表1 软岩非线性蠕变模型参数

由图3(a)、(b)可知：文中建立的非线性蠕变模型在岩石衰减蠕变阶段拟合结果与实验数据吻合良好，证明了文中建立的修正Kelvin模型的适用性和合理性；由图3(c)可知，建立的非线性蠕变模型与岩石加速蠕变阶段拟合结果良好，这表明基于岩石弹性模量时效损伤建立的岩石加速蠕变模型是合理的。

利用页岩蠕变实验数据[24]再次验证建立的非线性蠕变模型合理性和适用性，模型曲线与实验数据对比如图4所示，参数反演结果见表2。

图4 页岩非线性蠕变模型与实验结果对比

表2 页岩非线性蠕变模型参数

由图4可见，建立的非线性蠕变模型与页岩蠕变实测曲线吻合的相当好。

2.2 参数λ2敏感性分析

由于岩石加速蠕变特性是影响地下结构和工程岩体稳定性和安全性的重要力学参数之一，故进一步给出了模型参数λ2的敏感性分析，如图5所示。

图5 参数λ2的敏感性分析

图5给出了参数λ2对蠕变模型曲线的影响规律，其他参数模型取值见表2加载应力为55 MPa时的数值。从图5可以看出：随着参数λ2取值的增大，岩石蠕变应变量和蠕变速率也相应增大，岩石损伤随加载时间的增加而急剧增加，岩石表现为迅速破坏，更快地进入加速蠕变阶段，表明建立的蠕变模型对不同加载应力和不同岩性的岩石加速蠕变曲线都具有较好的适用性。

3 结论

(1)在西原体模型基础上将黏性系数非线性化，并增加一个损伤弹性体，实现了线性元件非线性表达，得到了一个能够描述岩石蠕变硬化和岩石加速蠕变损伤的非线性模型，该模型解决了传统线性组合模型无法定性和定量描述岩石衰减蠕变和岩石加速蠕变损伤机理的问题，且模型中参数具有明确的物理意义，并基于元件特性给出了一维蠕变方程和三维蠕变方程。

(2)引入白垩系冻结软岩蠕变实验数据和页岩蠕变实验数据进行蠕变曲线拟合，结果表明建立的非线性西原蠕变模型与实验数据吻合程度良好(尤其是加速蠕变阶段)，初步表明了建立的蠕变模型可以较好地描述岩石各个阶段蠕变的非线性，该模型能够揭示岩石衰减蠕变机理和损伤破坏机制。

(3)通过对岩石蠕变参数λ2进行敏感性分析，表明随着参数λ2的增大，岩石进入加速蠕变的时间越短，岩石蠕变破坏更加剧烈。