基于模板滑窗处理测量数据中野值的方法*
李红军,吕绍杰,张永华,叶旭鸣
(1 国防科技大学计算机学院, 长沙 410073; 2 天津津航计算技术研究所, 天津 300308)
0 引言
大量的研究数据表明,无论是基于最小二乘理论的模型参数估计、各种经典滤波方法及其改进的方法(如KF、EKF、UKF等),还是频谱分析中的极大熵谱估计技术,对采样数据中包含的野值反应都极为敏感[1]。而由经验和统计理论可知,即使是高精度的测量设备,在受到多种偶然因素的影响后也往往包含有较大的随机误差,一般偏离目标真值1%~5%,严重时甚至达10%~20%的误差[2]。测量数据中出现的这些野值对数据的处理存在很大影响,如在目标跟踪中,野值会导致滤波发散,目标丢失[3]。因此,针对测量数据中连续出现多个野值,依据测量数据的前后相关性和变化规律,提出了一种基于模板滑窗滤除测量数据中野值的方法,消除野值对测量数据处理工作的影响。
1 算法描述
测量数据中野值出现的形式如图1,孤立型、斑点型野值示意图如图2。文中的算法流程如图3所示,首先设置滑动模板窗口大小及系数值,窗口的大小依据所处理的数据需要来设置,滑动模板的系数依据最小二乘原理获得;随后滑动模板窗口,卷积计算预估值;再把预估值与实际测量值进行比较,如满足误差限要求,则判断为真实值,计数器增加,模板滑动一位,否则判为野值点,进入下一步;下一步判断前两个测量点是否为野值点,如不是,则预估值直接替代测量的野值点,且计数器增加,如是,则转入连续野值点判别。
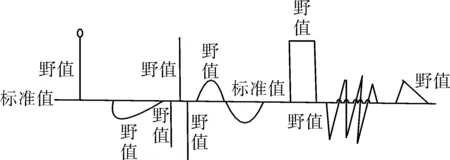
图1 测量数据中野值出现的不同形式示意图
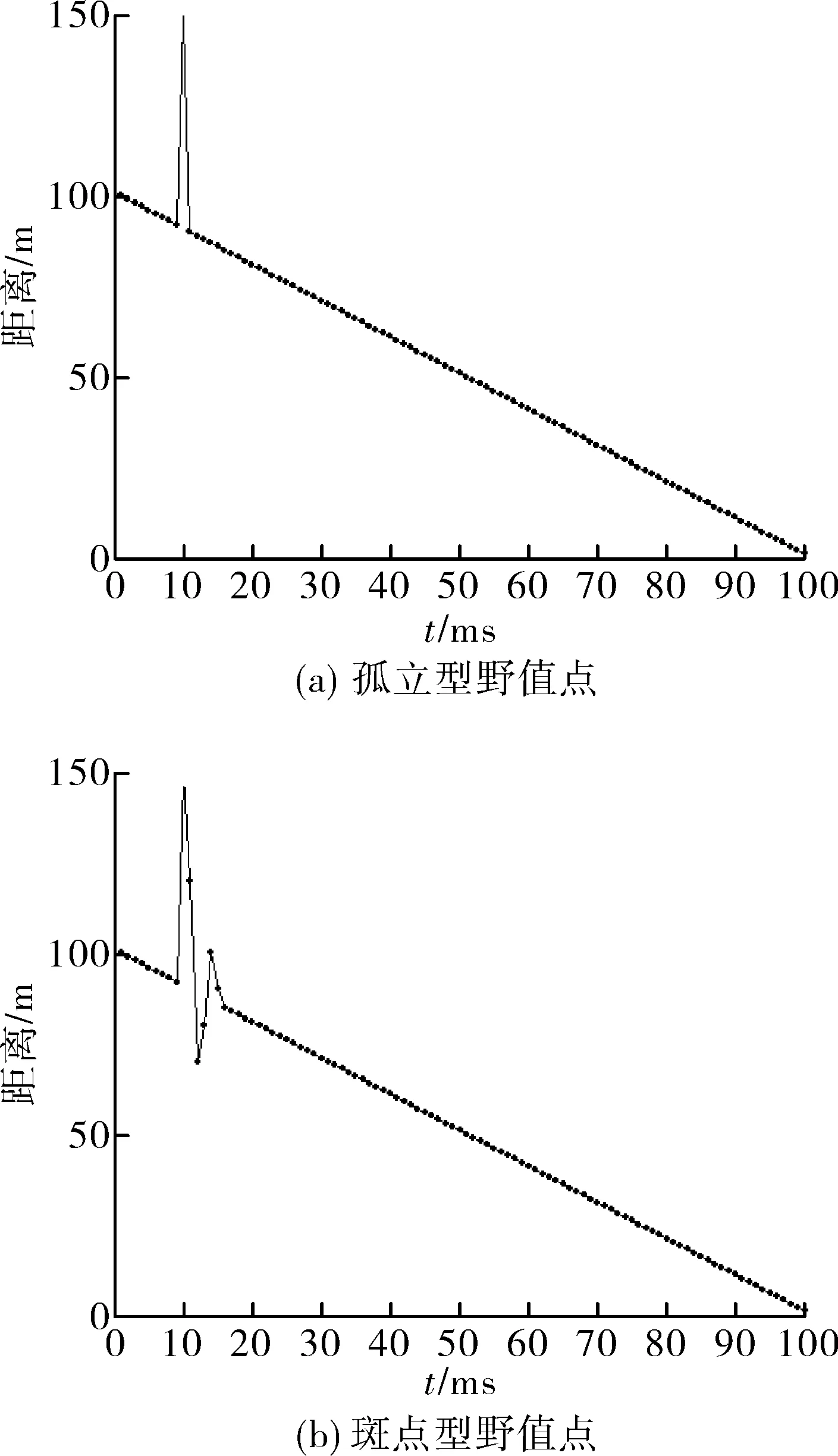
图2 不同类型野值示意图

图3 算法流程图
1.1 设置滑动模板窗口长度和系数值
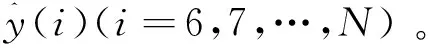
(1)
式中:
(2)
设置滑动模板的系数值如下:
aj=c1+c2j,j=1,2,…,n
(3)
则滑动模板窗口长度为5的系数a1=-0.2,a2=0,a3=0.2,a4=0.4,a5=0.6,如图4所示。

图4 滑动模板窗口长度和对应的系数值
1.2 滑动模板与对应测量数据卷积
将滑动模板最右端对准要进行野值判别点的前一个数据,滑动模板上的各个系数与滑动模板下各对应测量数据相乘,并将所有乘积相加,得到滑动模板卷积的结果,即预测值。

(4)
重复上述步骤,使得滑动模板在测量数据中遍历,直至处理完所有的测量数据。
1.3 设置阈值并比较预测值与测量值

1.4 基于测量数据变化规律进行连续测量点判别
从式(3)和图4可知,滑动模板的系数之和为1,模板第1个系数与第3个系数的大小相等,符号相反;第2个系数为零;第4个系数与第5个系数之和为1。也就是说估计值中权重最大的是第5个系数对应的值,其次是第4个系数对应的值,这也说明了相邻两个数据之间的相关性最大,数据相距越远相关性越小。因此,当野值连续出现小于3个时,不进行判断,当野值连续出现大于2个时,进行判断,第3个估计值则根据连续实测值的变化趋势估测该时刻位置的测量值,当判断连续3个为预测值时,取第1个预测值前面连续5个点,求取其平均值,将第3个预测值减去计算出的平均值,从而得到新的预测值。滑动模板窗口按照采样时间在测量数据中逐位移动,遍历全部测量数据,直至测量数据采样结束。
2 实验结果及分析
文中进行了仿真实验和试验测量数据验证算法的有效性,其中采用的滑动模板窗口长度为5,对应的系数为a1=-0.2,a2=0,a3=0.2,a4=0.4,a5=0.6。试验数据如图5所示,仿真数据如图6所示,其中仿真数据人工模拟加入了孤立型野值点、连续型野斑点,连续型野斑点包括振荡型野斑点,大小幅值递增或递减型野斑点,幅值相等型野斑点。处理结果如图5~图12所示。

图5 试验数据和野值剔除结果

图6 仿真数据和野值剔除结果

图7 仿真数据中孤立型野值点处放大图

图8 仿真数据中小幅值递增或递减型野斑点处放大图

图9 试验数据中孤立型野值点处放大图

图10 仿真数据中振荡型野斑点处放大的图

图11 仿真数据中幅值相等型野值点处放大图

图12 仿真数据中大幅值递增或递减型野斑点处放大图
图5是试验数据野值剔除结果,其中尖锐突出为孤立型野值点,粗直线为剔除野值后的数据。图6 是仿真数据野值剔除结果,其中粗直线表示的是处理后的结果。图7、图8、图10、图11、图12是仿真数据野值剔除结果放大图,图9是试验数据野值剔除结果放大图。可以看出,算法自适应性强,能够处理不同类型的野值点,证明该算法有效。
3 结论
针对测量数据中存在连续出现多个野值,依据测量数据的前后相关性和变化规律,提出了一种基于模板滑窗滤除测量数据中野值的方法,消除了连续多个野值对测量数据处理工作的影响,避免了连续野值造成误估计情况的发生。试验结果表明,该算法自适应性增强,能够处理不同类型的野值点,而且简单有效,可以实际应用。

