基于FEKO软件的高分辨距离像建模仿真*

李昱琛，索继东

(大连海事大学信息科学技术学院， 辽宁大连 116026)

0 引言

高分辨率一维距离像(HRRP) 是用宽带雷达信号获取的目标散射点子回波在雷达射线上投影的向量和。雷达带宽的提高使得电大尺寸目标的检测和识别成为可能，高分辨距离像能够反映出船舰等电大尺寸目标上的细节特征并且其图像更加容易获取，因此基于HRRP的雷达目标识别成为国内外研究热点[1]。

HRRP的获取主要可以分为实际测量法和理论仿真法。实际测量法包括外场实测法和紧凑场测量法[2]。理论仿真法主要为利用专业的电磁仿真软件仿真得到目标的距离像。由于实际测量法对设备要求高且实验过程比较复杂，而理论仿真法相对简单且易于实现，因此常用理论仿真法获取目标的一维距离像[3-4]。

文献[5]仿真了某个姿态角下船舰目标的高分辨距离像，仿真结果与实际模型一致，验证了仿真方法的有效性和准确性。文献[6]仿真获取目标全极化回波数据，进而对获取的数据进行处理，通过IFFT变换生成一维距离像，实现了全极化HRRP的生成。文献[7]介绍了一种基于OpenGL技术的高分辨距离像仿真方法，通过比较说明了仿真结果的有效性。文献[8]采用点散射中心模型对三类舰船进行了建模仿真，并将得到的距离像用于目标识别。上述文献都验证了FEKO仿真高分辨距离像的可行性。然而，实际目标一定会处在特定的环境中，环境因素极易影响目标回波，上述仿真方法虽然都从各自目标本身特征出发，研究了高分辨距离像的获取方法，但对目标环境因素对目标的影响尚无具体的研究。因此，文中在上述文献的基础上研究了海面环境对船舰目标RCS的影响，最后仿真了在海面背景下的高分辨距离像的影响，综合说明了在海面环境影响下理论仿真法仍然具有可行性。

1 FEKO建模及其算法研究

利用FEKO进行仿真一般分为以下步骤，首先建立目标三维模型，然后对建立的三维模型进行网格划分和遮挡面的判别，对模型施加宽带信号得到三维目标的RCS，最后利用IFFT得到目标的高分辨距离像。其流程图如图1所示。

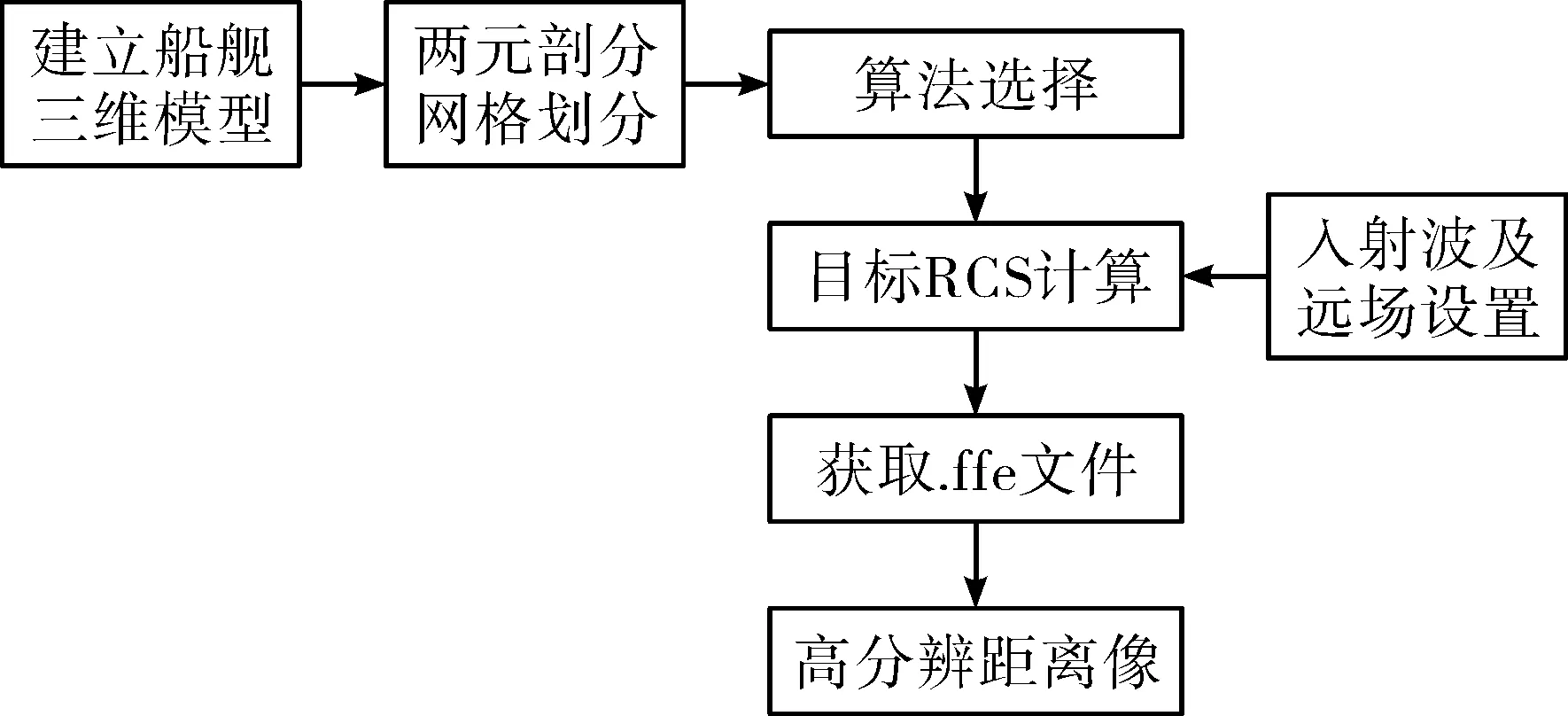
图1 高分辨距离像仿真流程图

1.1 FEKO船舰模型的建模

FEKO提供了多种建模的方式，可以利用自带的建模模块建立三维模型，也可以从专业的三维仿真软件(例如ACIS、IGES、Unigraphics等)中导入模型。文中所选模型为利用FEKO建立的某船舰目标三维模型。

1.2 二维粗糙海面模型的建立

采用二维随机粗糙面模拟海面模型，在联合北海波浪工程(JONSWAP)海洋波谱模型的基础上，设置模型参数。JONSWAP海洋波谱模型可以表示为[9]：

(1)

根据浅水重力毛细作用扩散关系，海浪频率f和k的关系如下：

(2)

式中：d是海水深度；k是海浪的波数；km=363.2 rad/m为具有最小相位速度的波数。

因此海面波谱可以表示为：

SF(f)=S(f)η(d)

(3)

其中

(4)

1.3 FEKO的主要算法

FEKO的核心算法是矩量法(MOM)，除此之外还包括有限元法(FEM)、多层快速多极子方法(MLFMM)、物理光学法(PO)等。

MLFMM就是对附近区的强耦合量进行直接计算，而对非附近区的弱耦合量采用多层快速多极子方法进行计算。MLFMM采用树形结构，其特点是逐层聚合、逐层转移、逐层配置[10]。

PO是一种利用散射体表面电流积分表示散射场的方法，常被用作高频电磁近似计算。通过对感应场近似积分得到相应的空间场，用物理光学表面电流密度近似表示物体表面的感应电流。物理光学算法能够快速准确的计算电大尺寸目标的特性，被广泛应用于电大尺寸目标的仿真当中[11]。

对于复杂目标的RCS可以用其多个散射单元回波RCS的总和来近似表示，散射单元的RCS可以通过PO来得到，对于理想导体，其总场的切向分量包括：

n×ET=0

(5)

n×HT=2n×Hi

(6)

式中Hi是表面单元处的入射磁场。当入射波与i同向，磁场方向与hi平行，磁场强度为H0时物理光学积分可表示为：

(7)

根据式(7)可得RCS的平方根物理光学表达式为：

(8)

根据以上原理可以计算目标的RCS。

2 目标RCS及高分辨距离像计算

2.1 目标网格剖分

FEKO自带网格剖分工具，可以将目标模型剖分，也可以采用专业的网格划分软件划分网格，再将划分好的网格导入FEKO中。模型网格剖分的数量和大小对最后仿真的质量和速度会产生很大影响，FEKO默认的三角形面网格边长为入射波波长的1/8。

2.2 目标RCS计算

利用FEKO计算目标RCS可以分为以下几步[12]:1)模型建立。建立简单模型，设置模型参数，也可以导入模型。2)参数设置。设置入射平面波频率和平面波激励方式。3)设置远电场。设计远电场并输出.ffe文件。4)网格划分。通过FEKO软件对模型进行网格剖分，剖分长度为波长的1/8。5)算法设置。选择相应的算法。6)运行仿真。运行FEKO进行仿真。

2.3 目标HRRP的获取

通过FEKO仿真得到回波数据.ffe文件，文件中的数据依次表示theta角、phi角、theta的实部和虚部、phi的实部和虚部，HRRP的具体求法可以是对回波数据文件中的实部加虚部后求傅里叶逆变换(IFFT)，也可以用RCS加其相位后求IFFT。由于回波数据RCS文件中只包含幅度信息，其相位需要由回波数据的实部和虚部通过欧拉变换求出。电场和相位可表示为：

E=(Rθ+Rφ)+i(Iθ+Iφ)

(9)

φ=arctan((Iθ+Iφ)/(Rθ+Rφ))

(10)

式中：Rθ和Rφ分别为theta角和phi角的实部；Iθ和Iφ分别为theta角和phi角的虚部。最后通过Matlab读取.ffe文件，再进行傅里叶逆变换后得到高分辨距离像。

3 目标仿真实验

对某船舰目标简化模型(如图2所示)进行仿真，船舰长70 m、宽8 m，网格划分尺度为1/8波长。

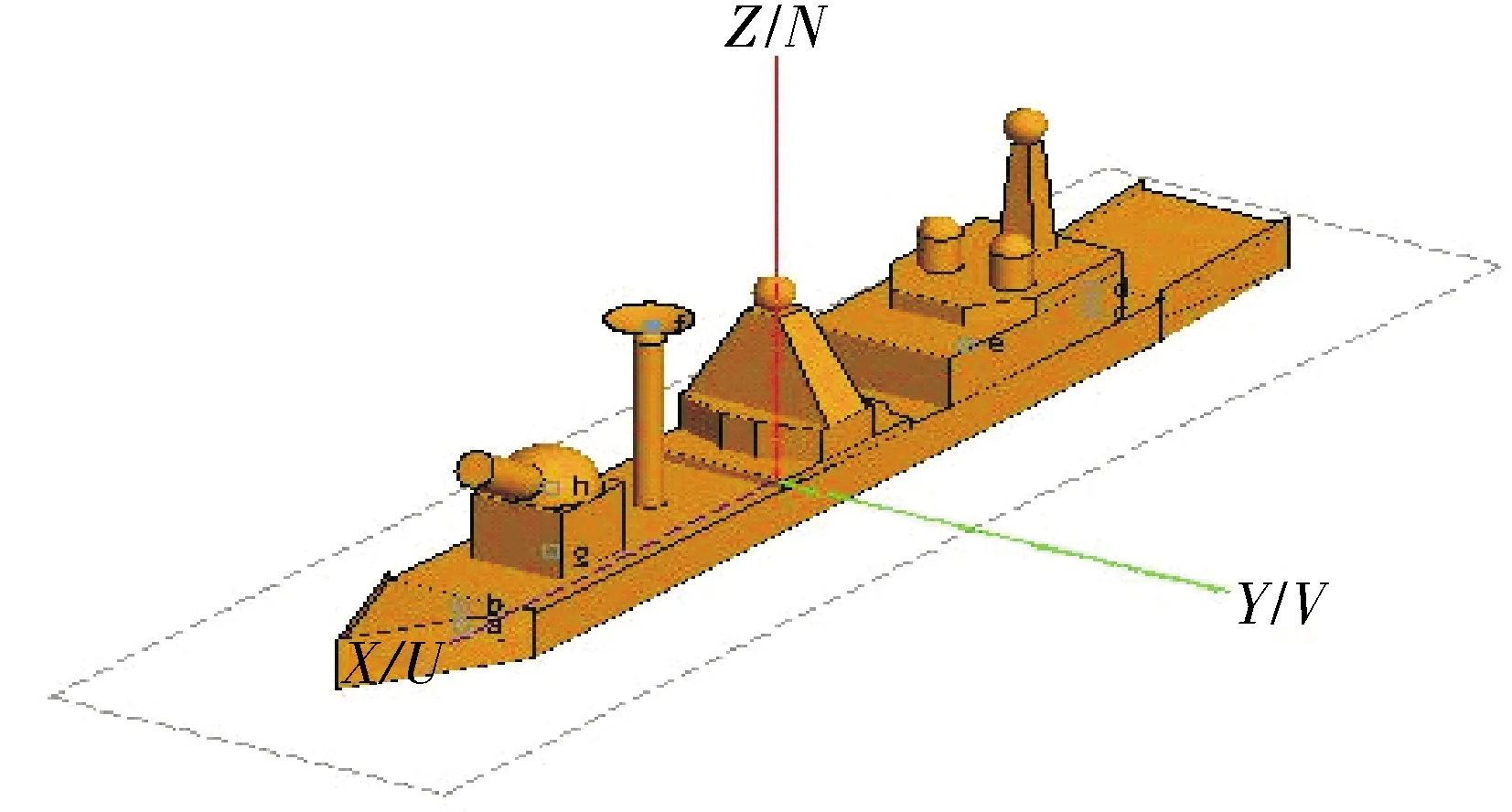
图2 某船舰目标简易模型图

3.1 船舰目标的RCS仿真

通过FEKO软件，使用MOM/PO和MLFMM对船舰目标的回波数据进行仿真分析[12]，并比较两种算法的计算结果和仿真效率。实验的参数设置如下：入射频率为1.6 GHz，俯仰角为90°，方位角范围为0°～180°，极化方式为水平极化。计算了船舰目标0°～180°的单站RCS。计算机CPU配置为主频率3.70 GHz，内存为4 GB。两种算法的计算结果如3图所示。计算过程所划分的网格个数、使用的内存和计算时间如表1所示。

表1 两种仿真方法的对比结果

综合上述仿真结果，通过图3可以看出：两种算法在计算精度上基本相同，但是在0°～30°和150°～180°时有明显差异，这是由于船首船尾处缺少明显的结构，使得两种算法产生计算误差，但是总的误差在可控范围内，因此两种算法仿真结果都具有可行性。从表1可以看出：PO/MOM混合算法可以显著减少仿真的内存和时间消耗。因此在仿真电大尺寸目标时，应优先选取PO/MOM混合算法。

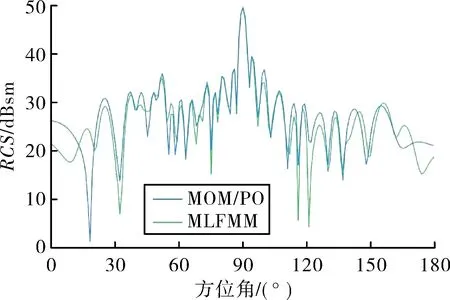
图3 相同条件下高频混合算法与MLFMM算法RCS效果图

3.2 海面环境下目标RCS特性的研究

实际船舰由于处于海面环境中，势必会对其RCS造成影响。海面被模拟为理想电导体(PEC)并且采用JONSWAP海洋波谱模型模拟海面环境[13]。海面上10 m处的风速为3 m/s，风浪区长度为30 km，海水深度为10 m，海水的相对介电常数为εr=55.9，εeff=ε0εr(1-jtanδ)，tanδ=0.67，由上述参数构建海面模型，实验的参数设置如下：入射频率为1 GHz，俯仰角为90°，方位角为-90°～90°，极化方式为水平极化，模拟海面模型下船舰目标的RCS，其与单纯船舰目标RCS仿真结果的比较如图4所示。

图4 海面对船舰目标RCS的影响

从图4可以看出:由于导电平面的存在，目标和海面之间发生相互作用，这使得目标RCS增大。在大入射角照射时，目标RCS增大较小，海面对船舰目标的影响较小；而当小入射角照射时，海面的电磁散射会对目标产生较大影响，使得目标的RCS显著增大，因此在进行高分辨距离像仿真时应充分考虑海面电磁散射的影响。

3.3 姿态角对高分辨距离像的影响

雷达一维距离像同目标与雷达间的姿态角有很大关系，因此一维距离像有姿态敏感性。当目标与雷达直接的相位位置即姿态角发生变化时，目标散射点投影的相对位置会发生改变，使得目标的高分辨距离像发生变化。

选取3个不同的姿态角对船舰模型的高分辨距离像进行仿真，实验所用信号中心频率为12 GHz，频带宽度为200 MHz，方位角为0°代表船首方向照射，方位角为90°代表船舷方向照射，考虑海面电磁散射影响，海面被模拟成一个完美的导电平面。海水的相对介电常数为εr=55.9，电导率为5 s/m，选取方位角为90°，俯仰角为30°，极化方式为水平极化。仿真的目标RCS及高分辨距离像如图5和图6所示。

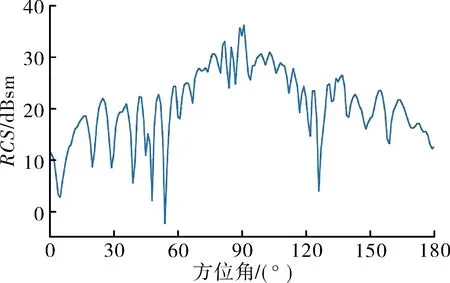
图5 方位角90°、俯仰角30°下的RCS

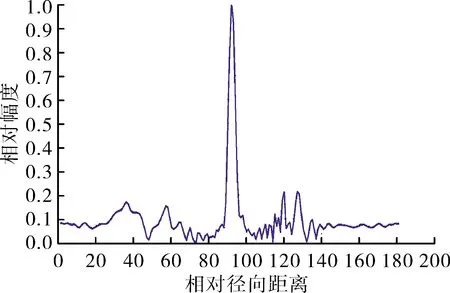
图6 方位角90°、俯仰角30°下的高分辨距离像

选取方位角为0°，俯仰角为30°，仿真结果如图7和图8所示。

通过观察可以看出：不同姿态角下船舰目标的高分辨距离像有很大差异，当从船舷方向照射时(如图7所示)，目标峰值大多集中在相对距离80～100间，而当从船首方向照射时(如图8所示)，目标峰值径向分布较为分散，目标船舷方向相对幅度较大，船首船尾方向相对幅度较小，图中的强散射点分别对应炮台、瞭望台、指挥台等和结构的棱边和尖顶散射而成，仿真结果与模型一致。这说明当海面被模拟为完美导电平面时，通过仿真得到的高分辨距离像在海面背景下具有可行性。

图7 方位角0°、俯仰角30°下的RCS

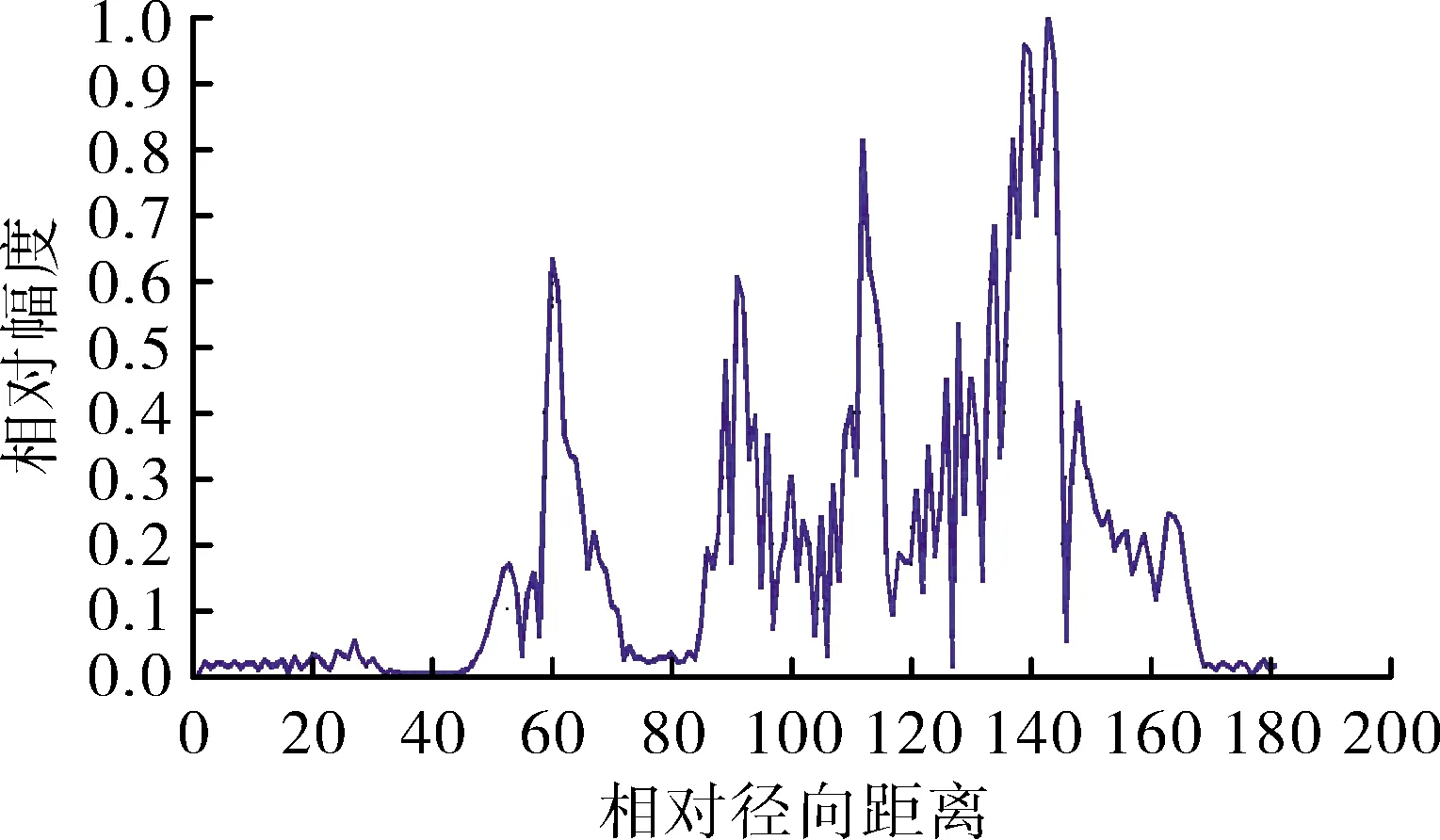
图8 方位角0°、俯仰角30°下的高分辨距离像

4 结论

研究了海面环境下电大尺寸船舰目标的电磁散射特性和高分辨距离像仿真，分析了FEKO软件仿真高分辨距离像的具体计算方法与仿真过程，对比了FEKO提供的不同仿真算法的仿真电大尺寸目标时的仿真效率，说明仿真电大尺寸目标时，高频混合算法的优越性。对船舰与海浪复合环境下的目标散射特性进行了仿真，结果表明海浪环境对船舰目标电磁散射特性有着显著的影响，因此在高分辨距离像的仿真中应充分考虑海面环境的影响。通过对海面环境下的船舰目标高分辨距离像仿真可以看出，强散射点与模型上的结构一致。因此在海面背景下仿真的高分辨距离像仍具有可行性，可以用于进行目标特征提取及目标识别。