电磁炮超高速弹丸膛内运动稳定性研究*
沈 剑,王少龙,宁益晨,陈国光,田晓丽,闫小龙
(1 中北大学机电工程学院, 太原 030051; 2 西北工业集团有限公司质量管理部, 西安 710048;3 北方华安工业集团有限公司, 黑龙江齐齐哈尔 161046)
0 引言
电磁轨道炮是利用电磁发射技术制成的一种先进的动能杀伤武器,与传统的火炮相比,有着弹丸初速高、体积小、重量轻、战场生存能力强等优势,使得它在军事领域的应用前景十分广阔[1]。电磁轨道炮所使用的弹药类型之一是超高速弹丸。BAE系统公司研制的一体化超高速射弹HVP(hyper velocity projectile),具有通用化、低风阻、可执行多任务等特点,在美军电磁轨道炮、127 mm海军舰炮和155 mm陆军榴弹炮上均可以发射,具备一定的通用性[2]。
电磁轨道炮发射环境要更加复杂,受多物理场耦合作用更加明显,弹丸在膛内运动的稳定性扰动因素更多[3]。因此,需要研究超高速弹药(含电枢、弹托和弹丸等)在电磁、热和力多场耦合作用下的运动状态。在稳定性分析领域,应用较多的是Lyapunov指数法。在工程应用方面,Tanaka等通过多Lyapunov函数的模糊来解决Takagi-Sugeno模糊系统的稳定性分析和稳定性问题[4];徐晓惠采用Lyapunov函数法和数学归纳法分析车辆纵向跟随系统的稳定性,验证了稳定性判据的合理性[5];魏军强等建立了Lyapunov函数计算电力系统随机稳定性,证明了文中构造函数方法的优势[6];张硕基于Lyapunov方法对分数阶神经网络动力学分析及控制进行了研究,并从理论和实验验证其鲁棒性[7];陈诚建立无人飞行器结构参数与系统运动稳定性之间的量化关系,以四旋翼无人飞行器起飞和偏航阶段为对象,通过实验验证理论仿真分析得到的结论[8]。
文中以超高速弹丸为研究对象,对弹丸进行动力学建模,在此基础上使用Lyapunov指数法建立起电磁轨道发射系统电流趋肤效应、膛内空气扰动、电枢与轨道间高速滑动摩擦与超高速弹药运动稳定性之间的量化关系,通过计算分析得出以上因素对弹丸运动稳定性的影响。
1 影响超高速弹丸膛内运动的因素
1.1 趋肤效应
在电磁轨道炮内发射时,作用在弹丸上的力为电枢提供的电磁推力,而电磁推力的大小主要取决于导轨的电感梯度和流经导轨的电流大小。电磁推力的表达式为:
(1)
式中:L′为电感梯度;I为导轨电流。
随着电枢的推进,弹丸沿身管轴线方向的位移递增,相应的导轨电阻和电感增加,公式如下:
Rx=R0+R′(t)x
(2)
Lx=L0+L′(t)x
(3)
式中:R0为初始电阻;L0为初始电感;R′(t)为电阻梯度。
电磁炮脉冲电源提供的电流作用时间短,电流集中于导轨和电枢的表层,产生趋肤效应。超高速弹丸速度越高,这种趋肤效应就越明显。趋肤效应造成导轨、电枢电流分布不均,产生焦耳热损失,引起电阻梯度变化[9-10]。
1.2 膛内空气阻力
弹丸在洛伦兹力的作用下沿导轨运动,此外,弹丸还受到膛内空气阻力及导轨滑动摩擦阻力作用。膛内空气阻力主要受膛内空气密度、超高速弹丸尺寸、速度和位置的影响。膛内空气阻力公式为[11-12]:
(4)
式中:γ为空气比热比;ρa为膛内空气密度;S为电枢横截面积;v为弹丸速度;x为弹丸沿身管轴向的位置;a为弹丸加速度;Cf2为空气粘滞摩擦系数;L为电枢长度。
1.3 电枢与轨道间高速滑动摩擦阻力
弹托在导轨上高速滑动,受摩擦阻力作用,滑动阻力与弹托-导轨间摩擦系数、正压力、电磁推力和空气阻力有关。
弹托在导轨上滑动摩擦阻力的公式为[13]:
(5)
式中:c为弹托-导轨滑动摩擦系数;Fp为弹托-导轨初始压力;μ为弹托材料泊松比;Sk为超高速弹丸弹底截面积;D为超高速弹丸弹径;FL为洛伦兹力。
2 HVP运动稳定性分析模型
2.1 电磁轨道炮系统方程
HVP在电磁轨道炮中的运动如图1所示。在膛内运动时,HVP受到电磁、热和力多场耦合作用,运动过程复杂,受扰动因素较多。为了更全面分析问题,文中综合考虑第一节中的各个影响参量,将HVP运动过程中的空气阻力、电枢和导轨之间的摩擦力都考虑进去,同时忽略温度对轨道和电枢的影响,并认为轨道电阻和电感与轨道接入的长度成线性关系[14]。
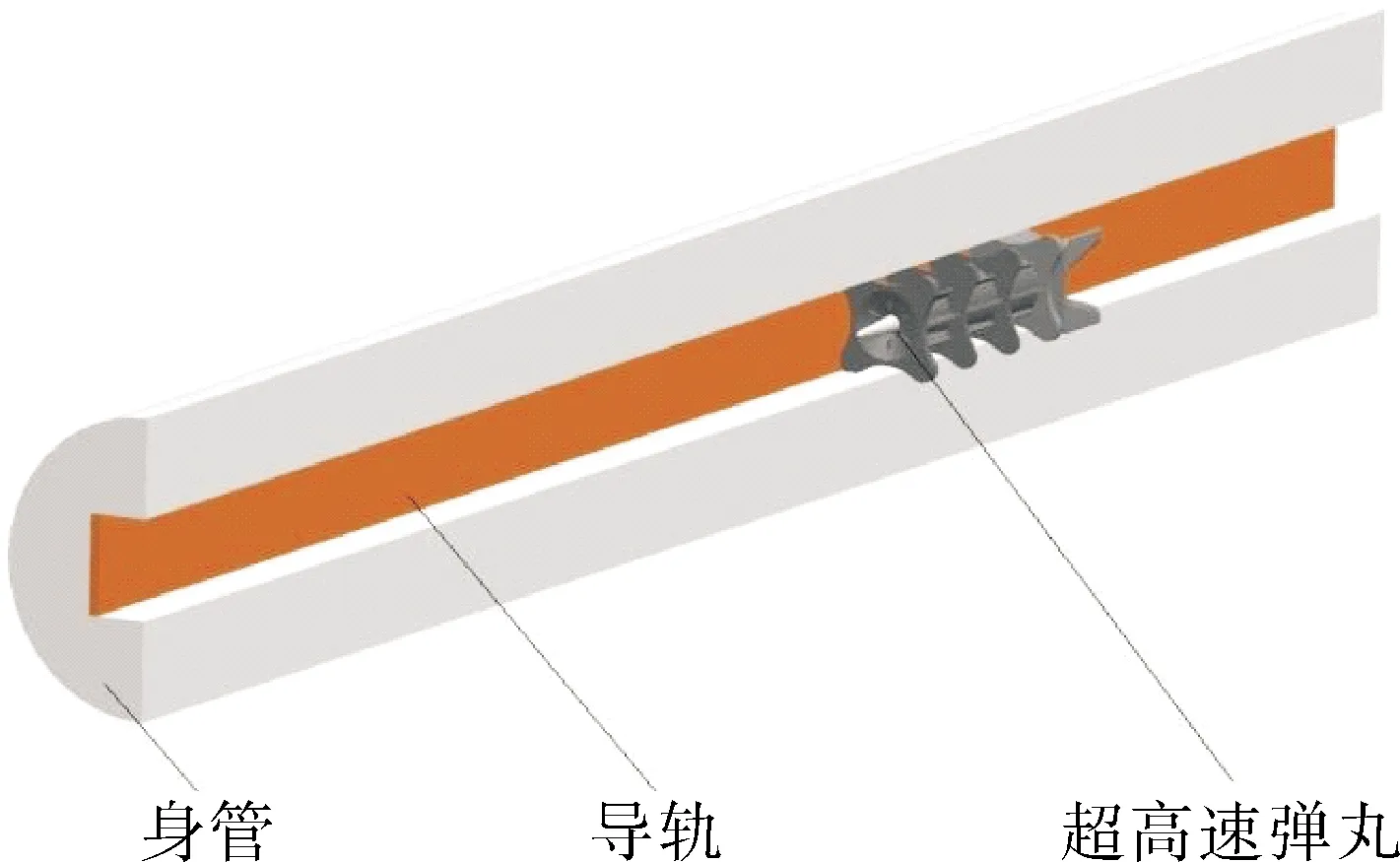
图1 HVP在电磁轨道炮中的运动示意图
建立电磁轨道炮的系统方程:
(6)
引入电流的微分方程:
(7)
式中:L′为电感梯度;R′为电阻梯度;v为弹丸速度。
引入弹丸速度、位移和电势的微分方程:
(8)
将式(1)、式(4)~式(8)联立之后得到的方程组就是电磁轨道炮总系统方程:
(9)
针对式(9)的一阶微分方程组,采用四阶龙格库塔法求解。文中采用Matlab软件编程求解电磁轨道炮的系统方程组。
2.2 Lyapunov指数法
Lyapunov指数的概念在现代非线性动力学理论中扮演着重要的角色,它是衡量系统动力学特性的一个重要定量指标,并且可以描述受干扰后的状态空间发散或收敛的平均指数率[15]。
进行动力学建模后,将得到的弹丸状态方程转化为系统的状态方程,将此状态方程代入计算方程内,就可以计算得出系统的Lyapunov指数谱。选定计算时间步长,确定迭代次数后,计算过程为:
1)在模块化的基础上构建运动学及动力学方程:
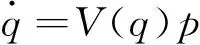
(10)

(11)
2)将动力学的方程转化为状态方程:
(12)
3)计算Jacobian矩阵得:
|df(X)/dX|Xi
(13)
4)计算Lyapunov指数谱:
(14)
其中,Lyapunov指数的大小是由函数f(X)在Xi处的雅克比矩阵|df(X)/dX|决定的,状态方程d(X)(t)/dt=f(X(t))是通过非线性系统的动力学方程得到的。
Lyapunov指数谱的符号通常被用来分析系统的运动稳定性:λ<0,说明系统趋于到达稳定状态;λ=0,系统在Lyapunov意义上表现出稳定性;λ>0,表明系统是不稳定或者混纯。
3 仿真分析
3.1 电磁炮系统仿真
根据式(9)建立的系统模型,仿真计算得到基本的电磁炮系统工作特征。计算初始参数如表1所示[14],计算结果如图2~图4所示。

表1 计算初始参数
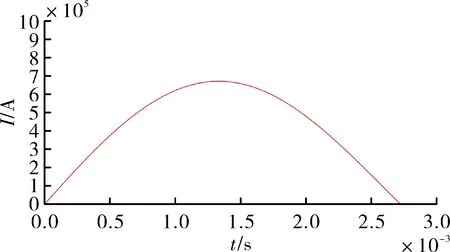
图2 导轨电流-时间曲线

图3 弹丸速度-时间曲线图

图4 弹丸位移-时间曲线图
图2、图3和图4分别是导轨电流、弹丸速度以及弹丸位移随时间变化的曲线。从以上三图可以看出:在t=1.32 ms 时,轨道电流的峰值为669.2 kA,并在t=2.71 ms时电流降为0;当t=3 ms时,弹丸恰好可以从4 m长导轨上射出;膛内运动最大速度2 396 m/s,出炮口速度2 214 m/s。
3.2 HVP膛内运动稳定性分析
根据式(10)~式(14),计算HVP膛内运动的Lyapunov指数。在3.1节计算中发现,电磁推力对弹丸运动的影响比空气阻力、滑动摩擦阻力更加明显,因此,本节仅选取电阻梯度、摩擦系数来分析参数变化对于弹丸速度、位移Lyapunov指数的影响。计算结果如图5~图8所示。

图5 电阻梯度变化对于弹丸速度Lyapunov指数的影响
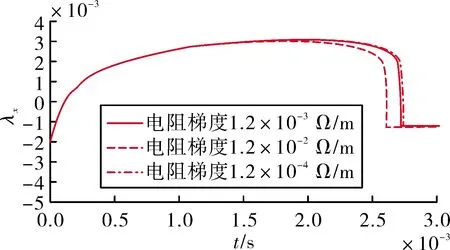
图6 电阻梯度变化对于弹丸位移Lyapunov指数的影响
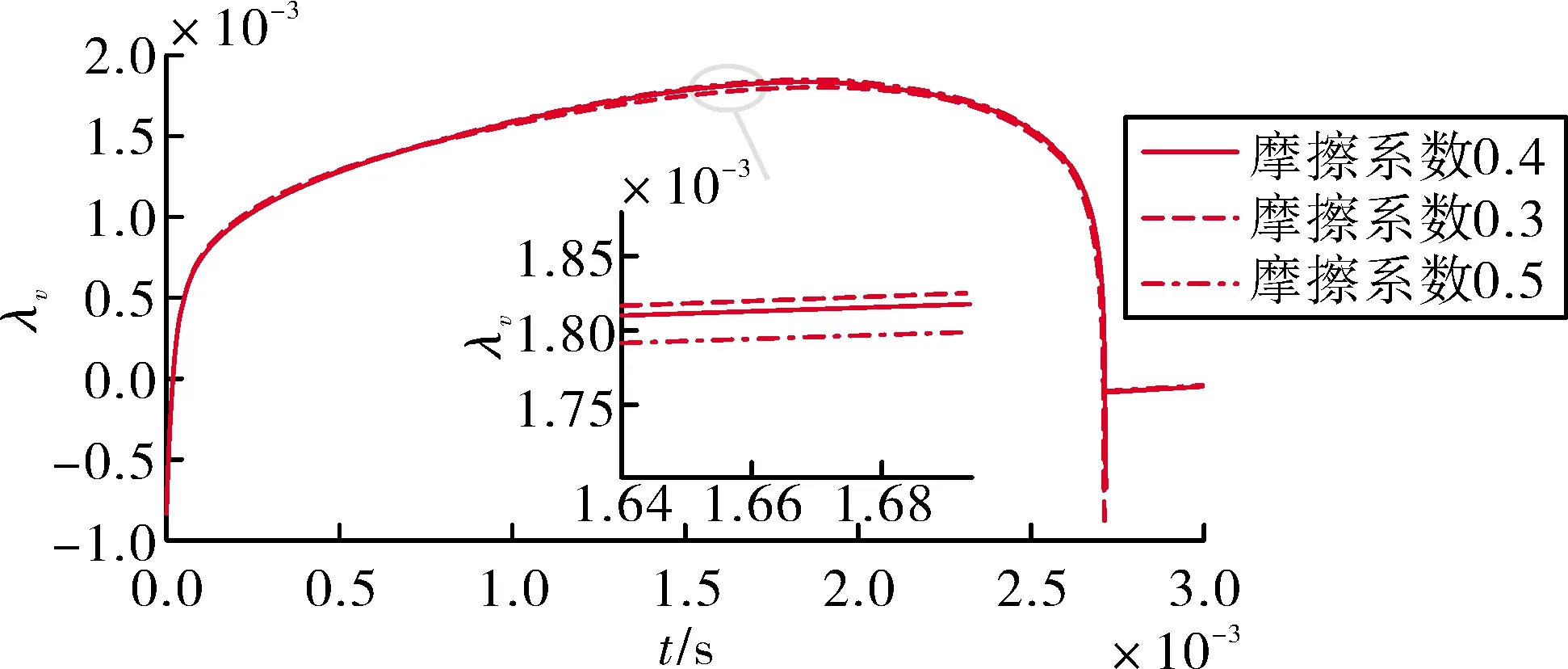
图7 摩擦系数变化对于弹丸速度Lyapunov指数的影响

图8 摩擦系数变化对于弹丸位移Lyapunov指数的影响
对比结果发现,电阻梯度的变化对弹丸运动稳定性的影响较摩擦系数变化更大。当电阻梯度增大到1.2×10-2Ω/m时,弹丸速度趋于不稳定状态;电阻梯度为1.2×10-3Ω/m时,弹丸速度趋于稳定状态;电阻梯度为1.2×10-4Ω/m时,弹丸速度处于稳定状态。电阻梯度在[1.2×10-4Ω/m, 1.2×10-2Ω/m]内变化对弹丸位移稳定性影响较小。摩擦系数在[0.3,0.5]内变化对弹丸速度、位移Lyapunov指数的影响保持在万分之一以内。
4 结论
通过分析超高速弹丸在电磁轨道炮内运动的稳定性影响因素,确定以趋肤效应、膛内空气阻力和电枢与轨道间高速滑动摩擦阻力为研究对象,分析三种因素对弹丸膛内运动稳定性的影响。建立电磁轨道炮系统动力学方程和超高速弹丸运动稳定性分析模型,通过仿真计算得到超高速弹丸在电磁轨道炮内的基本工作特征;通过调整电阻梯度和摩擦系数,计算参数变化对于弹丸速度、位移Lyapunov指数的影响。计算结果表明,电阻梯度的变化对于超高速弹丸在电磁轨道炮内运动稳定性影响明显。因此,在电磁轨道炮的研制过程中应通过一定措施控制趋肤效应对于弹丸膛内运动稳定性的影响。

