无控旋转弹丸外弹道姿态测试与模型验证

李嘉欣，沈大伟，马铁华，张煜，裴东兴

(中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051)

弹丸在飞行的过程中，由于发射条件、物理环境以及弹丸自身的设计等原因，使弹丸外弹道产生误差，影响飞行的稳定性。其中，弹丸转速及章动角成为影响弹丸飞行性能的最主要参数[1]。

随着武器技术的发展，弹丸的外形变化很大，作用在弹丸本体的各种空气动力以及力矩已经不可忽略。因此，必须考虑影响弹丸在飞行过程中所有的空气动力才能更加准确地模拟弹丸的运动姿态，通过数学模型的建立，分析弹道和射表的设计编制以及实验射程[2]。应用理想轴对称的弹丸，研究其转速和章动角的变化，从而更加准确地研究弹丸的飞行稳定性[3]。

针对以上问题，笔者提出应用MATLAB软件求解无控旋转弹丸外弹道的仿真模型，其结果与弹载测试仪现场试验结果比对，找到弹丸的运动规律，为后续的武器系统的优化设计以及新型武器的研发奠定理论基础。

1 弹丸外弹道运动姿态模型

弹丸运动时受到扰动会形成不断变化的攻角δ，当攻角增大时，导致旋转弹丸飞行不稳定，因此研究运动中弹丸的姿态以及运动规律，将弹丸视为自由运动刚体建立一个数学仿真模型[4]，分析计算其外弹道参数以及稳定性。

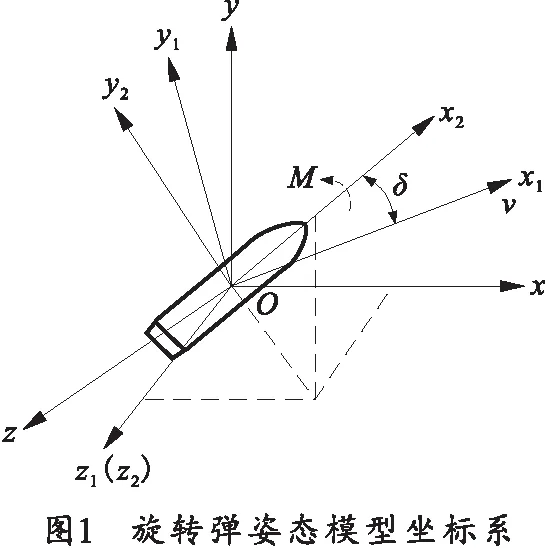
根据旋转弹丸飞行的姿态建立坐标系,如图1所示，以弹丸质心O为原点，射击方向为Ox正向，建立地面坐标系Oxyz，以速度v方向为Ox1正向，建立弹道速度坐标系为Ox1y1z1，以穿过质心弹丸轴线为Ox2正向，建立弹轴坐标系为Ox2y2z2。根据弹丸受力可将其飞行运动的物理过程分解为质心运动和绕质心转动两种形式[5]，根据建立的坐标系，列出主要运动方程。

1.1 弹丸质心运动方程

当弹丸在高速旋转时，其圆锥运动服从质心运动定理，为

(1)

式中：v为弹丸的速度；θa为速度俯仰角；θb为速度偏航角；Fx1、Fy1、Fz1分别为F在Ox1y1z1坐标轴下的分力。

1.2 弹丸绕质心运动方程

弹丸绕质心的旋转过程中，根据动量矩定理可得：

(2)

(3)

1.3 弹丸运动姿态模型

将弹丸的射程对时间t微分得到弹丸速度在地面坐标系下的分量，即

(4)

(5)

式中：δ2为偏航攻角；δ1为俯仰攻角；β为坐标系转换角[6]。

将以上弹丸质心运动方程(1),绕质心运动方程(2)、(3)，弹丸速度在地面坐标系下的分量(4),以及根据各方位角之间的关系得出的补充方程(5)联立起来就可以得到弹丸运动姿态的数学模型。

2 弹丸外弹道仿真

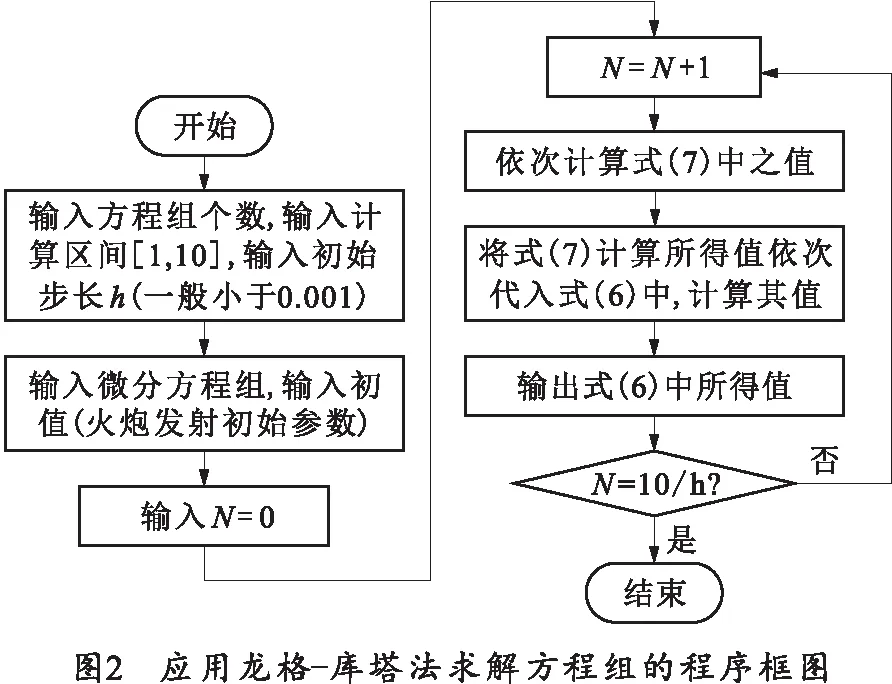
为了方便求解并提高计算精度，采用龙格-库塔法对仿真模型进行解算。

2.1 龙格-库塔法

龙格-库塔法具有精度高且稳定的特点，在工程技术上广泛应用的一种算法[7]，用于数值求解微分方程。针对弹丸运行姿态的数学模型，有

(6)

(7)

式中，点m处的值为(tm,y1n,y2n,…,ymn),参量定义详见文献[7]。

2.2 MATLAB程序的设计以及编写

应用龙格-库塔法在MATLAB软件中对微分方程进行求解，程序框图如下：

2.3 仿真结果及分析

对弹丸及环境的理想假设：

1)理想弹丸的惯性主轴为弹丸轴线且外形、质量相对于弹轴分布是对称的；

2)弹丸是静不稳定的状态；

3)地表重力加速度铅直向下，大小不变；

4)统一使用我国炮兵标准气象条件。

设置初始速度俯仰角θa=21°，速度偏航角θb=0°，初始章动角δ0=3.92°，假设弹轴俯仰角φ1=24.92°，弹轴偏航角φ2=0°，在MATLAB中仿真计算，得到转速和章动角随时间变化曲线。

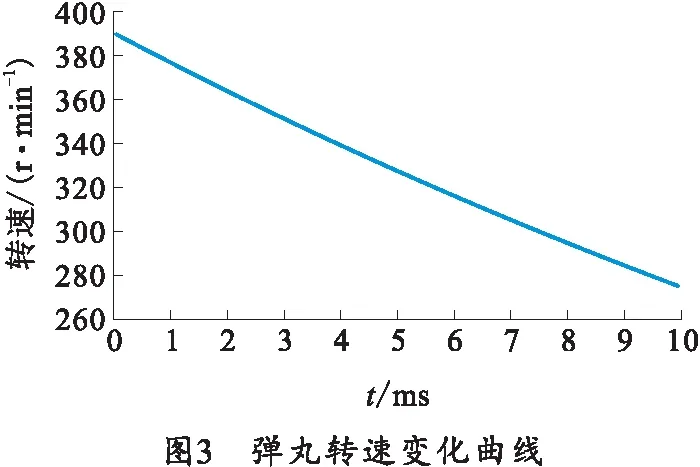
弹丸的初始转速为390 r/min，在极阻尼力矩的作用下，自转速度逐渐减小，弹丸转速变化曲线如图3所示。

弹丸的俯仰攻角以及偏航攻角的变化规律如图4所示，其峰值近似呈指数规律减小，后期减缓趋于稳定。

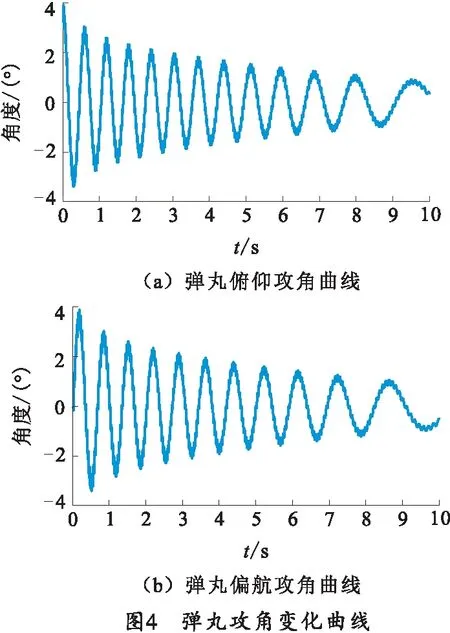
由定义可知，弹丸攻角就是弹丸章动角[8]，其弹丸的章动角变化如图5所示。

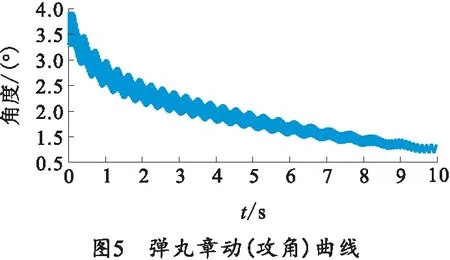
将图5的前3 s波形依次展开，如图6～8所示。1次章动运动即1个周期的变化，由图6～8可知弹丸章动周期在1、2、3 s内分别是32.5、34.0、36.0 ms，弹丸章动周期逐渐增大，飞行趋于稳定。

3 实测信号分析

3.1 弹丸的转速

弹载测试仪[9]所采集到的弹丸转速信息经滤波去噪处理后如图9所示。

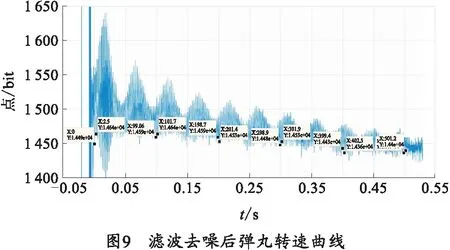
根据图9，按转速测试原理得到的实测弹丸转速值在0、1、2、3 s时刻分别为390.0、378.8、370.4、344.8 r/min。

3.2 弹丸的章动角

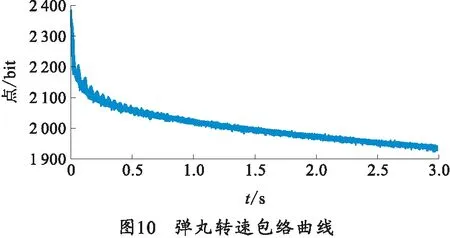
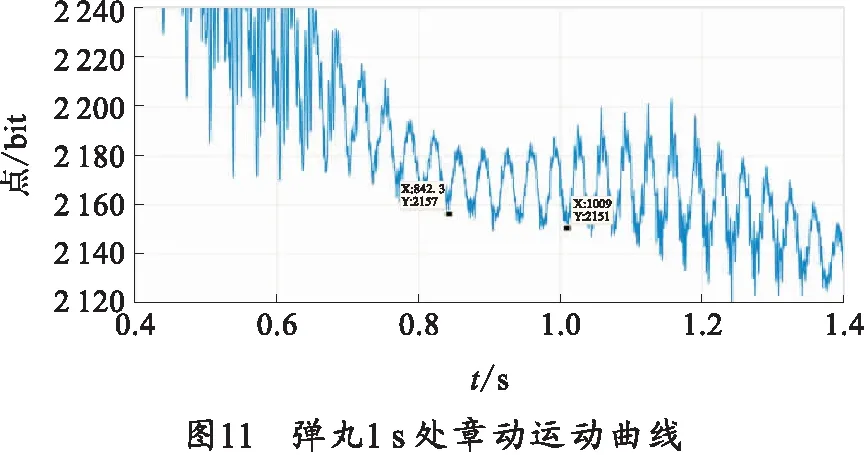
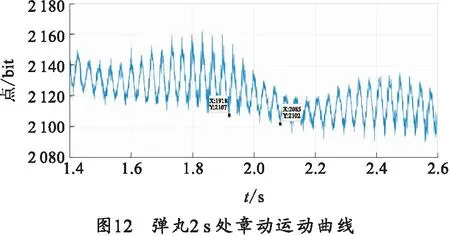
提取图9中转速曲线中包络线，如图10所示，包络线中波动就代表弹丸的章动运动。根据T=t/n对滤波后的曲线进行解算即可得到弹丸在飞行过程中的章动周期[10]。将图中信号分别在1、2、3 s附近展开，如图11～13所示。数据表明弹丸章动在第1、2、3 s内的周期分别是33.34、33.40、33.8 ms。

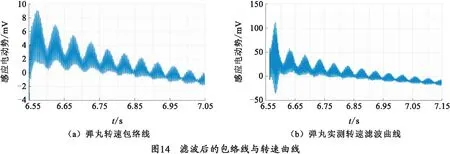
滤去无效信号，通过计算获得弹丸在不同时刻的章动角。根据测试仪不同时刻的输出(mV)及对应转速，可得图14，弹丸在出炮口时刻的地磁感应电动势为E=56 mV，弹丸章动变化的电动势为ΔE=6.5 mV，弹丸轴线与当地地磁场之间的夹角为30°，弹丸在刚出炮口时两电动势之间有如下关系[8]：

(8)

根据式(8)可以计算得出弹丸刚出炮口时刻的章动角δ=3.92°。依次求解出弹丸在1、2、3 s时的章动角分别为2.464°、2.329°、2.205°。

将弹丸转速、章动角、章动周期的仿真结果与弹载测试仪实测进行对比，如图15所示。

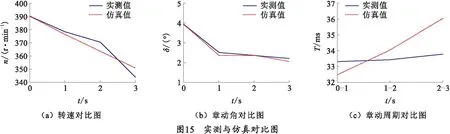
通过对图15的数据计算，可得到仿真值与实测值误差在10%以内，相关系数均大于0.94，因此所建立的弹丸外弹道运动姿态仿真模型是合理可行的。

4 结束语

笔者以无控旋转弹丸为主体，建立了外弹道数学模型，并基于MATLAB软件对弹丸的运动飞行姿态进行了仿真分析，得到了转速和章动曲线，并将速度、章动角以及章动周期与实测数据进行对比，所得结果基本一致，验证了笔者所建立姿态模型的合理性。