水下炮弹水弹道特性仿真研究

袁军，王卫，李瑞杰

(1.海军装备部，陕西 西安 710025；2.西北机电工程研究所，陕西 咸阳 712099)

近些年来，随俄罗斯“暴风雪”号超空泡鱼雷、美国机载快速灭雷系统、挪威多环境弹药的相继问世，将超空泡技术在水中兵器的应用推向了新高度[1-4]；同时面对水雷、鱼雷、UUV、蛙人装备的快速发展，水下防御能力急需加强。基于水下发射技术、超空泡射弹技术的日趋成熟，开展基于超空泡减阻技术的水下炮弹技术研究变得十分必要。因水下炮弹具有反应快、成本低、可高效打击水下目标等特点，水下炮弹技术研究的必要性日益增强[5-7]。笔者借助数值模拟、弹道仿真方法对水下炮弹的空泡特性和水弹道特性进行研究[8-9]。

1 水下刚体弹道方程组模型

笔者研究的水下炮弹的弹径为76 mm，弹长为396 mm，弹质量为5.2 kg，空化器直径为20 mm，在无动力航行中，自空化器边缘形成自然空泡，空泡基本将水下炮弹包裹，不考虑水的流速，在静水环境下弹丸所受的作用力主要包括重力、空泡内气动力、水动力，由于空泡内气动力、水动力中的阻尼力及力矩、马格努斯力及力矩相较于水动力中位置力及静力矩在量级上要小两个数量级以上，水动力中位置力及静力矩对于水下炮弹的作用要远大于其他力及力矩作用，因此笔者只考虑重力及水动力中位置力和静力距效应，其他力及力矩忽略不计。水中航行受力如图1所示，水下炮弹弹丸速度为v，弹丸转速为wx，弹丸攻角为α，弹丸未穿刺空泡时，弹丸受自身重力G及空化器处水的阻力Fα；在较大攻角情况下，弹丸产生沾湿，沾湿部位受到水的径向回复力Fmd，轴向阻力Fml及周向阻力Fmp。

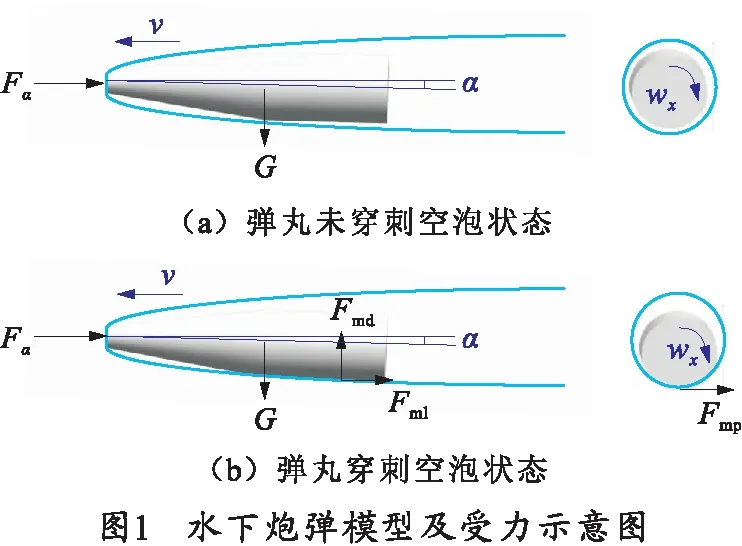
根据动量定理和动量矩定理，将前述作用力向弹道坐标系投影，作用力矩向弹轴坐标系投影即可得到水下炮弹弹丸动力学方程组的一般形式为

(1)

矩阵AD为

(2)

弹丸质心平移运动方程组为

(3)

式中:x,y,z为弹体质心位移在地面坐标系下的分量;θα为速度高低角；ψ2为速度方位角。

弹丸转动运动方程组为

(4)

高低攻角δ1、方向攻角δ2及侧滑角β三者之间的关系式为

sinδ2=cosψ2sinφ2-sinψ2cosφ2cos(φa-θa),

(5)

sinδ1=cosφ2sin(φa-θa)/cosδ2,

(6)

sinβ=sinψ2sin(φa-θa)/cosδ2,

(7)

式中，φa为弹轴高低角。

式(1)～(7)构成了闭合的水下炮弹刚体弹道方程组，获得全部水动力系数即可予以求解。

2 水动力系数数值模拟求解

2.1 数值模拟模型的建立

基于VOF模型对雷诺时均方程组进行求解。基本控制方程包括连续性方程和动量方程：

(8)

(9)

式中：下标i和j分别表示坐标轴方向；u和p分别为速度和压强；μt为涡旋黏性系数；μm和ρm分别为混合物的动力黏性系数和密度：

μm=αrμv+(1-αr)μ1,

(10)

ρm=αrρv+(1-αr)ρ1,

(11)

式中：αr为蒸汽体积率，用来反映水-汽两相之间的相变；下标v、l分别表示汽相和水相。

选用剪切应力传输(SST)k-ω模型，该湍流模型对壁面切应力计算准确，计算结果相对稳定。k方程和ω方程的形式为

(12)

(13)

式中：k为湍流动能；ω为湍流频率；Γk、Γω为湍流扩散系数；Gk、Gω为湍流生成项；Yk、Yω为湍流动能耗散项；Sk、Sω为自定义项。

基于质量传输的空化模型，忽略热传输和非平衡相变效应，采用组分传输方程描述液相体积含量的输运方程为

(14)

采用Schnerr and Sauer模型，该空化模型将汽相体积分数和单位体积流体内空泡数量相联系，表达式为

(15)

(16)

式中：ρw为水密度；αc为气核体积分数；RB为气核空泡直径；n为单位体积空泡数量。

2.2 数值模拟模型的验证

数值模拟模型的验证采用数值模拟的空泡形态及空泡尺寸与经典试验对比的方法。笔者研究对象的设计初速为900 m/s，选用经典试验的弹丸速度为970 m/s，二者速度相差在10%以内，且均处于水中亚声速范围内，可通过空泡形态及尺寸的对比验证数值模拟模型对研究对象在设计速度下的适用性。图2为相同弹丸外形、相同速度下的经典试验空泡和数值模拟空泡对比图。

对比结果显示数值模拟空泡形态与试验空泡较为接近，轴向距离0～225 mm内仿真空泡与试验空泡轮廓径向尺寸的最大相对误差不大于5%，能够反映真实的物理事实和流场信息。以下沿用该数值模拟模型对水下炮弹的空泡形态及水动力参数进行求解分析[10-11]。

2.3 水动力系数的求解

对水下炮弹900 m/s速度下水中航行过程进行数值模拟，水下炮弹空泡形态如图3所示，α为攻角。结果显示，弹丸攻角超过1.5°，弹丸锥面将产生沾湿，且沾湿面积随攻角增大而大幅增大。

水动力系数通过对水下炮弹在给定攻角范围、给定转速范围内设定离散工况定常仿真水动力，并进行水动力与水动力系数换算及曲线拟合来获得。对水下炮弹在900 m/s初速下，转速为4 000～8 000 rad/s，攻角为-3°～3°条件内选取工况进行定常数值模拟并监测弹丸的阻力、升力、侧向力、俯仰力矩、偏航力矩及滚转力矩。

阻力系数曲线如图4所示，阻力系数在±1.5°攻角内变化较小，弹芯攻角一旦超过±1.5°，弹身发生沾湿，阻力系数变化急剧增大。

根据最小二乘准则采用分段函数的方法拟合获得的阻力系数函数如式(17)所示。

(17)

升力系数曲线如图5所示，根据最小二乘准则采用分段函数的方法拟合获得的升力系数函数如式(18)所示。

(18)

侧向力系数cz求解结果如图6所示，拟合获得的侧向力系数cz的导数函数如式(19)所示。

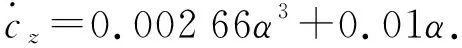
(19)

滚转力矩系数mx求解结果如图7所示。根据最小二乘准则采用分段函数拟合获得的滚转力矩系数mx的导数函数如式(20)所示。

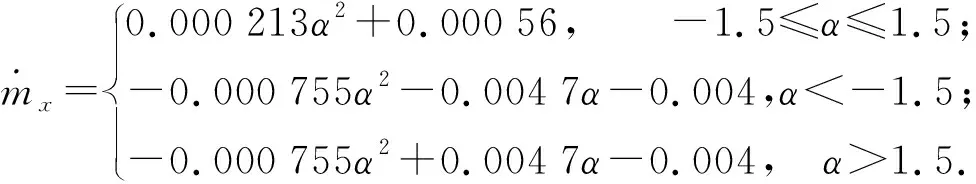
(20)

俯仰力矩系数曲线如图8所示。根据最小二乘准则采用三次函数的形式对数据拟合获得的俯仰力矩系数函数如式(21)所示。

mz=0.003 77α3-0.014 3α.

(21)

偏航力矩系数my求解结果如图9所示。采用三次函数对数据拟合获得偏航力矩系数my的导数函数如式(22)所示。

(22)

将式(17)～(22)代入水下炮弹刚体弹道方程组，即可进行弹道解算。

3 水下炮弹水弹道特性分析

以初速v=900 m/s，高低攻角δ1=1°，转速ωξ=8 000 rad/s，其余变量初始值为0的初始条件对水下炮弹刚体弹道方程组进行解算，可得到弹丸的速度-航程曲线、转速-航程曲线，如图10、11所示。计算结果显示，弹丸水中航程100 m处存速为105 m/s，转速为6 310 rad/s。

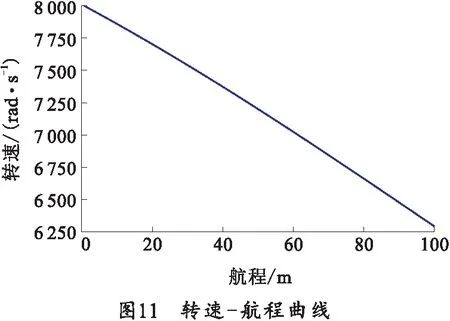
图12给出了水下炮弹的高低攻角-方向攻角复平面曲线，分析可知，在有限时间内水下炮弹的相对攻角增速很小，振幅较小，相对攻角随时间的变化在复平面内形成规则圆形。

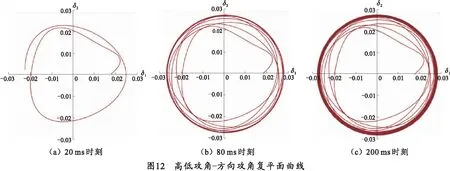
根据弹箭的非线性运动稳定性理论，并结合俯仰力矩表达式(21)可知，水下炮弹在俯仰力矩作用下表现为小攻角稳定、大攻角失稳。水下炮弹水中运动稳定的充分条件为

(23)

式中:M0和M2为非线性力矩对攻角的一次项系数和三次项系数；δm和δn为水下炮弹运动时的攻角最大值和攻角最小值。

取攻角最大值为δ，攻角最小值为0，将式(21)中的系数代入式(23)，可得水下炮弹的攻角稳定域为|δ|<1.3°。

4 结束语

笔者建立了水下刚体弹道方程组，数值模拟了水下炮弹在水中航行过程的空泡形态并求解了相应的水动力系数，对900 m/s初速、8 000 rad/s转速的水下炮弹进行了弹道仿真，结果显示，弹丸可航行100 m，存速大于100 m/s，转速下降约20%。此外，弹丸发生沾湿的临界攻角为1.5°，为保证弹丸稳定航行，初始攻角应小于1.3°。