高平机特性对弹丸起始扰动的影响分析

胡坚江，顾克秋

(南京理工大学 机械工程学院，江苏 南京 210094)

某轻型牵引火炮配置了螺杆气压式高平机。高平机集合了火炮高低机与平衡机功能，起着调节火炮高低射角、平衡起落部分重力矩的作用。高平机的平衡特性以及高低机螺杆-螺母接触支撑特性与弹丸膛内时期火炮起落部分动态行为具有耦合关系，将影响到弹丸出炮口状态。因此，对该问题进行分析研究对于火炮高平机的设计和使用具有现实意义。

现有研究与文献表明火炮结构接触/碰撞特性是影响火炮射击精度的原因之一[1]。在火炮发射动力学领域，许多学者[2-3]对影响射击精度的因素进行了大量分析研究；同时部分学者也将高平机作为分析对象，研究其对火炮射击精度的影响。例如张志军[4]研究了某液体气压式高平机刚度对某车载火炮弹丸起始扰动影响规律，研究结果表明，增大高平机刚度，对减小起始扰动有利；李强[5]分析了某机械式高平机刚度对弹丸起始扰动影响规律；以上研究都是以连接器等效刚度形式替代高平机模型，这种处理方法难以精确模拟高平机结构接触特性对弹丸起始扰动的影响。崔凯波等[6]分析了某高低机传动间隙对炮口扰动影响规律；曾晋春等[7]分析了某火炮高低机主齿轮之间的接触/碰撞对炮口扰动影响；以上研究都是以多刚体动力学进行分析，同时炮口扰动与弹丸起始扰动不具有一致性，构建全柔体弹炮耦合模型分析弹丸起始扰动相比于利用多刚体动力学分析炮口扰动更具有实际意义。

笔者通过构建全柔体弹炮耦合模型并考虑高平机各部件接触作用，研究高平机的平衡特性以及高低机螺杆-螺母接触支撑特性对弹丸起始扰动的影响，为高平机的设计优化和使用提供参考。

1 高平机平衡特性分析

1.1 高平机结构原理

某螺杆气压式高平机，其结构示意图如图1所示。

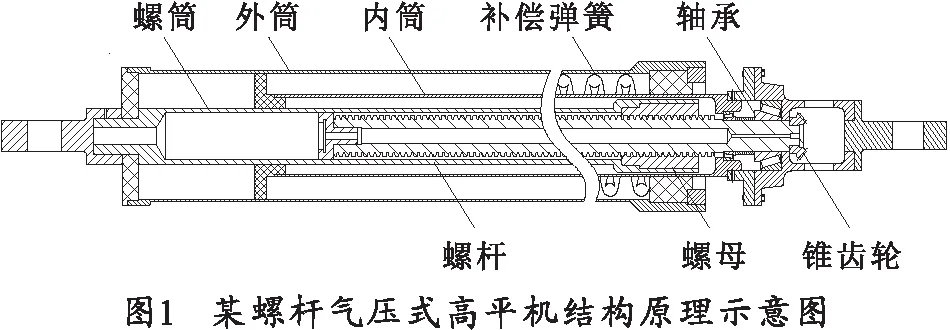
螺杆气压式高平机利用螺杆螺母及传动部件将旋转运动调整为内外筒的直线运动达到了调整火炮高低射角的功能，利用气体压强克服起落部分重力矩实现平衡机功能。高平机采用左右对称布置在两侧，同时与外部储气筒相连，保证其气压的一致性。安装补偿弹簧的目的是考虑在大射角状态下高平机所受不平衡力矩较大。当达到一定射角后，补偿弹簧才开始压缩产生弹簧力矩用以抵消部分不平衡力矩，达到了减小手轮力的目的。

1.2 高平机平衡特性

高平机受力模型二维简图如图2所示，x轴方向为水平，y轴方向为竖直，O点为耳轴的中心位置点。

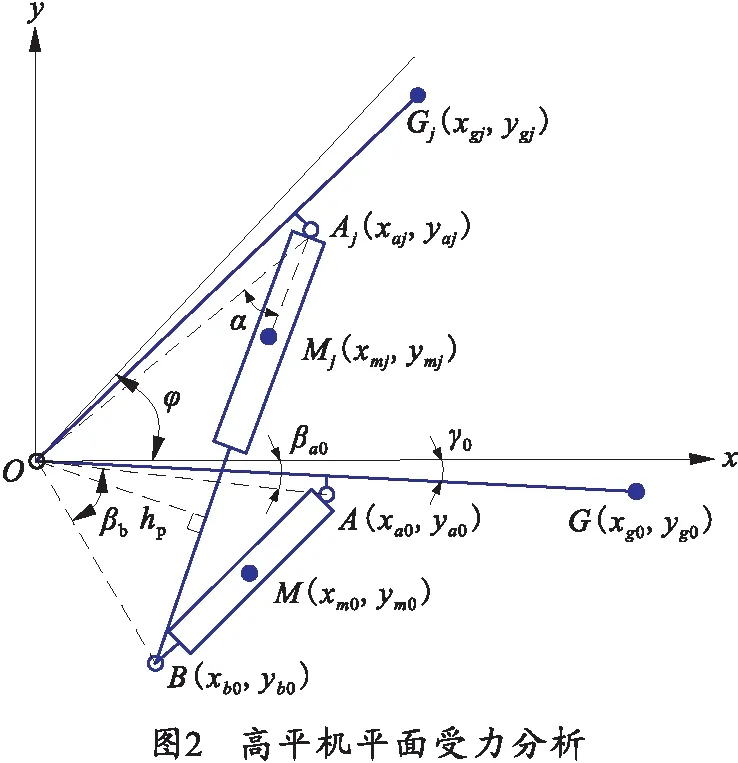
图2坐标系中，O点坐标为(0,0)；A点为高平机上支点，坐标为(xaj,yaj)，下标j表示不同射角，初始值是指j=0，即0°射角状态时的位置；B点为高平机下支点，坐标为(xbj,ybj)；G为火炮起落部分质心，坐标为(xgj,ygj)，质量为m1；M为高平机筒侧部件质心点，坐标为(xmj,ymj)，质量为m2；φ为射角，射角范围为-3°～65°；hp为高平机作用力臂；LOA、LOB、LOG分别为O点至A、B、G点的距离值。

1.2.1 相关参数数值计算表达式

由图2可知：

(1)

(2)

(3)

式中：Lj为高平机上下支点AB间的距离；βb为0°射角时OA与OB夹角；α为OA与AB夹角；S为高平机活塞工作面积；dp为高平机内筒外径；dn为高平机螺筒外径。

1.2.2 火炮起落部分重力矩

由于起落部分质心与高平机筒侧质心变化不相同，故需要分两部分对重力矩进行计算。

Mq=m1gh1+m2gh2，

(4)

h1=LOGcos(φ-γ0)，

(5)

式中：Mq为在不同射角下的重力矩；h1为火炮起落部分质心与O点的水平距离；h2为筒侧质心与O点的水平距离；γ0为OG与x轴夹角。

1.2.3 高平机气压平衡力矩

hp=LOAsinα，

(6)

Fp=Scpj=Scp65(V65/Vj)n，

(7)

Vj=V65-S(L65-Lj)，

(8)

Mp=2Fphp，

(9)

式中：Fp为高平机气压力；c为气体压强系数；pj为压强值；Vj为高平机气室体积；V65为高平机在65°射角下的气室体积；n为气体多变指数，大小为1.05；L65为高平机在65°射角下A点至B点距离；Mp为高平机气压总力矩。

1.2.4 高平机补偿弹簧力矩

补偿弹簧仅在达到一定射角才进行压缩来补偿不平衡力矩，未达到补偿射角时不起补偿不平衡力矩的作用。判断补偿弹簧是否起作用，可通过折算高平机上下支点距离进行判断：

(10)

式中：MT为补偿弹簧力矩；k0为补偿弹簧刚度；Lc为弹簧被压缩时的高平机上下支点距离。

1.2.5 紧塞密封装置摩擦力矩

摩擦力矩Mf：

Mf=2Ffhp，

(11)

Ff=(f1πdpl1+f2πdnl2)pj+Fm，

(12)

式中：f1和f2为摩擦系数；l1为内筒部分与橡胶圈接触长度；l2为螺筒部分与橡胶圈接触长度；Fm为单个高平机活塞摩擦力，大小为500 N。

1.2.6 高平机不平衡力矩

不考虑摩擦力的情况下，不平衡力矩为

ΔM=Mp-MT-Mq.

(13)

在考虑摩擦力的情况下，分为高低射角增大与高低射角减小两种情况：

高低射角增大，不平衡力矩为

ΔMu=Mp-MT-Mf-Mq.

(14)

高低射角减小，不平衡力矩为

ΔMd=Mp-MT+Mf-Mq.

(15)

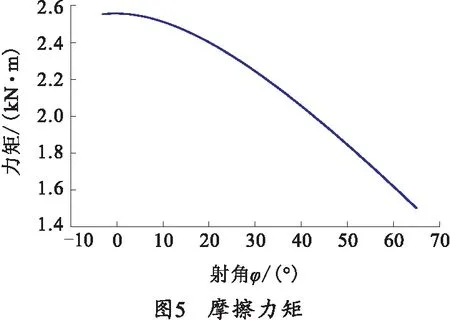
通过分析高平机受力，将高平机设计参数代入，编写计算程序得出在不同射角状态下高平机所受重力矩、平衡力矩、不平衡力矩，摩擦力矩，计算结果如图3～5所示。

1.3 螺杆-螺母接触支撑特性

现有结构参数设计中，高平机气体压强系数c=1。经过计算，当0.96≤c≤1.02时，在火炮射角范围-3°～65°内摩擦力矩能平衡不平衡力矩，高平机系统处于相对平衡状态，即动摩擦力矩大于不计摩擦不平衡力矩。

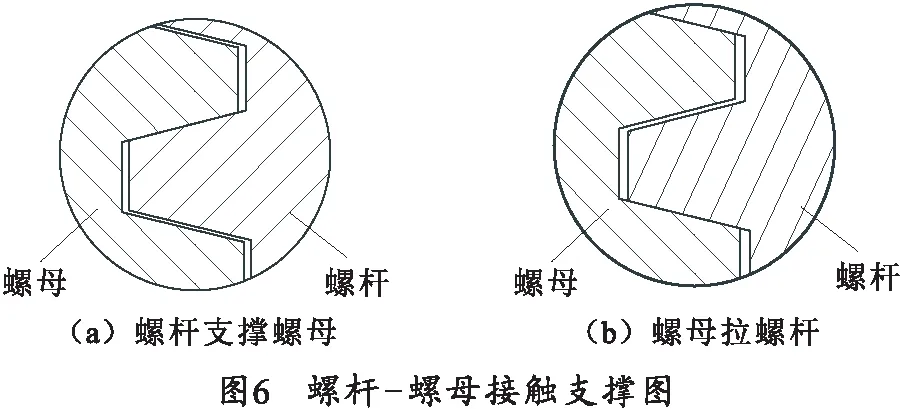
为了分析高平机螺杆-螺母接触支撑特性对火炮射击密集度的影响，对射击前高平机操作定义两种状态：“向上排空回”定义为炮手操瞄时从低射角向高射角打手轮至目标射角；“向下排空回”定义为炮手操瞄时从高射角向低射角打手轮至目标射角。向上排空回时，螺杆支撑螺母，反之向下排空回时螺母拉螺杆，如图6所示。当摩擦力矩足够大时，摩擦力矩能平衡不平衡力矩。

2 有限元弹炮耦合动力学建模

2.1 建模基本假设

由于火炮在发射过程中弹带挤进、弹丸与身管接触作用机理都十分复杂，目前对弹炮耦合研究无法完整精确构造整个过程，基于计算和建模技术等因素综合考虑，对此次建模做出如下几点假设：

1)忽略弹带部分挤进膛线的过程，假设初始状态下的弹带已完全挤入膛线；

2)忽略燃烧产生的高温对弹丸在膛内运动造成的影响作用；

3)不考虑炮口制退器流场带来的影响；

4)不考虑火药气体后效作用对弹丸的运动过程所带来的影响。

2.2 弹炮耦合有限元动力学建模

根据假设情况忽略弹带的挤进过程，即弹带上已刻画与膛线接触的弹痕，身管是先利用Pro/E构建带有膛线的实体模型，再利用Hyper mesh扫描映射功能构造六面体网格，对其划分相对规则的网格模型，划分完网格之后的身管、弹带和弹丸有限元模型装配体如图7所示。

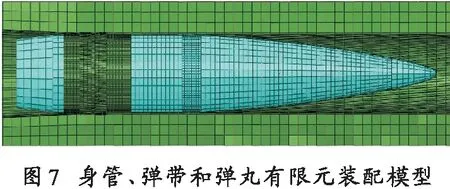
某轻型牵引火炮是由下架、前后大架、上架、摇架、高平机、后坐体、反后坐装置、瞄准、供输弹、行军装置等辅助配件组成。先对构建好的三维模型进行一定的修改，对后坐体进行一定简化，然后导入到ABAQUS中，用参数化土壤模型替代实体土壤模型。高平机摩擦力及反后坐装置利用ABAQUS程序语言接口实现二次开发，根据制退机、复进机、高平机相关特征参数编制函数程序，以连接器模式实现力、位移、速度的传递，同时考虑重力场的作用。

在火炮发射过程中，弹丸在膛内作用时间仅十多毫秒，具有瞬态、强非线性等特点。在求解弹炮耦合有限元动力学模型时，使用混合求解的方法能发挥有限元显式和隐式求解各自的优势，弹炮耦合有限元动力学模型如图8所示。

3 高平机特性对弹丸起始扰动的影响

3.1 弹丸起始扰动评价函数

以弹丸回转和俯仰方向出炮口时刻的速度、角速度与角位移为特征变量，对表征弹丸起始扰动的3个特征变量进行加权处理，构建弹丸起始扰动的评估函数[8-10]：

F=fVD+fHD，

(16)

(17)

(18)

式中：fVD，fHD分别为回转方向和俯仰方向的评估函数；θz，θy分别为弹丸回转与俯仰方向角位移；ωz，ωy分别为弹丸回转与俯仰方向角速度；vz，vy分别为弹丸回转与俯仰方向速度；θz0，θy0，ωz0，ωy0，vz0，vy0分别为各参数绝对值的平均值；α1+α2+β1+β2+γ1+γ2=1，其中α1，α2为0.125，β1，β2为0.25，γ1，γ2为0.125。

3.2 接触支撑特性对弹丸起始扰动的影响

为分析螺杆-螺母接触支撑特性对弹丸起始扰动影响，分别构建0°与48°弹炮耦合有限元模型，通过调整气体压强系数c,计算典型射角0°与48°下弹丸出炮口时运动状态参数特征，然后经加权处理计算其弹丸起始扰动评估函数值。

3.2.1c=0.75

当c=0.75时，在0°与48°射角下，摩擦力矩无法平衡不平衡力矩，分别计算0°与48°射角下螺杆- 螺母两种接触支撑状态下弹丸起始扰动评估值，所得结果如表1所示。

表1 c=0.75时弹丸起始扰动评估值

由表1可知，在0°与48°射角下，当气压变化系数c=0.75时，摩擦力矩不足以平衡不平衡力矩。两种状态下弹丸起始扰动评估值基本相等，主要原因是在受各力矩作用后，螺母拉螺杆的接触支撑状态会变为螺杆支撑螺母，故两种状态下弹丸起始扰动评估值相近。

由图9、10弹丸在膛内运动参数曲线图，反应出两种接触支撑状态下弹丸在膛内运动参数曲线基本重合，表明在发射过程中，两种状态下弹丸动态响应的一致性。

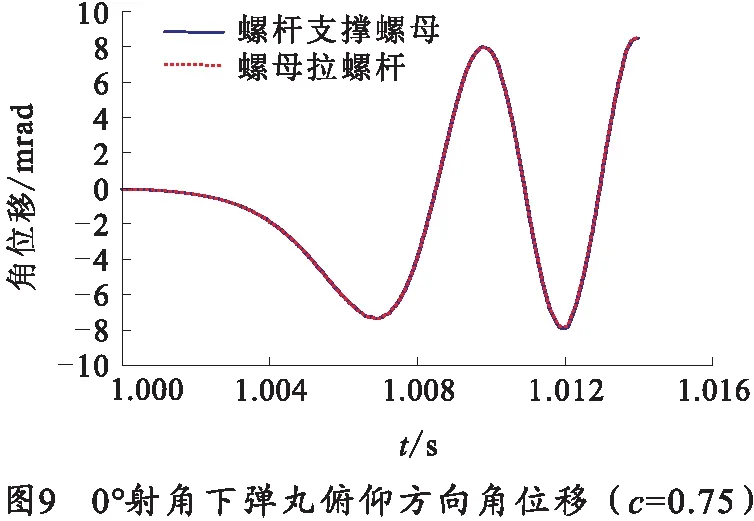
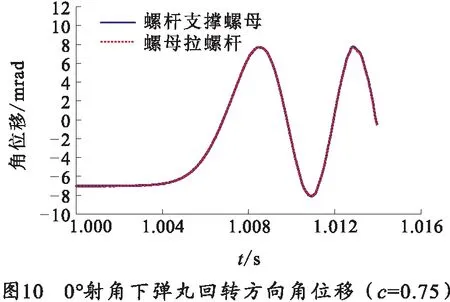
3.2.2c=0.96

当c=0.96时，高平机在0°与48°射角都处于相对平衡状态，静摩擦力矩能平衡不平衡力矩，计算0°与48°射角螺杆-螺母两种接触支撑状态下弹丸起始扰动评估值，计算结果如表2所示。

由表2可知，在0°与48°射角下，当气压变化系数c=0.96时，静摩擦力矩能够平衡不平衡力矩，螺杆支撑螺母状态下的弹丸起始扰动评估值要小于螺母拉螺杆状态下的值。

表2 c=0.96时弹丸起始扰动评估值

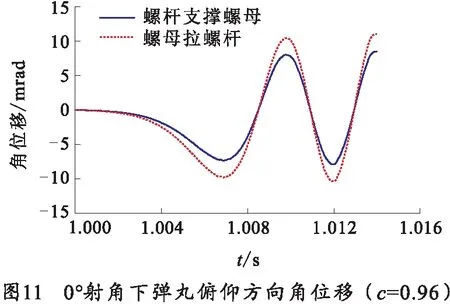
由图11、12弹丸在膛内运动参数曲线图，能反应出螺杆支撑螺母状态下的弹丸在膛内振幅小于螺母拉螺杆状态下的弹丸在膛内振幅。

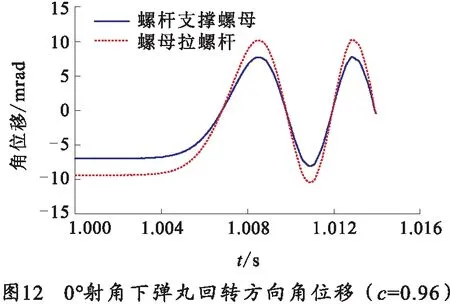
3.2.3c=1.02

当c=1.02时，高平机在0°与48°射角都处于相对平衡状态，静摩擦力矩能平衡不平衡力矩，对比螺杆支撑螺母与螺母拉螺杆两种状态下弹丸起始扰动评估函数值，计算结果如表3所示。

表3 c=1.02时弹丸起始扰动评估值

由表3可知，在0°与48°射角下，当气压变化系数c=1.02时，螺杆支撑螺母状态下的弹丸起始扰动评估函数值要小于螺母拉螺杆状态下的值；这与c=0.96时规律一致，反映了当高平机系统摩擦力矩大于不计摩擦不平衡力矩即高平机处于相对平衡状态时，螺杆支撑螺母状态下对减小弹丸起始扰动有利。

由图13、14弹丸在膛内运动参量曲线图，能反应出螺杆支撑螺母状态下的弹丸在膛内振幅小于螺母拉螺杆状态下的弹丸在膛内振幅。

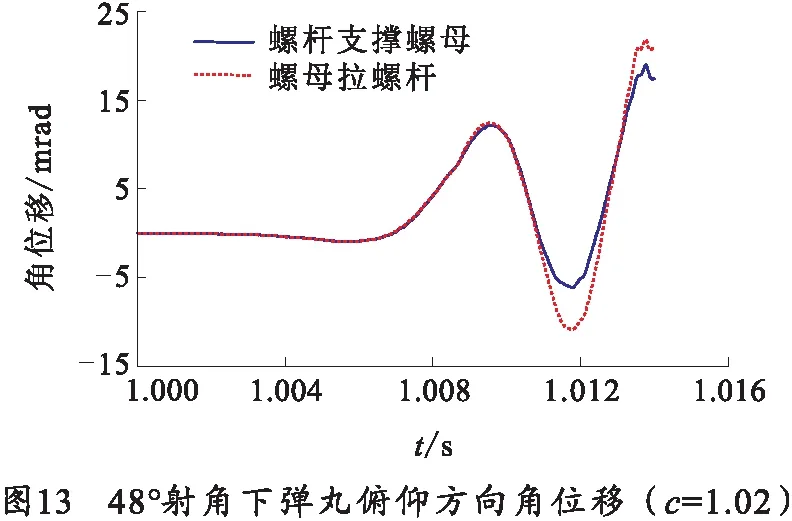
3.2.4c=1.25

当c=1.25时，在0°与48°射角下，摩擦力矩无法平衡不平衡力矩，分别计算0°与48°射角螺杆-螺母两种接触支撑状态下弹丸起始扰动评估值，所得结果如表4所示。

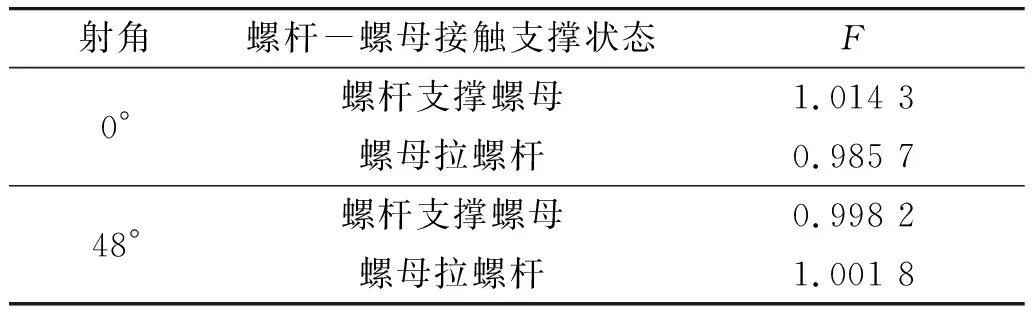
表4 c=1.25时弹丸起始扰动评估值

由表4可知，在0°与48°射角，当气压变化系数c=1.25时，摩擦力矩不足以平衡不平衡力矩，螺杆支撑螺母与螺母拉螺杆两种状态下弹丸起始扰动评估值相近，原因在于当动摩擦力矩小于不计摩擦不平衡力矩时，螺杆支撑螺母的状态会变成螺母拉螺杆的状态，故两种状态下弹丸起始扰动评估值相近。

由图15、16弹丸在膛内运动参数曲线，能反应出螺杆支撑螺母状态下弹丸在膛内运动状态与螺母拉螺杆状态下完全一致，两种状态下弹丸在膛内运动曲线完全重合。

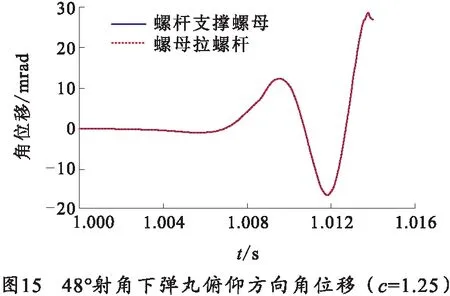
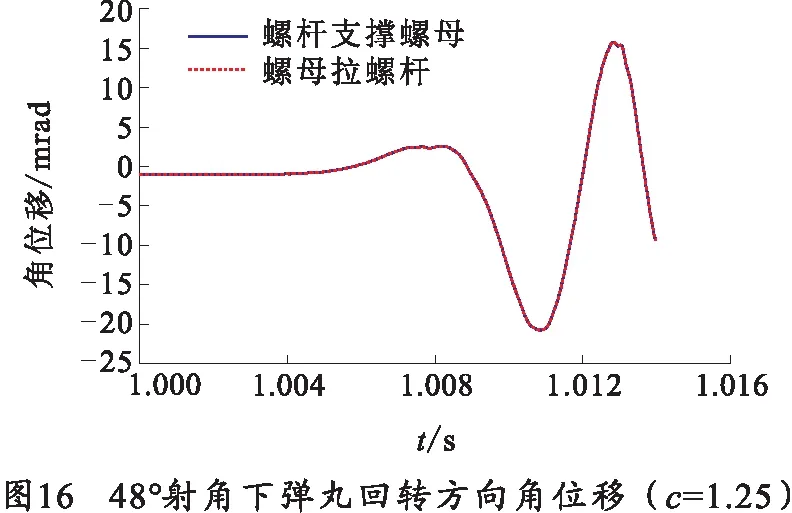
以上分析结果表明，当高平机系统处于相对平衡状态时“螺杆支撑螺母”状态下更有利于减小弹丸起始扰动，有利于提高射击密集度。这个研究结果也得到了样机靶场试验结果的支持。

3.3 平衡特性对弹丸起始扰动的影响

高平机平衡特性主要受气体压强影响，为分析平衡机气体压强对弹丸起始扰动影响规律，采用控制单一变量变化法，计算气压系数0.3≤c≤0.9范围内起始扰动评估值。以上范围内高平机处于不平衡状态，需要依靠螺杆-螺母相互接触支撑作用平衡不平衡力矩，分别计算0°与48°射角下弹丸起始扰动评估值，计算结果如图17所示。

由图17目标评估函数值曲线可看出，随着气体压强系数减小，弹丸起始扰动评估函数值也在减小，这反映了气压的减小对降低弹丸起始扰动有利。

以上分析表明了0°射角与48°射角高平机气体压强对弹丸起始扰动影响规律的一致性，即高平机气体压强越小，对弹丸起始扰动影响越小。

4 结论

针对某螺杆气压式高平机平衡特性以及高低机螺杆-螺母接触支撑特性对弹丸起始扰动的影响，通过应用有限元构建全炮弹炮耦合动力学模型，提取弹丸在膛内运动参数，主要结论如下：

1)高平机系统处于平衡状态时，螺杆支撑螺母状态下弹丸起始扰动较小；高平机气体压强越小，对弹丸起始扰动影响越小。

2)本文研究内容和分析方法针对于研究弹丸起始扰动具有一定参考价值，同时研究结果对于指导该型火炮设计优化和试验有一定参考意义。