基于RBF 神经网络PID 控制的高速列车速度跟踪
肖龙,梁新荣,王雪奇,董超俊
(五邑大学 智能制造学部,广东 江门 529020)
技术的进步和经济的发展促使轨道列车速度不断提高,轨道线路里程持续增长.同时,先进技术不断提高了高速列车运行的性能并保障了高速列车运行的安全.近年来,列车自动驾驶(ATO)的研究倍受学者们的关注,研究方法也从传统的控制技术向先进的控制技术演化.对列车速度和位置的跟踪控制是ATO 的重要研究内容,其研究策略是通过建立适当的列车动态模型并采用合适的控制方法使列车沿期望的目标轨迹运行.
建立适当的列车动态模型是随后研究的基础,通过应用牛顿第二定律的动力学原理可以建立列车动态模型.然而,由于列车运行环境的复杂性以及运行过程的非线性,要得到一个准确的列车动态模型是困难的.文献[1]研究了列车传递函数模型,并用遗传PID 进行了仿真验证;文献[2]中列车运行控制模型采用传递函数模型,并研究了智能驾驶算法;文献[3]研究了列车单质点模型,它将列车视为一个刚性质点.从已有的文献来看,单质点模型应用较多[4],单质点模型的不足在于它没有考虑列车车厢之间的相互作用力,因而模型并不准确,建模精度有待提高.考虑列车的内力,文献[5]研究了列车多质点模型.多质点模型比单质点模型更为准确且更接近实际情况,多质点模型的缺点是其计算的复杂性,因此必须简化多质点模型,并同时保持多质点模型的准确性.基于此,本文研究了一种单位移多质点模型.
另一方面,出现了多种多样的列车自动驾驶算法,例如:PID 控制[6]、模糊控制[7]、模糊PID控制[8]、遗传算法[9]、蜂群算法[10]、广义预测控制[11]、模型预测控制[12]、滑模预测控制[13].虽然高速列车控制方法较多,但各种方法都有自身缺陷.常规PID 控制的缺点是参数调节繁琐,需要人工反复试凑;模糊控制和模糊PID 控制结果的好坏依赖于隶属度函数的选取和规则库的建立,与设计人员经验有关;遗传算法的不足之处是交叉率和变异率的选择会极大地影响解的品质,而且遗传算法容易陷入“早熟”;蜂群算法容易得到局部最优解而不是全局最优解,并且搜索时间较长;广义预测控制很少考虑在线辨识和滚动优化对系统稳定性和鲁棒性的影响,并且传统的广义预测控制计算量大、算法复杂;模型预测控制从本质上说是求解一个最优控制问题,其实现与模型有关;滑模预测控制不能完全消除抖振现象.并且上述大部分研究主要集中于列车传递函数模型和简单的列车单质点模型.
本文研究一种单位移多质点模型,并设计一种高速列车速度跟踪径向基函数(RBF)神经网络整定的PID 控制,最后提供数值仿真来证明所提出方案的有效性.
1 高速列车单位移多质点模型
下面在文献[5]多质点模型的基础上,阐述一种改进的高速列车多质点模型,并在本节结尾处分析比较这两种多质点模型.
考虑一辆列车,它由n 节车厢通过耦合器相连接,如图1 所示.
由牛顿第二定律得

图1 由n 节车厢相连的列车

其中,mi是第i 节车 厢的质 量;分别 是第i 节车 厢的位 移、速度 和加速 度; ui表示 第i 节车 厢的牵引力和制动力; fci是第i 节车厢经受的列车内力,它由耦合器产生; fri是第i 节车厢的阻力,其中首节车厢还有一个额外的阻力,它由空气阻力产生.
方程(1)能反映高速列车的动态特性,但计算量相当大.下面进行简化以得到单位移多质点模型:
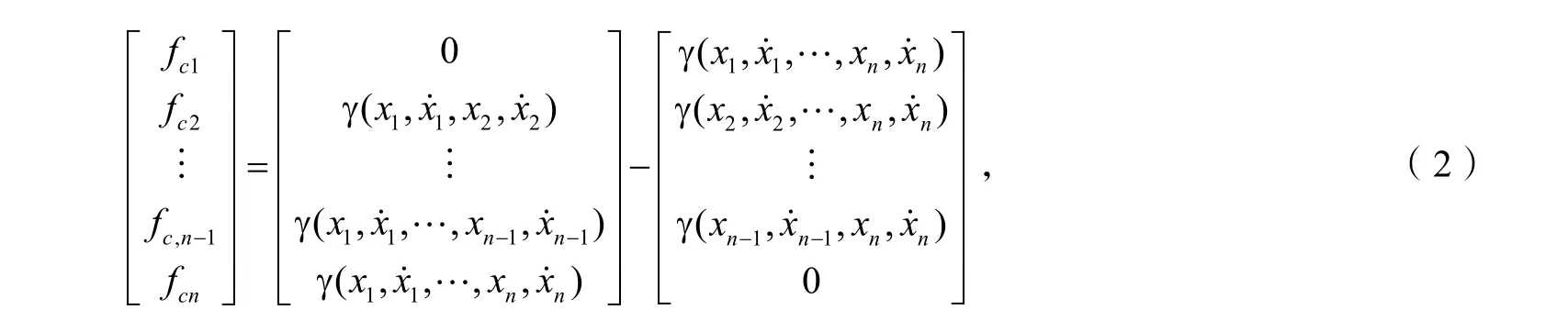
式(2)中右边第一项表示来自所有前面车厢的作用力,易知该向量的第1 个元为零;右边第二项表示来自所有后面车厢的作用力,易知该向量的最后1 个元为零.
两节车厢之间的连接可由 ixΔ 表示的弹性部分来描述,因此第i 节车厢和第 i-1 节车厢之间的距离可描述为:

其中K 为固定的数.相邻车厢之间的位移、速度和加速度可描述为:

其中 i=2,3,…,n.选择首节车厢为参考点,则首节车厢和第i 节车厢之间的距离、速度和加速度可描述为:

其中Km为固定长度.方程(1)可写为:

将式(5)中的加速度关系代入到式(6)得:

将式(7)的两边相加,便得到列车单位移多质点模型:

式(8)的单位移多质点模型已经考虑了车厢之间的作用力,该模型能更好地描述列车的动态行为,而且计算过程并不复杂.
值得一提的是:式(7)两边相加后,所有的 γ ()· 项相互抵消了,这点也可以从如下的分析中得到.考虑车厢之间的相互作用力,式(6)可写为:

将式(5)中的加速度关系代入到式(9)得:

将式(10)两边相加,并利用车厢之间相互作用力 和反作用力之间的关系同样可以得到式(8)的列车单位移多质点模型.
接下来对文献[5]的多质点模型和本文的多质点模型进行分析比较,这两种多质点模型都是根据牛顿第二定律建立车厢加速度与车厢受力之间的关系式.文献[5]研究100 至200 节车厢的重载长列车,车厢的受力包括牵引力及制动力、弹簧力、阻尼力、滚动阻力、空气阻力(仅首节车厢考虑)、坡道阻力和弯道阻力.本文研究8 至16 节车厢的高速列车,车厢受力包括牵引力及制动力、车厢耦合器产生的列车内力和车厢的阻力.其中本文车厢耦合器产生的列车内力包括了文献[5]的弹簧力和阻尼力.本文车厢的阻力包括了滚动阻力、空气阻力、坡道阻力和弯道阻力.在本文后面的仿真中把滚动阻力和空气阻力合并为基本阻力 (a+bv +cv2),并把坡道阻力和弯道阻力计入附加阻力中.
考虑到高速列车车厢数较少(一般为8 节或16 节车厢),车厢之间耦合器弹性元件的伸缩距离一般不超过20 cm,本文对多质点模型进行了简化,在简化时,选择首节车厢作为参考点,建立了其余车厢与首节车厢之间的距离、速度和加速度关系式.在最后得到的多质点模型式(8)中,等式左边只有首节车厢的位移1x (对应的加速度为),因此本文的模型称为单位移多质点模型.
最后再进一步说明本文的多质点模型与文献[5]中多质点模型的差别:文献[5]的模型是多位移多质点模型,其运动方程的左边各式包含对应的位移分别为 x1,…,xi,…,xn,即多位移模型.本文的模型是单位移多质点模型,式(10)中左边各式包含(注意下标),对应的位移只有1x ,即简化为单位移模型.此外,文献[5]的模型其运动方程的右边相加后车厢之间的相互作用力一般不会抵消.本文的模型其运动方程式(10)的右边相加后会抵消一部分车厢之间的相互作用力,但车厢之间相对加速度引起的作用力不会抵消.本文模型的优点是计算过程相对简单,而文献[5]的模型计算过程比较复杂.
2 高速列车速度跟踪RBF-PID 控制
2.1 RBF 网络结构与被控对象雅可比辨识算法
RBF 神经网络是一个包含输入层、隐含层和输出层的前馈网络[14],本文采用多输入单输出神经网络,网络输入层有n 个神经元,隐含层有m 个神经元,输出层有1 个神经元.X=[x1,x2,…,xn]T为输入向量,ym为输出量,为隐含层向量,其中

RBF 网络隐含层到输出层的权向量为

RBF 网络输出my 为

被控对象辨识指标定义为

其中 yout(k) 为被控对象的输出.从隐含层到输出层的权值更新算法为:

其中η 表示学习率,α 和β 表示动量常数.式(11)中 bj和 cji的迭代过程为:

被控对象雅可比辨识算法为:
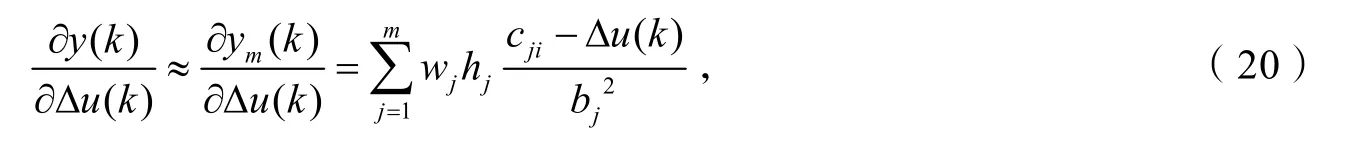
其中Δu (k)为被控对象的输入增量.
2.2 RBF 网络整定的PID 控制
被控对象RBF 网络整定的PID 控制如图2 所示.
从图2 可以看出,误差信号 error(k)=rin(k)-yout(k),PID 输入为


图2 RBF 网络整定的PID 控制
被控对象的控制输入为 u (k)=u (k-1) +Δu (k),其中 Δu (k)计算式[15]为

RBF 网络整定的性能指标定义为

kp,ki,kd的增量 算法为

2.3 高速列车速度跟踪控制器
对于任意给定的期望速度,与速度—距离曲线相对应,列车应能在可接受的误差范围内跟踪它,以保障列车的运行安全.图3 是设计的高速列车速度跟踪控制器,采用的控制方法是RBF 网络整定的PID 控制,被控对象是高速列车动态模型,这里采用式(8)的单位移多质点模型.图3 中dv 为列车期望速度,对应图2 中的系统输入 rin,图3 中av 为列车实际输出速度,对应图2 中的系统输出 yout,图3 中RBF 整定PID 的控制算法采用2.2 节的算法,而2.2 节的被控对象雅可比辨识结果采用2.1 节的辨识算法.
下面具体说明RBF 神经网络利用样本数据的训练过程.
本文的样本数据为列车期望速度 vd,在图2 中,rin=vd,yout=va,其中 va为列车实际速度.对于给定的样本数据 rin,被控对象(即高速列车动态模型)的输出为 yout,RBF 网络产生的输出为 ym,根据 yout与 ym的差值用公式(15)、(16)和(18)更新 wj(k),Δbj和Δcji,然后用公式(17)和(19)得到 bj和 cji,将它们代入到公式(20)中可得到被控对象雅可比辨识结果,再将代入到公式(24~26)中更新 kp,ki和 kd,从而使PID 控制器产生新的控制量u,该控制量对应的牵引力和制动力使列车产生新的实际速度av (即 yout).
图3 是一个非线性反馈闭环控制系统,系统的输入是列车期望速度,系统的输出是列车实际速度,牵引力和制动力是控制变量,通过选择合适的牵引力和制动力使列车实际速度跟踪列车期望速度.与开环控制相比,这种非线性反馈闭环控制能够抑制列车建模误差,抑制系统干扰和噪声,系统具有鲁棒性强、响应速度快、跟踪误差小等优点.
3 仿真结果
考虑由4 节拖车和4 节动车组成的一辆高速列车,列车重量为840 t;基本阻力公式 a+bv +cv2中的参数分别是a=0.53,b=0.003 9,c=0.000 114; 列 车 最 大 速 度 为400 km/h,ATP 限速是405 km/h.对图3 所示的速度跟踪控制器进行仿真,图3 中的单位移多质点模型考虑了基本阻力、附加阻力和车间力(即:车厢之间的相互作用力).根据2.1 节和2.2 节的控制算法编写仿真程序.期望速度样本数据和列车参数数据来源于北京交通大学,仿真结果如图4、图5 和图6 所示.从图4 和图5 可以看出,实际速度可以很好地跟踪期望速度,且实际距离可以很好地跟踪期望距离.由图6 可知,在整个过程中,速度跟踪误差控制在 ±8 km/h 的范围内.
本文的仿真使用一台普通的Intel CORE i3、内存为4 GB 的计算机,RBF 神经网络对500 个样本数据的训练时间仅为0.1 s,该RBF 神经网络响应速度快,完全可以在线工作.
为了进一步说明RBF 神经网络PID 控制的控制效果,在仿真参数完全相同的情况下,我们还采用49 条规则的模糊控制和PID 控制进行仿真对比.结果表明,3 种方法都能实现速度跟踪和距离跟踪,但跟踪效果和跟踪性能有一定的差别.表1 比较了3 种方法的控制性能.可以看出,RBF 神经网络PID 控制具有最好的速度跟踪性能.

图3 高速列车速度跟踪控制器

图4 速度跟踪
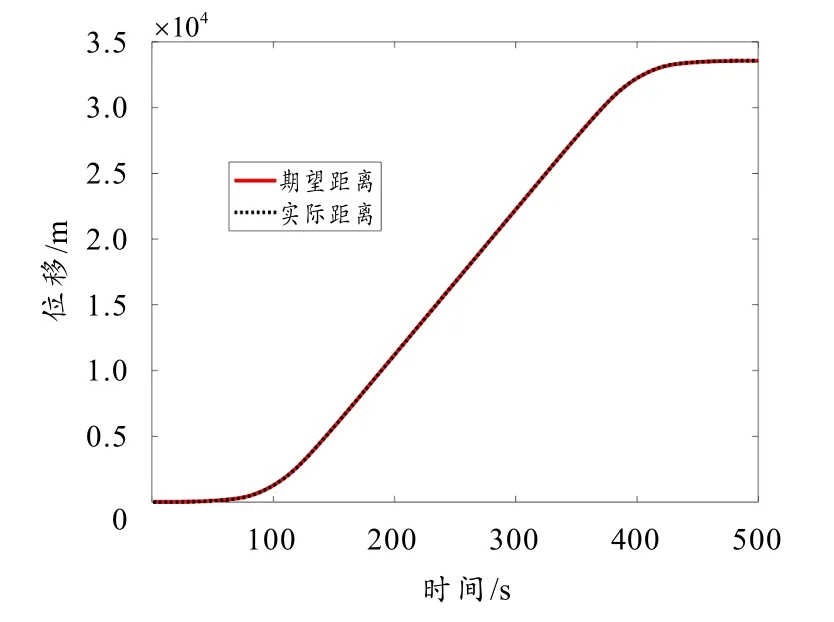
图5 距离跟踪

图6 速度跟踪误差

表1 3 种方法性能比较
4 结论
本文提出一种高速列车速度跟踪控制的新方法.该方法对高速列车多质点模型进行改进,构建了只考虑首节车厢位移的多质点模型,基于此模型并结合非线性反馈技术设计了速度跟踪RBF 神经网络PID 闭环控制系统,闭环控制提高了控制系统的性能.实验中分别采用49 条规则的模糊控制、常规PID 控制以及本文提出的方法对北京交通大学提供的样本数据进行仿真对比.通过对比实验可知,本文方法具有最好的跟踪性能,速度跟踪误差很小,并且RBF 神经网络训练时间很短,系统响应速度快,完全能够满足列车安全、正点运行的需求.
值得注意的是,本文从机理建模角度,通过分析列车受力来得到列车动力学模型,但没有充分利用列车实际运行过程中产生的海量数据.下一步要用数据驱动建模并用人工智能+大数据的方法研究列车运行控制.

