关于四元数指数函数的注记
常振虎,唐哲,曹文胜
(五邑大学 数学与计算科学学院,广东 江门 529020)
众所周知,指数函数ex有幂级数展开式,且其收敛半径为无穷大,即有

将此级数扩展到复数域,并令x=i,θ θ∈R,便得到著名的欧拉公式[1]:
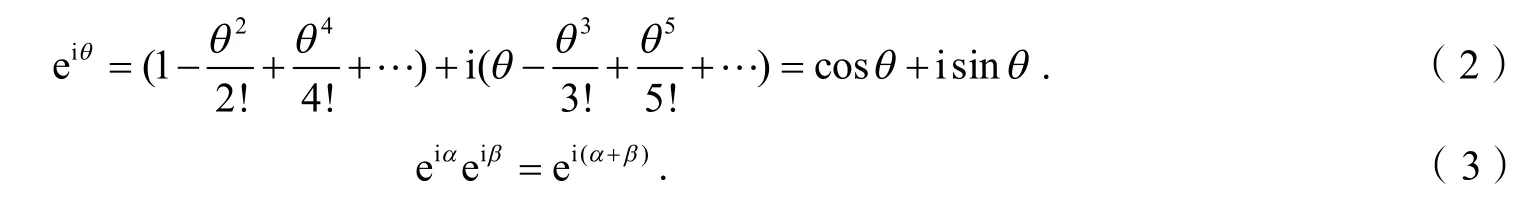
四元数是Hamilton 于1843 年发现的数学概念.记R 和C 分别表示实数域和复数域,则四元数可表示为
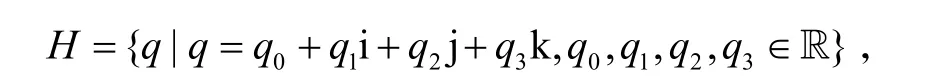
其中,i,j,k 满足如下乘法表:


1 相关定义及引理
定义1对任意四元数q,我们定义

显然,eq也是一个四元数,且当q 是实数或复数时,就是我们常见的实数域或复数域上的指数函数.
要使式(5)有意义,需要判定式(5)右边是否为收敛的级数,而这是显然的.因为我们知道当q∈H C时,存在p≠ 0,使得 pqp-1=Re(q)+|Im(q)|i=qc∈C[4],而进而

由复变函数关于复数幂函数的知识(详见参考文献[1]第161 页例4.6),得到式(5)的左边对任意四元数是收敛的,因而定义1 是有意义的.
定义2如果四元数u 满足Re(u)=0,|Im(u)|=1 ,我们定义u 为四元数的一个虚数单位,简称虚数单位.如:等都是虚数单位.
在 R3空间中,x=(x1,x2,x3),y=(y1,y2,y3)的内积为我们可以把四元数q 的虚部 Im(q)=q1i+q2j+q3k 视作三维向量 (q1,q2,q3),则我们有
引理1设 u=u1i+u2j +u3k ,v=v1i+v2j+v3k,则:uv=-u·v+u×v.
证明由四元数计算规则知:


2 四元数上的欧拉公式
定理1设u 是四元数虚数单位,θ∈R,则有

证明因为u 为虚数单位,所以u3=-u,u4=1,…,将q=uθ代入式(5),得:
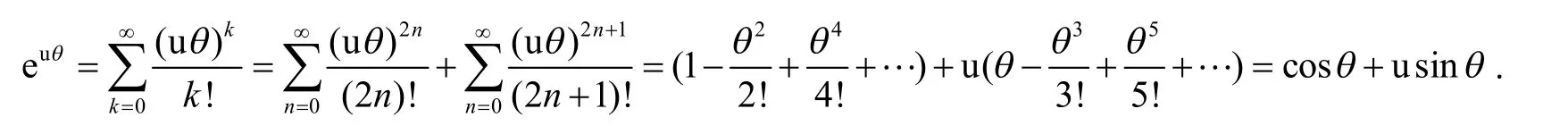
我们把上面的公式称为四元数上的欧拉公式.
定理2设 q=q0+qv,其中 q0=Re(q),qv=Im(q),则有
证明对四元数 q=q0+qv,其中 q0是实部,qv是虚部,由式(5)知:

由定理1 知
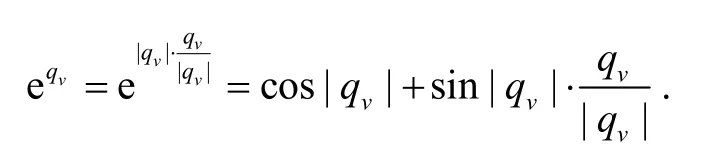
推论1设u 是单位虚数,则:
证明利用 euθ=cosθ+u sin θ,e-uθ=cosθ-usin θ,两式相加或相减立即得出上面的结论.
3 四元数的辐角和对数函数
设 q=q0+q1i+q2j+q3k=q0+qv≠ 0.我们把四元数看作四维空间中的一个点,则以原点为起点,q 为终点的向量与四元数q 一一对应,此向量与x 轴一起张成一个二维平面.这个平面的基为x=(1,0,0,0)和 (0,q1,q2,q3)这两个向量.我们可视此平面类似于复平面,则在此类复平面上,将正实轴和之间夹角的弧度数θ 定义为q 的辐角,记作arg(q)=θ.在这里有当然,辐角有无穷多个,我们把满足条件 0≤θ0≤π的辐角称为arg(q)的主值,记为那么很显然 arg(z)=θ0+2kπ,其中k 为任意整数.在这里需要说明的是,在传统的复平面上辐角的主值是 0≤θ0<2π,但放在四元数的情形下时,考虑到 euθ=e(-u)(-θ),我们取主值为0≤θ≤π.下面讨论四元数的指数表示.
设q=q0+qv=reuθ=r (cosθ+usin θ),则有 q0=r cos θ,qv=ru sin θ.故有即

在指数表示下,两个四元数相等是指模长相等,辐角也相等.与复变函数中相关理论类似,在四元数体上,定义对数函数与指数函数互为反函数,则满足方程eω=z (z ≠ 0)的函数 ω=f (z)为四元数变量z 的对数函数.
令四元数 ω=ω0+ωv,其中ω0为实部,ωv=Im(ω),z=r euθ.则
由四元数相等及关于辐角的说明,有
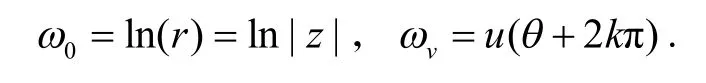
所以对数函数 ω=f (z)可记作

其中k 为任意整数,ln|z|∈R 为实函数中的对数函数.
设u 是某 一四元 数虚数 单位,则有 euθeuβ=(cosθ+sin θu)·(cos β+ sin βu)=eu(θ+β).由于 四元数 的虚数单 位众多,所以 上式 eiθeiβ=ei(θ+β)是形 式上的 推广.从四 元数模 的性质 我们知 道,euθ与 evβ的乘 积仍是模为单位1 的四元数,可以表示为 ewα的形式,下面讨论w,α 与u,v,θ,β 的关系.
定 理3设u,v 为 四元 数虚 数单 位,则 euθevβ=ewα,其中 α=arccos [cos θcos β-sin θsin β(u·v)],
证明由定理1 知

又因为 ewα=cos α+w sin α,由四元数相等知
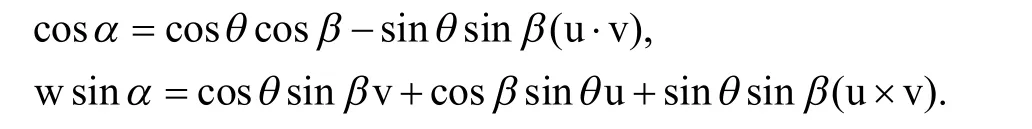
故可得

例1已 知 a1,a2,b1,b2,α,β∈R,设 I=cos a1sin b1i +cos a1cos b1j +sin a1k ,J=cos a2sin b2i +cos a2cos b2j +sin a2k,则由定理3,我们可得出eKγ=eIαeJβ,其中


