基于等效夹杂法的界面热应力分析

黄云海，张炯，刘卫东

（1.五邑大学 土木建筑学院，广东 江门 529020；2.河海大学 机械学院，江苏 南京 210098）

颗粒增强复合材料因其优异的力学和热学性能，被广泛应用在航空航天等领域.这些材料经常处于温度急剧变化的环境中，由此引起的应力集中是导致颗粒增强复合材料破坏的一个主要原因.所以在研究复合材料破坏的问题中，确定含椭圆夹杂平面的热弹性场具有重要意义.

针对以上问题，很多学者进行了大量的研究，Lekakis[1]采用复势函数、共形映射和解析延拓方法，研究了在无限处的均匀热流作用下椭圆夹杂物的热弹性问题.Shen[2]基于复变函数方法导出了用无穷级数表示的热弹性场.戴明[3]借助保角变换法、Faber 级数和Fourier 级数等工具，求解了含多个夹杂椭圆平面的热弹性场.Lee[4]采用等效夹杂法并结合三维椭球的Eshebly 内部张量，计算了在无限大空间内由于椭球夹杂温度变化引起的热应力.

但是，在用上述共形映射、复变函数和级数等方法求解该问题时，计算过程较为复杂.为了简化计算过程和提高计算效率，本文在文献[4]的基础上采用等效夹杂法并结合二维的Eshelby 内部张量和外部张量，以期更简便和精确地求解含单个椭圆夹杂平面在均匀温度变化下的热弹性场.

1 等效夹杂法

假设在弹性常数为的某无限大平面内存在一个弹性常量为的椭圆夹杂，如图1 所示，椭圆夹杂的长轴与x轴的夹角为θ；椭圆夹杂的长短轴之比Γ=a/b；夹杂物和基体之间的线膨胀系数差值为Δα；夹杂物和基体的剪切模量比为；整个平面温度变化为ΔT.

将图1 的椭圆夹杂转化为图2 所示的问题.在图2 中，将椭圆夹杂转化为位置和形状不变但弹性常量变为的夹杂；同时在夹杂内部会产生本征应变（）[5]，由于本征应变的产生，会在夹杂内部和外部产生扰动应变（）：

其中Sijkl为内部张量[6]；Gijkl为外部张量[7-8].

图1 含椭圆夹杂的无限大平面受到均匀温度变化示意图

图2 等效夹杂法示意图

根据图1 和图2 所示问题，可在夹杂中心建立应力平衡方程：

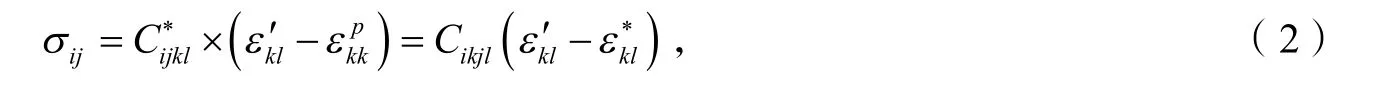
其中[4]是由温度变化引起的均匀应变

根据上述的等效夹杂法和Eshelby 内部张量，若夹杂椭圆内部的本征应变为，通过式（1）可以得到椭圆夹杂的内部应变，根据式（2）可以求得夹杂的内部应力场为：

同理可根据上述的Eshelby 外部张量，若夹杂的椭圆内部受到均匀的本征应变，结合式（1）可以求得椭圆夹杂的外部应变，然后根据式（2）可以求得夹杂外部的应力场为：

这样便可根据Eshelby 的内部和外部张量求解出温度变化下弹性体的应力应变场.

2 算例对比验证

将上述方法利用FORTRAN 编程实现，并对相应的算例进行分析（典型算例：无限平面含单个倾斜椭圆夹杂），然后将本文方法的计算结果与有限元软件的计算结果进行比较，以验证其有效性.所有计算均在1.8 GHz 的i5 CPU 电脑上进行.本文算例均假设为平面应变问题.

在含单个椭圆夹杂的无限大平面内均匀升温1 C° ，基体和夹杂的剪切模量分别为2.6 GPa 和13.0 GPa，泊松比为0.3；其余参数固定为：a=2.0，b=1.0 ，θ=30°，0.01αΔ=；然后分别用本文方法和有限元方法对含单个椭圆夹杂平面的热弹性场进行计算.

由图3～5 可知，采用本文方法所得的计算结果和有限元的计算结果吻合较好，验证了本文方法的有效性和精确性.在计算图3 所示的s22 应力（y轴方向应力）分布时，本文方法用时为10.4 s，而有限元法用时为72.2 s，表明本文方法具有更高的计算效率.此外，采用有限元计算时，要对模型进行划分网格，然后同时求解；而本文方法在计算各个点的应力时是独立的，与其余点无直接联系，可以仅对局部进行求解，计算效率大大提高.

图3 s22 应力分布（θ=30°，K=5.0）

图4 s12 应力分布（θ=30°，K=5.0）

图5 Mises 应力分布（θ=30°，K=5.0）

3 材料参数和几何参数对界面应力的影响

由于夹杂物和基体之间的线膨胀系数不同，在温度变化时会产生热失配，由此引起的界面应力集中是导致材料破坏的一个重要原因，因此研究椭圆夹杂的材料参数和几何参数对界面热应力的影响有着重要的现实意义.

以下算例均采用本文方法对含单个椭圆夹杂平面的热弹性场进行计算，基体和夹杂物的泊松比均为v=0.3，并分别求出界面的径向应力差值（Δσr），环向应力差值（Δσθ），剪应力差值（Δσrθ）.

3.1 材料参数对界面应力的影响

图6 在K变化下的界面径向应力差值

由图6～8 可知，3 个界面应力差值的增幅随着K的增大而逐渐减缓；Δσr和Δσrθ随着K的增大其最大值逐渐向45°的位置靠近，而 Δσθ的最值在K＜1时出现在长轴端点，在K≥1出现在短轴端点.当K=10.0时，随着夹杂物剪切模量的增长其界面应力差值缓慢增加，在实际工程允许的情况下可以尽量选择与基体剪切模量差值大的夹杂.

图7 在K变化下的界面环向应力差值

图8 在K变化下的界面剪应力差值

3.2 几何参数对界面应力的影响

算例1：基体和夹杂的剪切模量分别为2.6 GPa和0.52 GPa，固定 ΔT=1°C,b=1.0,Δα=0.01.研究a分别取1.1，2.0，5.0 和10.0 时，界面应力差值的变化情况.

由图9～11 可知，Δσr随着Γ的增加其最大值逐渐向长轴端点靠近；Δσθ的最大值随Γ增加而增加且最大值出现在长轴端点，短轴端点处的 Δσθ随Γ增加其增幅逐渐减缓；Δσrθ的最大值随Γ增加其增幅减缓且最大值出现的位置逐渐向长轴端点靠近.

图9 在Γ变化下界面的径向应力差值

图10 在Γ变化下界面的环向应力差值

图11 在Γ变化下界面的剪应力差值

算例2：基体和夹杂的剪切模量分别为2.6 GPa 和13.0 GPa，固定 ΔT=1°C,b=1.0,Δα=0.01.研究a分别取1.1,2.0,5.0 和10.0 时，界面应力差值的变化情况.

由图12～14 可知，3 个界面应力差值的峰值随着Γ的增加而增加； Δσr随着Γ的增加其峰值出现的位置逐渐向长轴端点靠近； Δσθ和Δσrθ随着Γ的增加其增幅先增加然后减缓.

由算例1 和2 可以看出，硬夹杂界面应对力夹杂物离心率较为敏感，为了减少界面处的应力集中，可以选择几何参数与圆形较为接近的夹杂.

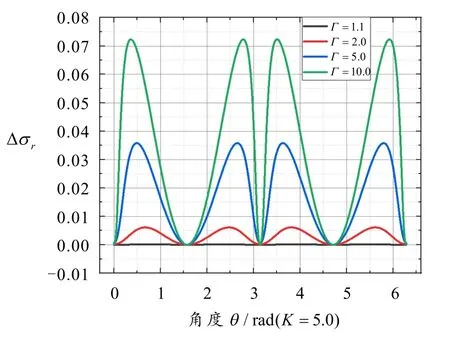
图12 在Γ变化下界面的径向应力差值

图13 在Γ变化下界面的环向应力差值

4 结论

本文基于等效夹杂法并结合Eshelby 内部张量和外部张量，推导了无限大平面内含单个椭圆夹杂在温度均匀变化下热弹性场的计算公式，并通过典型算例验证了本文方法的有效性和准确性，由于本文算法可以仅对局部进行计算，计算效率大大提高.最后，通过多个算例分析了材料参数和几何参数对热弹性场的影响，结果可为复合材料的工程应用提供理论依据.但是，本文算法只能计算无限平面下的热弹性场，无法计算有限平面内的问题，所以对材料尺寸的要求比较高.针对该问题，可以通过设置边界条件并与错位分布法结合来实现有限平面内热弹性场的计算，今后还可以进一步扩展到三维夹杂的热弹性问题.