龙门加工中心横梁材料特性参数确定的方法研究

刘光辉，周俊荣，胡晨星

（五邑大学 智能制造学部，广东 江门 529000）

模态分析是振动理论的一个重要分支，是研究结构动力特性的一种近代方法，是系统识别方法在工程振动领域中的应用[1].模态分析的目的是识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预测以及结构动力特性的优化设计提供依据.按照模态分析的手段和方法，模态分析分为试验模态分析和计算模态分析.试验模态分析是通过对模态测试采集到的数据进行参数识别获得模态参数；计算模态分析是通过有限元计算获得模态参数.试验模态分析可以验证有限元模型，提高计算模态分析的准确性.

近年来随着计算机技术与数值分析方法的不断发展，有限元分析在模态分析领域得到了广泛的应用.季彬彬、张森和杨玉萍等人以GMF3022龙门加工中心横梁为研究对象，对横梁的模态及谐响应特性进行了研究，得到了横梁的固有频率、振型和幅频响应曲线[2].曹建华和杨铁牛以双铣刀螺杆专用数控铣床为研究对象，利用LABVIEW软件和NI数据采集卡等采集机床振动信号，在MATLAB软件中采用复模态指示函数法对机床进行试验模态分析，得出其固有频率和相关振型[3].美国学者E.Kushnir和Hardinge Inc等基于能量平衡原理和有限元法，分析得到了影响机床结构动态特性的主要振型，并对机床结构进行了优化设计[4].然而，由于有限元模型与实际结构会有出入，从而可能导致计算结果存在偏差.

横梁是龙门加工中心的重要支撑部件，其动态特性是影响加工中心整机动态特性的关键因素.通过对横梁进行模态分析，建立准确的横梁有限元分析模型，是龙门加工中心整机振动特性分析和优化设计的重要前提.本文以某公司的G-V2330R2龙门加工中心横梁为研究对象，应用模态分析软件ME、Scope对试验数据进行模态参数识别，根据模态置信准则对得到的模态结果进行验证.由于材料特性参数对计算模态分析结果有明显影响，本文利用模态试验与数值模拟结合的手段，基于多目标自适应混沌粒子群优化算法进行MATLAB和ANSYS Workbench的联合仿真，得到零件材料的属性参数，以获得可靠的有限元模型.

1 龙门加工中心横梁试验模态分析

1.1 横梁模态试验

本文采用FRF频响函数法对G-V2330R2龙门加工中心横梁进行模态试验分析.FRF频响函数法是将振动激励和响应的时域信号数据经快速傅里叶变换（FFT）转化为频域数据，对所建立的机械结构频响函数的数学模型进行曲线拟合，从频响函数求出所测系统模态参数.由于龙门加工中心横梁具有体积和质量大，且结构较为复杂等特点，选用单点激励多点采集的模态试验方案[6-7].

试验采用台湾基太克国际股份有限公司的产品ImpaqTMElite频谱分析仪采集数据，使用ME、Scope软件对采集的数据进行处理分析，三向传感器则用于产生反馈点信号.为避免敲击对试验对象本身的影响，使用了橡胶材质的敲击锤作为模态试验的激励.

由于试验对象具有体积大和重量大等特点，在选取反馈点连成横梁轮廓时省略了横梁细微特征.同时，对贯穿大孔以及易产生应力集中的结构，在设置激励反馈点时进行了着重考虑.ME、Scope软件建立的横梁传感器布置点和基本轮廓如图1所示.

图1 试验中横梁传感器布点与基本轮廓图

反馈点信号是敲击锤激励时产生的，因此将敲击锤连接于一号通道.三向传感器测试可接收3个方向的反馈数据，将传感器上X向、Y向和Z向分别对应频谱分析仪的2号通道、3号通道和4号通道.在测试时对横梁上的坐标轴与传感器上的坐标轴进行了校对，确保测试所得数据与ME、Scope软件的模型坐标轴相对应，避免数据错误.基于以上模态试验方法进行了G-V2330R2龙门加工中心横梁的模态试验，试验现场如图2所示.

图2 G-V2330R2龙门加工中心横梁模态试验现场

1.2 试验结果与分析

本次试验成功采集到了234组有效数据，702个有效激励反馈信号，并使用ME、Scope软件进行了横梁的模态分析，得到了横梁的前六阶模态振型和频率（限于篇幅仅展示前2阶振型），如图3所示.

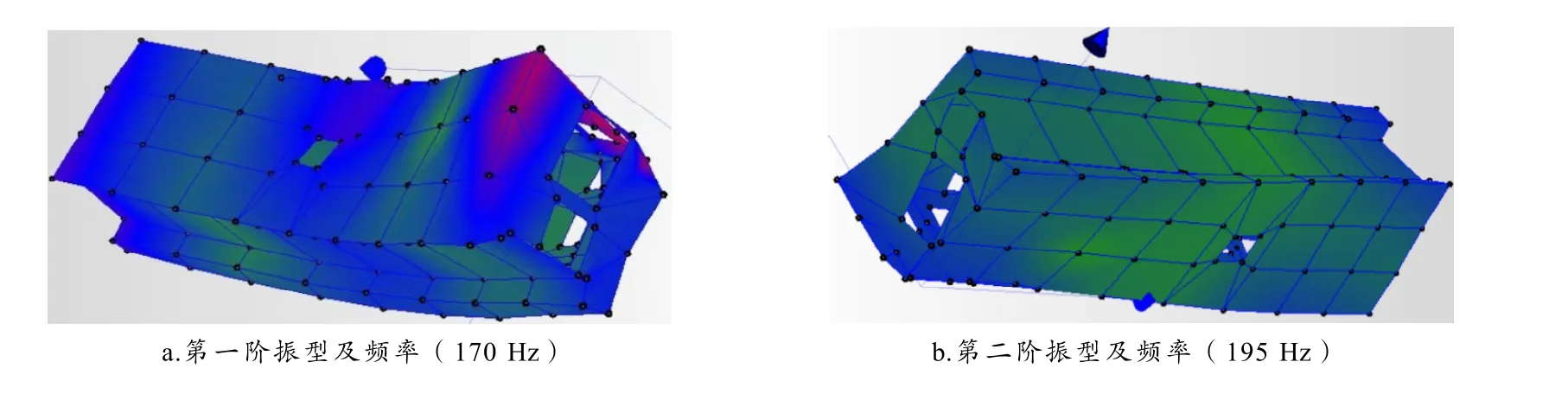
图3 横梁模态试验所得前二阶振型及固有频率

分析模态试验所得的各阶模态振型可知：横梁第一阶模态振型为YZ平面内绕X轴的摆动，固有频率为170 Hz；横梁第二阶模态振型为绕Z轴的扭转，固有频率为195 Hz；横梁第三阶模态为“点头”模态，固有频率为212 Hz；横梁第四阶模态为中间部位绕Z轴扭转，固有频率为287 Hz；横梁第五阶模态为两端沿Y向的摆动，固有频率为311 Hz；横梁第六阶模态为Z向端绕Z轴的扭转，固有频率为343 Hz.

1.3 模态验证

通过模态验证可以对试验模态分析识别的参数结果精度进行检验.模态置信准则是常见的模态验证方法（Modal Assurance Criterion，MAC），MAC是振型向量之间的点积，可用其评价两个振型向量在集合上的相关性和表示模态分析结果的可信度.两模态振型向量φr与φs的MAC值定义[8]为：

若MAC 值接近于0，则向量φr与φs线性独立；若MAC值近似于1，则二者线性相关.龙门加工中心横梁的前六阶试验模态参数的MAC矩阵直方图如图4所示.模态验证结果显示对角线上同向量间的MAC值为1，其余各模态向量间的MAC值最大为0.095，说明各模态向量线性独立，试验得到的模态参数可信度高.

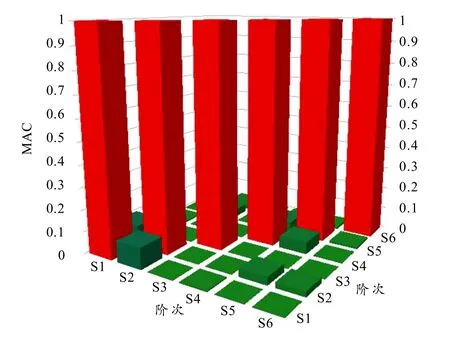
图4 横梁模态试验MAC矩阵直方图

2 计算模态分析

计算模态分析是采用有限元方法获得模态参数，对有限元结果的评估方法有表象评估法、数值评估法和物理样机法3种方法.本文基于多目标混沌粒子群遗传算法，采用物理样机法进行评估，对比有限元结果和试验结果，并以试验结果为依据修正有限元模型，获得精确的材料属性参数.

2.1 多目标自适应混沌粒子群算法

粒子群优化算法具有概念简明、收敛速度快、易于编程实现等特点，在复杂组合优化问题方面得到了广泛的应用.粒子群优化算法速度和位置更新公式如下：

其中，1≤i≤N，1≤d≤D；i为粒子标号；N为示种群规模；d为决策变量维度标号；D为决策变量总维度；x为粒子位置；v为速度；t为进化代数；pb为粒子个体历史最优位置；gb为粒子全局历史最优位置；ω＞ 0为惯性因子；c1为个体加速因子；c2为全局加速因子；r1和r2表示［0,1］ 间的随机数.

在粒子群算法运算初期，为提高算法运行效率，加快种群收敛速度，应适当减小种群变异规模.算法运行后期，应增大变异规模，使种群跳出局部最优，以防止种群收敛速度慢，甚至陷入局部最优，导致算法停滞.在基于外部存档的自适应变异策略中采用了式（4）的方式对变异规模进行调整.

其中，Q(t)为第t代外部存档变异规模，且需满足0＜Q(t)≤z，z为当前外部存档规模；t=1,2,3时，Q(t)=z； ΔGD*为相邻两代解集的差值[9].

2.2 目标函数与约束条件

材料的密度、弹性模量和泊松比是影响各阶模态振型和固有频率的关键因素，因此设计变量作如下定义，

其中，ρ为材料的密度，kg/m3；E为材料的弹性模量，GPa；μ为材料的泊松比.

目标函数为龙门加工中心横梁的前六阶模态固有频率的仿真值相对试验值的误差率.即

其中，gi(X)为第i阶模态固有频率的仿真值相对试验值的误差率最小值；fis为第i阶模态固有频率仿真值，Hz；fit为第i阶模态固有频率试验值，Hz.

根据横梁材料灰铸铁HT250的密度、弹性模量和泊松比的分布范围，可将约束条件定义为

2.3 横梁有限元模型建立及网格划分

采用UG对横梁进行三维建模，导入ANSYS Workbench进行无约束的自由模态分析.在进行模态分析之前需对模型进行适当的简化，去掉螺纹孔及小圆角、倒角等.因横梁由灰铸铁HT250焊接而成，各结合面接触类型设置为Bonded.同时，采用六面体高阶单元对横梁进行全局和局部网格划分，得到了如图5所示的有限元模型，其中有限元模型单元数为244 520，节点数为394 584.

2.4 确定材料特性参数

图5 横梁有限元分析模型

材料特性参数密度、弹性模量和泊松比会直接影响结构模态分析结果的可靠性.为在不破坏零件的前提下获得横梁可靠的材料参数，利用有限元分析与模态试验相结合的方法，对其采用多目标自适应混沌粒子群优化算法.以龙门加工中心横梁的前六阶模态固有频率的仿真值相对试验值的误差率为目标函数，以横梁材料灰铸铁HT250的密度、弹性模量和泊松比的分布范围为约束条件.采用MATLAB为主控程序，编制多目标自适应混沌粒子群优化算法，将基于ANSYS软件平台得到的横梁前六阶模态固有频率作为输入和约束返回给MATLAB优化程序，以此确定固有频率误差率最优时所对应的横梁材料参数.设置算法种群规模为100，算法迭代次数设为100，外部存档最大规模为100，收敛稳定性百分比为2%，由此得到了非劣最优解集在目标空间中的分布，前3个Pareto最优解集见表1.

表1 横梁材料参数优化结果表

由表1可知：横梁材料参数的多目标优化问题的各子目标是相互冲突的，即前六阶模态固有频率的仿真值相对试验值的误差率不可能同时达到最优解.由于模态阶数越低，频率对结构固有特性的影响越大，而解集1前三阶频率相对误差较小，因此选用解集1作为横梁的材料特性参数，即横梁材料密度ρ=7 293 kg/m3，弹性模量E=110.3 GPa ，泊松比μ=0.235.

2.5 模态仿真结果与试验对比分析

利用ANSYS Workbench默认求解器计算横梁自由边界条件下的前六阶固有频率和振型（限于篇幅仅展示前2阶振型），结果如图6所示.结果表明：计算模态分析与试验模态分析模态频率偏差较小，且振型一致.其中，横梁一阶固有频率仿真值为175 Hz，与试验值的相对误差率为3.1%；二阶固有频率仿真值为206.76 Hz，与试验值得相对误差率为6%；三阶固有频率仿真值为218.78 Hz，与试验值得相对误差率为3.2%；四阶固有频率仿真值为281.26 Hz，与试验值得相对误差率为8%；五阶固有频率仿真值为315.35 Hz，与试验值得相对误差率为1.4%；六阶固有频率仿真值为364.27 Hz，与试验值得相对误差率为6.2%.另外发现，低阶固有频率偏差较小，高阶固有频率偏差较大.由于模态分析的结构模型采用的是线性数学模型，忽略了一些实际结构中的非线性因素.此外，模型离散化误差和模型简化后与实际结构的偏差皆是计算模态与试验模态存在误差的主要因素.

图6 横梁仿真分析所得前二阶振型及固有频率

3 结束语

本文以某公司的G-V2330R2龙门加工中心为研究对象，对横梁结构进行了试验模态分析，识别了结构的模态参数，采用数值模拟与试验结合，基于多目标混沌粒子群优化算法确定了结构较可靠的材料特性参数，获得了可靠的有限元模型，得到以下结论：

1）计算得到的振型与试验识别得到的振型一致，再次验证了试验模态分析结果的可靠性.采用优化算法确定材料特性参数时，计算得到的振型没有差别，说明结构的参数特性对振型没有关键的影响.虽然不能通过预试验获得试验关心的频带范围，但可以通过计算模态分析得到结构的振型，为试验提供有效布置参考点和传感器位置的信息，从而避免模态的遗漏.

2）试验模态分析与计算模态分析得到的低阶固有频率偏差较小，而在高频偏差较大.因为阶次越高振型越复杂，而建模与实际结构的细节差异导致高阶结果产生较大偏差.

3）通过试验模态分析、计算模态分析和粒子群遗传算法优化相结合的方法获得了横梁准确的材料特性参数，为后续龙门加工中心整机的动态特性分析和结构优化提供了可靠的有限元模型.

4）相对传统的正交试验法，本文采用的多目标自适应混沌粒子群优化算法计算效率更高，得到的最优材料特性参数组合更精确.为进一步得到更精确的材料特性参数，后续可以通过对比多种优化算法的计算结果，采用更有效的优化算法实现.