资本深化、要素收入份额与全要素生产率——基于有偏技术进步的视角

余东华 陈汝影

一、引言

改革开放以来，中国经济保持了长期高速增长，创造了全球经济增长史上的“中国奇迹”。近年来，受到国际金融危机和国内经济矛盾的双重影响，中国经济结构调整步伐加快，经济增速逐渐放缓，经济发展进入新常态。2019年中国人均GDP已超过一万美元，按照世界银行制定的标准，中国正处于由中等收入向中高等收入跨越的关键时期。因此，对于中国这样的发展中大国，如何根据要素禀赋结构变动规律，选择适宜的技术进步路径，提升要素生产效率，推动由粗放式要素投入数量增长转变为集约式要素产出效率增长，实现经济高质量发展，是非常值得关注的问题。经济实践表明，持续的资本深化是中国改革开放后要素禀赋结构变动的具体表现，受到国民经济水平、宏观经济政策以及人口结构变动的影响，中国的资本深化速度呈现出明显的阶段性特征。

在上述背景下，研究要素禀赋结构的变动对经济发展质量的影响机制具有重要的现实意义。然而，学术界在对全要素生产率进行研究时，一般是基于中性技术进步的假定条件，无法将要素禀赋结构变动纳入全要素生产率的分析框架。近年来，越来越多的研究表明，无论是发达国家还是发展中国家，现实经济中的技术进步一般是有偏技术进步，即假定要素投入比例不变时，技术进步对不同要素边际产出的提高程度是非均等的。因此，本文将资本深化、有偏技术进步纳入要素收入份额与全要素生产率增长的研究框架，并重点围绕以下问题展开研究：资本深化与有偏技术进步是否对要素收入份额和全要素生产率产生影响，其作用机制是什么？资本要素和劳动要素替代性如何，技术进步是否存在偏向性？要素收入份额变动是否会对全要素生产率产生影响，其作用机制是什么？在中国经济高质量发展的关键时期，通过研究上述问题可以为选择适宜的要素禀赋结构变动、技术进步路径和要素收入份额进而提高全要素生产率，提供理论支撑。

二、文献综述

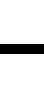
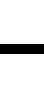
综上所述，在要素收入份额和全要素生产率的已有研究中，存在以下不足：一是已有研究以单位替代弹性和中性技术进步假设条件为主，无法有效地将要素禀赋结构变动纳入要素收入份额和全要素生产率研究，从而容易忽略资本深化对两者的影响；二是虽然部分学者开始从有偏技术进步视角研究资本深化对要素收入份额和全要素生产率的影响，但已有研究一般采用初始CES生产函数直接进行拓展分析，由于初始CES生产函数的部分参数意义不明确，导致无法从理论上清晰展现资本深化、有偏技术进步对要素收入份额和全要素生产率的作用机制。有鉴于此，本文在已有文献的基础上，采用标准化后的CES生产函数，在有偏技术进步视角下，研究资本深化对要素收入份额变动及全要素生产率的影响机制。

三、理论分析

本部分在标准化CES生产函数的基础上，将资本深化、有偏技术进步纳入要素收入份额和全要素生产率分析框架，对相关变量之间的作用机制进行理论分析。

(一)要素收入份额变动的理论分析

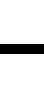
(1)

上式中，Yt表示产出值；Kt、Lt分别表示资本要素和劳动要素投入值；Akt(Alt)表示技术进步过程中资本(劳动)增强型技术进步；假设其它条件不变的情况下，Akt(Alt)的数值越大，单位资本(劳动)产出越多，因此AktKt(AltLt)也可以定义为以效率衡量的综合资本(劳动)要素投入。σ为综合资本要素与综合劳动要素的替代弹性，表示综合要素边际产出之比随要素报酬率之比的变化而变化的程度。当σ>1时，综合资本要素和综合劳动要素之间替代性较好，两者总体呈替代关系；当σ<1时，综合资本要素和综合劳动要素之间的替代性较差，两者总体呈互补关系。Y0、K0、L0、Ak0、Al0为标准化基准点，θ0为标准化基准点上资本要素收入份额。

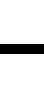
(2)

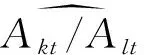
(3)

从(3)式可以看出，要素收入份额比与基准点要素收入份额的偏离和要素替代弹性σ直接相关。与已有研究相比，使用标准化后的CES生产函数分析资本深化、有偏技术进步对要素收入份额的作用机制，可以清晰展现要素替代弹性、资本深化、有偏技术进步与要素收入份额之间相互关联性。为了更直观的分析资本深化、有偏技术进步对资本—劳动收入份额比的影响，对(3)式取对数后，进一步对时间取全微分得到资本要素和劳动要素收入份额之比变动率：

(4)

(4)式显示，当σ≠1时，即在非单位替代弹性下，要素收入份额比与基准点要素收入份额比的偏离将受到资本深化和有偏技术进步的影响。进一步分析可知，资本—劳动收入份额比对资本深化以及净要素增强型技术进步指数的弹性为常数，弹性正负取决于σ值。当σ>1时，资本—劳动收入份额比对资本深化以及净要素增强型技术进步指数的弹性为正；当σ<1时，资本—劳动收入份额比对资本深化以及净要素增强型技术进步指数的弹性为负。

(二)全要素生产率的分解框架

对标准化CES生产函数取对数后，在σ=1点进行二阶泰勒展开，然后继续取全微分，并在剔除资本和劳动要素投入增长的影响，可以得到全要素生产率增长率的表达式：

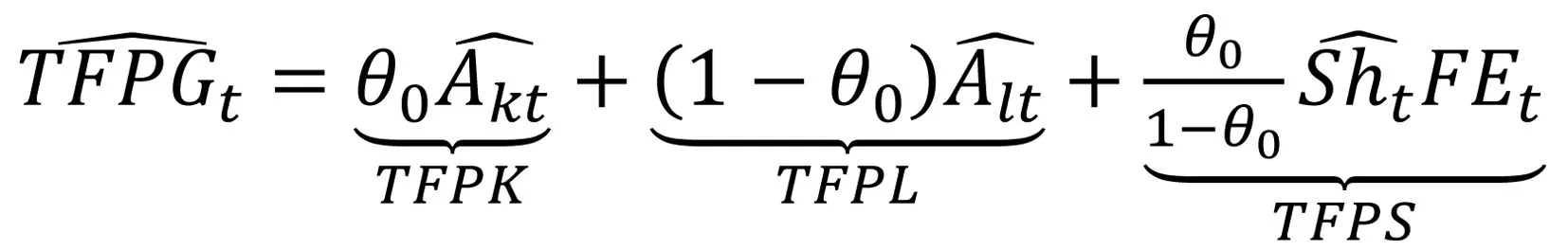
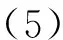
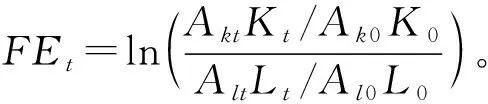
(5)式中，将全要素生产率增长率分为3个部分:纯资本增强型技术进步的增长效应TFPK、纯劳动增强型技术进步的增长效应TFPL以及资本—劳动收入份额比的变化对全要素生产率增长率的影响TFPS。从(5)式可以看出，前两项的系数θ0与(1-θ0)均为正，因此对全要素生产率增长率都是直接促进作用，即纯资本增强型技术进步和纯劳动增强型技术进步的增长都能直接促进全要素生产率增长；后一项从生产角度揭示了要素收入份额与全要素生产率的关系，其对全要素生产率增长率的影响作用受到FEt的影响。由于AktKt、AltLt表示以效率衡量的资本和劳动的综合要素投入，因此本文将FEt定义为综合要素结构变动值，代表了当期综合要素结构相对于基准点时结构的变动情况。当FEt>0时，相对于基期，综合资本要素的变动比综合劳动要素的变动程度大，即综合要素结构变动偏向资本；当FEt<0时，情况相反，综合要素结构变动偏向劳动。具体来看，资本—劳动收入份额比对全要素生产率增长率的影响取决于综合要素结构变动值FEt。当FEt>0时，即当综合要素结构变动偏向资本时，通过(3)式可知，当要素之间呈互补关系时，此时资本—劳动收入份额比基准点时的份额低，提高资本—劳动收入份额比，符合综合要素结构变动趋势，有助于充分发挥要素的产出效率，从而提高全要素生产率；当FEt<0时，即当综合要素结构变动趋势偏向劳动时，此时资本—劳动收入份额比基准点时的份额高，降低资本—劳动收入份额比，符合综合要素结构变动趋势，有助于充分发挥要素的产出效率，从而提高全要素生产率。

四、参数估计方法、实证模型设定与数据说明

(一)参数估计方法

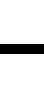
(6)

上式中的γi,λi(i=k,l)分别表示资本要素和劳动要素的技术进步年均增长率和曲率。

(7)

在完全竞争市场的假设条件下，通过(7)式推导资本要素需求和劳动要素需求的一阶条件，得到(8)式、(9)式：

(8)

(9)

将(7)式、(8)式、(9)式组成非线性联立方程组进行标准化系统估计，估计相应参数。

(二)实证模型设定

根据上文理论分析，为了验证资本深化以及净要素增强型技术进步对要素收入份额的影响，设定相应的实证模型。由于资本深化过程一直持续，有明显的时间趋势，且经面板单位根检验方法检验后，验证属于一阶单整序列。为了消除资本深化的时间趋势，同时根据文中资本—劳动收入份额比的理论分析，建立相应的静态实证检验模型：

shit=α11+α12cdit+α13dit+β1Xit+μi+εit

(10)

鉴于资本—劳动收入份额比具有大体稳定的特征，因此可能存在内生性问题，为了提高实证估计结果的可信性和稳健性，同时建立动态实证检验模型：

shit=α21+α22shit-1+α23cdit+α24dit+β2Xit+μi+εit

(11)

上式中，shit-1为资本相对收入份额变动率的一阶滞后。

为了进一步验证前文理论部分要素增强型技术进步、要素收入份额变动对全要素生产率增长率的影响，除了采用本文中的测算方法对全要素生产率进行直接测算分解外，同时采用其他测算方法得到的全要素生产率增长率与要素增强型技术进步、要素收入份额变动建立相应的实证检验模型：

gtfpit=α31+α32gakit+α33galit+α34lshit+α35lsh2it+μi+λt+εit

(12)

gtfpit是采用CES直接计算的SRA方法(19)封永刚、蒋雨彤、彭珏：《中国经济增长动力分解:有偏技术进步与要素投入增长》，《数量经济技术经济研究》2017年第9期。和MALMQUIST方法测算得到两种全要素生产率增长率。其中，CES直接计算的SRA方法因未使用泰勒展开，没有直观展现要素收入份额对全要素生产率增长率的影响，因此可以用来实证分析方法检验要素收入份额对全要素生产率增长率的影响。MALMQUIST方法既未直观展现要素增强型技术进步、要素收入份额变动对全要素生产率增长率的影响，且包含非完全技术效率，因此适用于要素增强型技术进步、要素收入份额对全要素生产率增长率影响的实证检验。上式中的gakit表示资本增强型技术进步变动率；galit表示劳动增强型技术进步变动率；lshit表示资本-劳动收入份额比的对数值；lsh2it表示lshit的二次项；μi表示个体固定效应；λt表示时间固定效应；εit表示随机扰动项。

(三)变量界定与数据来源

(1)总产出Y，采用收入法核算的GDP表示。收入法GDP等于劳动者报酬、净税收、固定资产折旧和营业盈余之和。利用GDP平减指数进行平减，基期为1990年。

(2)劳动要素数量L，采用年末就业人员人数表示。

(4)劳动要素报酬率w。除了采用收入法GDP中的劳动者报酬以外，由于本文中不涉及政府部门，所以对收入法GDP中的净税收也按一定比例归到劳动要素报酬和资本要素报酬中，具体划分比例参照戴天仕和徐现祥(21)戴天仕、徐现祥：《中国的技术进步方向》，《世界经济》2010年第11期。的方法。劳动要素报酬率=劳动要素报酬/劳动要素数量。

(5)资本要素报酬率r。本文假定为完全竞争情况，资本报酬和劳动报酬之和等于总产出，因此用总产出减去劳动者报酬之差比上资本存量作为资本价格，即资本要素报酬率=(收入法GDP-劳动要素报酬)/资本存量。

相关变量定义及统计性描述见表1所示。

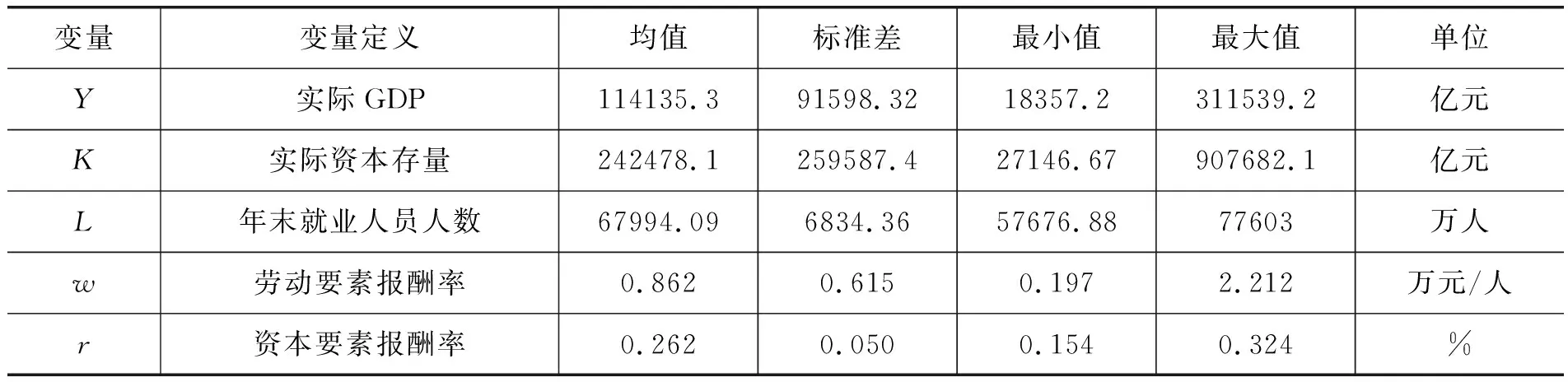
表1 变量定义及统计性描述

五、实证结果与分析

(一)参数估计结果及分析

表2 中国CES生产函数参数估计结果

(二)增长核算结果及分析

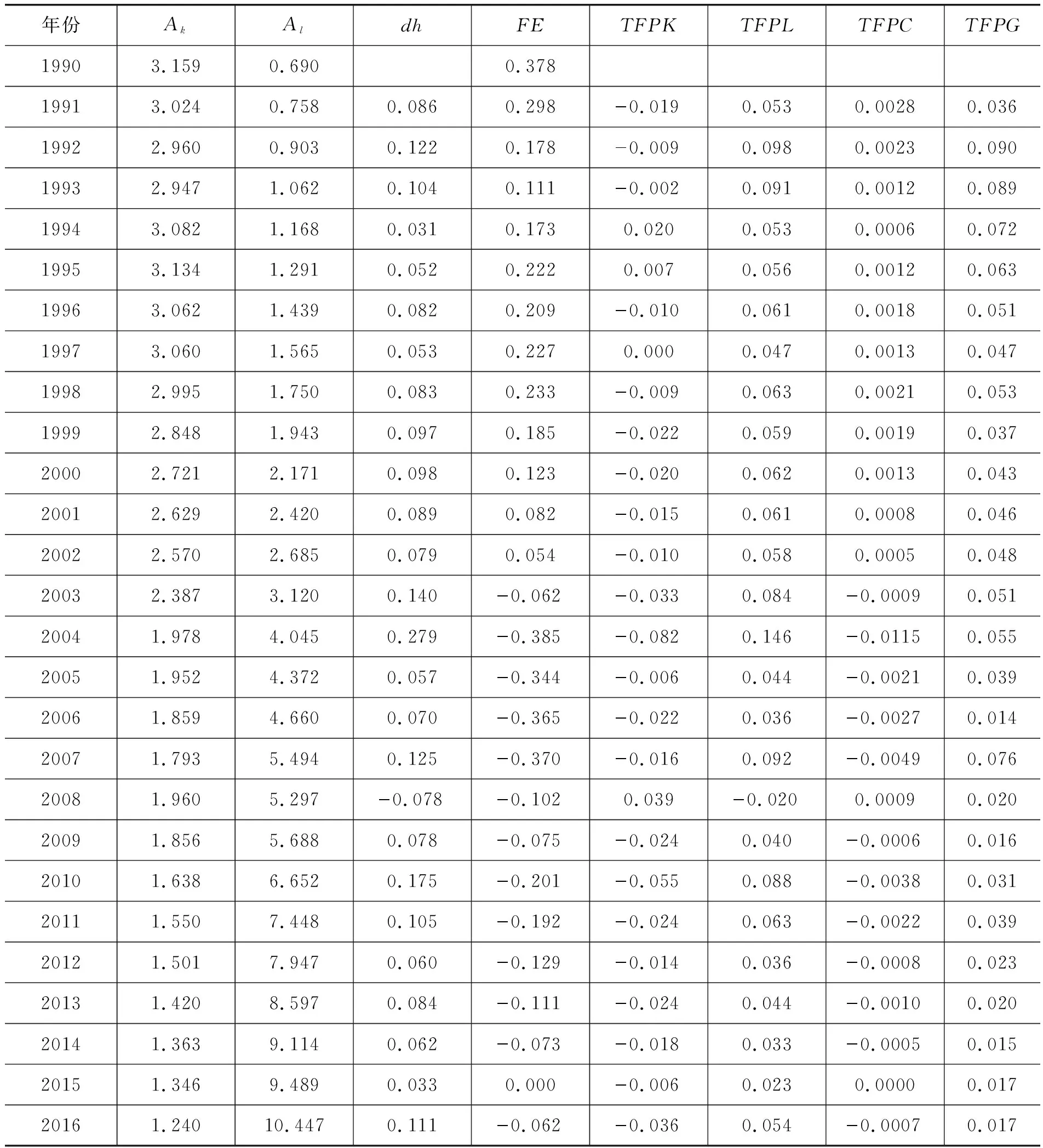
表3 中国分年份技术进步偏向及全要素生产率增长率分解表

(三)回归估计结果及分析

为了提高实证估计结果的稳健性和可信性，对静态实证方程(10)式采用OLS混合估计和FE固定效应两种估计方法进行回归；对动态实证方程(11)式采用一阶段稳健型GMM估计和二阶段GMM估计两种方法进行回归。使用动态GMM估计方法的前提是差分后的扰动项不存在二阶(或更高阶)自相关，因此本文给出了一阶、二阶序列相关检验的P值。以上估计结果分别在表4中的四列中展示。其中，OLS为OLS混合估计结果；FE为FE固定效应估计结果；GMM_1为一阶稳健型GMM估计结果；GMM_2为二阶段GMM估计结果。

从表4可以看出，无论在静态估计还是动态估计中，核心解释变量均在5%水平上显著，且符号完全一致，对本文理论进行了很好的实证检验。具体来看，资本要素收入份额变动率一阶滞后项shit-1系数为负，这说明资本—劳动收入份额比长期中具有大体稳定性特性；资本深化速度cd系数为负，说明资本—劳动收入份额比对资本深化的弹性为负。这与前文理论分析一致，在要素替代弹性小于1的情况下，资本深化对资本—劳动收入份额比的影响为负，且资本深化速度越快，资本—劳动收入份额比减少的速度越快；d的系数为正，表明技术进步偏向资本对资本—劳动收入份额比的影响为正，且偏向资本程度越高，资本—劳动收入份额比增加的速度越快。控制变量的结果与常识一致，具体来说，资本—劳动收入份额比对出口占比的半弹性系数为正，即出口份额占比越高，资本—劳动收入份额比增加的速度越快；资本—劳动收入份额比对第三产业占比及外商投资占比的半弹性系数均为负值，说明第三产业占比及外商投资占比越高，资本—劳动收入份额比减少的速度越快。

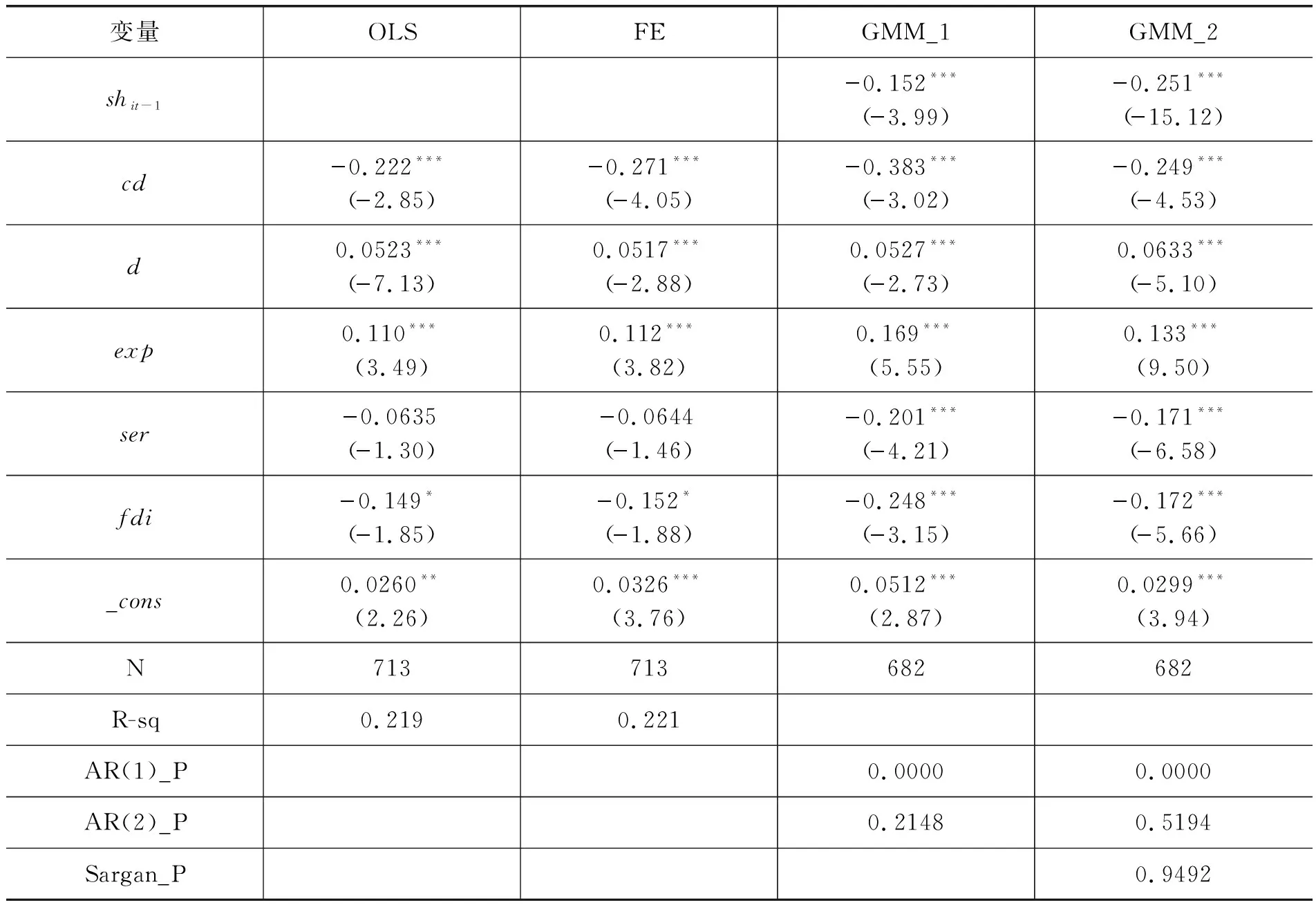
表4 资本深化和有偏技术进步对要素收入份额影响

表5的结果显示，两种因变量下的估计系数均显著，且符号方向一致。具体来看，资本增强型技术进步增长率以及劳动增强型技术进步增长率的系数均为正，说明要素增强型技术进步确实存在对全要素生产率增长率的正向促进作用。资本—劳动收入份额比的对数值及其二次项的系数均为负，说明资本—劳动收入份额比对全要素生产率增长率的影响显著为倒U型，这与前文理论分析完全一致，在要素之间总体呈现互补关系时，要素收入份额比与长期基准点的偏离可能从供给和需求两个方面对全要素生产率产生负向影响。

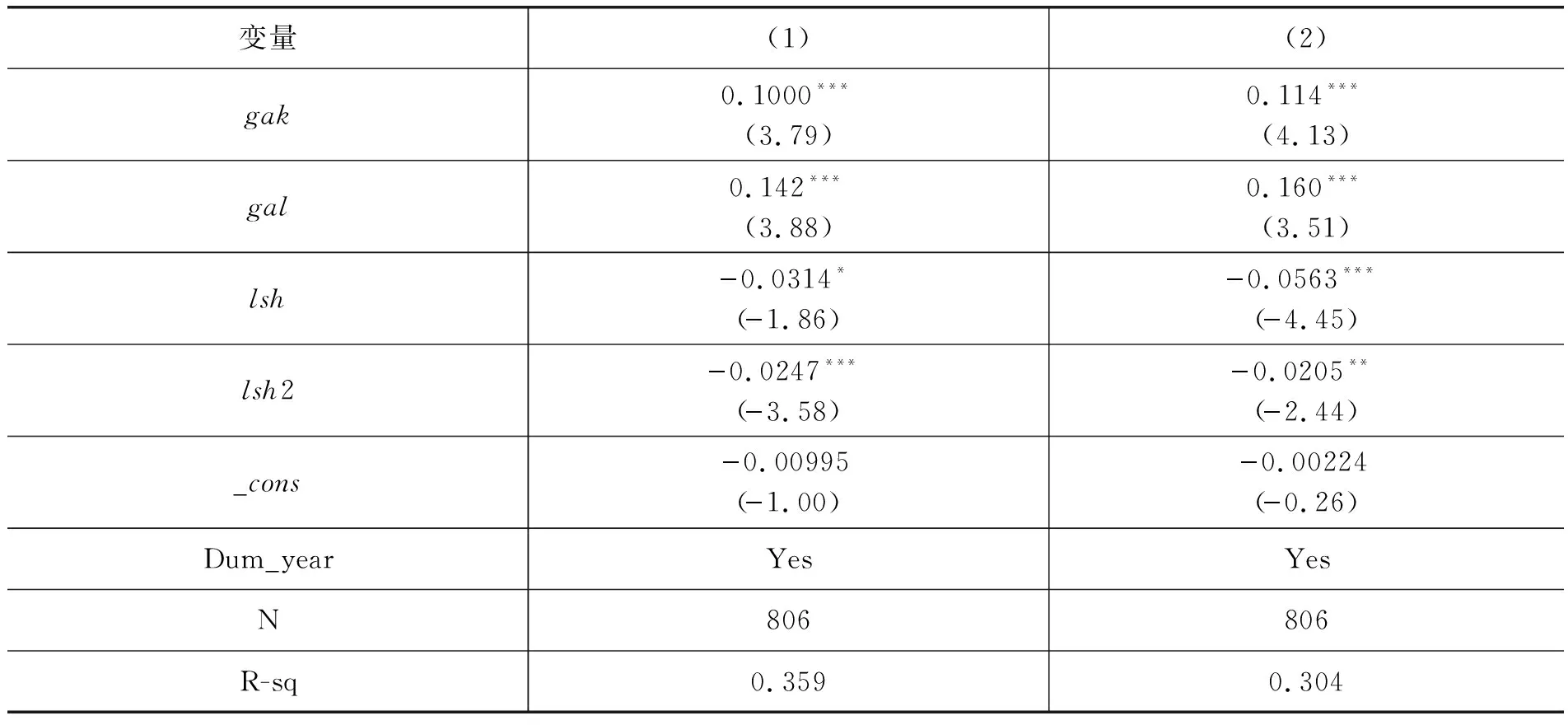
表5 要素增强型技术进步和要素收入份额变动对全要素生产率的影响

六、主要结论和政策含义

本文通过拓展标准化CES生产函数，从技术进步偏向视角分析了要素收入份额偏离长期稳定基准点的原因及其对全要素生产率的影响。理论分析显示，单位替代弹性下的结论与传统经济分析一致，要素收入份额会长期稳定在基准点；由于现实中要素之间存在非单位替代弹性，综合要素结构变动会影响要素收入份额，其中综合要素结构变动由资本深化和有偏技术进步共同决定；无论从供给还是需求角度来看，要素收入份额长期大体稳定有助于提高全要素生产率，对于经济发展质量提升有重要意义。实证分析发现：中国整体及大部分省级区域的综合资本要和综合劳动要素替代弹性小于1，要素之间总体呈互补关系；无论是区间总体偏向还是分年份偏向来看，中国整体及大部分省市的技术进步基本偏向资本；过快的资本深化速度可能导致了资本要素产出效率未能得到充分发挥，反而使综合资本要素变动相对过低，在综合要素互补情况下，提高了资本—劳动收入份额；资本—劳动收入份额比对全要素生产率增长率的影响为倒U型，因此资本—劳动收入份额比与长期稳定基准点的偏离会对全要素生产率增长率造成不利影响。

基于以上研究结论，提出以下相应政策建议：一是继续维持资本深化态势。随着国民经济实力的不断增强，资本要素相对越来越充足，使用资本要素替代劳动要素是经济发展的必然趋势。在当前全球疫情的冲击和影响下，审时度势的采取积极有为的财政政策，适度增加货币供给，进一步推动供给侧结构性改革，有助于增强经济内生动力，实现经济社会持续健康发展。但同时应该着重强调财政政策有效性，坚决防止政策性低效率或无效率资本形成。二是提高资本投资质量，提升资本要素产出效率。在资本深化持续进行的事实下，注重实现集约式、高质量有效投资，提高机器设备科技含量，提高资本要素产出效率，提高资本要素和劳动要素的替代性，实现要素结构更加匹配，促进要素收入份额稳定和经济发展质量提升。三是加大教育培训力度，继续提升人力资本红利水平。加大对劳动者的教育和培训投入，扭转劳动力数量拐点影响，继续提高人力资本红利水平。同时通过改革税收制度、增加公共支出、加大转移支付力度等措施，充分发挥再分配过程中的调节作用，维持要素收入份额长期大体稳定，防止要素收入份额大幅波动对经济产出效率产生不良影响。