浅谈含参数一元二次不等式的解题方法

◎许 媛 高 静 （北华大学数学与统计学院，吉林 吉林 132001）

一、含参数的一元二次不等式

一元二次不等式，是指含有一个未知数且未知数的最高次数为2 的不等式［1］.它的一般形式有：

ax2＋bx＋c＞0，ax2＋bx＋c＜0 （a，b，c均为常数）.

含参数的一元二次不等式应为含有一个未知数且未知数的最高次数为2，其中二次项系数、一次项系数、常数项均可能含有参数的不等式.

含参数的一元二次不等式范围广，题型多变，不易于从基本一元二次不等式解法中获取解题思路和方法.根据国家高中数学课程标准的有关要求，此类问题是大型考试中重点研究和考查的内容.据有关专家统计，在大型考试中此类题型出现的概率高，并且其出错率也高.笔者经过多年的整理分析发现，考试中常出现的题型有四种：二次项系数不含参数的一元二次不等式、二次项系数含有参数且能被十字相乘的一元二次不等式、二次项系数含有参数且不能被十字相乘的一元二次不等式、恒成立的含参数一元二次不等式.本文针对上述四种题型，进行详细研究，通过分析题型特点，分情况讨论，提出适当的解题方法，并给出解题步骤.

二、含参数的一元二次不等式四种题型解法的讨论

题型1x2＋ax＋a＜ (＞ )0，a为参数型的含参数一元二次不等式［2］

特点：此题型具有二次项系数不含参数，一次项系数和常数项所含参数相同的特点，可以通过十字相乘法化简.

常见问题：十字相乘法使用不当，使得化简出现错误.

基本解法：十字相乘法、分类讨论法、图像法.

具体步骤：（1）利用十字相乘法对不等号左边的多项式进行因式分解；（2）再令其等于零，即变成一元二次方程的形式，解出方程的两个根；（3）比较两个根的大小，分情况进行讨论，并配以相应的二次函数简图，加深理解；（4）最后按参数的取值情况，写出对应的解集.

下面通过例1 具体说明题型1 的解题步骤.

例 1求不等式x2－(a2＋a)x＋a3＜0 的解集.

思路分析此不等式虽然含有参数，但是经过思考不难发现此不等式左边的多项式可以通过化简，转换成我们常见一元二次不等式的形式求解，只需注意分情况讨论时，不要丢失情况即可.

解利用十字相乘法对x2－（a2＋a）x＋a3进行因式分解，即x2－（a2＋a）x＋a3＝（x－a2）（x－a）.

再令（x－a2）（x－a）＝ 0，解得x1＝a2，x2＝a.

比较a2与a的大小，分情况讨论：

（1）当a2＝a时，解得a＝0 或a＝1，如图 1，x∈∅；

（2）当a2＞a时，即a2－a＞0，解得a＜0 或a＞1，如图 2，｛x｜a＜x＜a2｝；

（3）当a2＜a时，即a2－a＜0，解得 0＜a＜1，如图 3，｛x｜a2＜x＜a｝.

综上可得，原不等式的解集分三种情况：当a＝0 或a＝1 时，x∈∅；当a＜0 或a＞1 时，｛x｜a＜x＜a2）｝；当 0＜a＜1 时，｛x｜a2＜x＜a｝.

图1

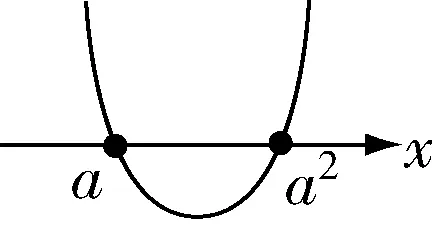
图2

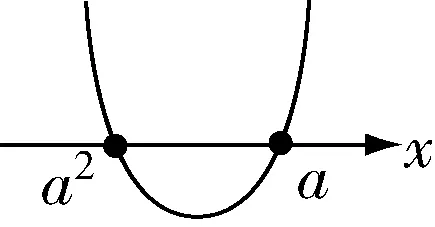
图3

题型2ax2＋ax＋c＜ (＞ )0，其中a（a≠0）为参数，c为常数型的含参数一元二次不等式［3］

特点：此类不等式具有二次项系数和一次项系数含参数且相同，但常数项不含参数的特点，可以通过十字相乘法进行化简.

常见问题：未对二次项系数进行讨论.

基本方法：分类讨论法、十字相乘法、图像法.

具体步骤：（1）讨论二次项系数a的取值是否为零；当a＝0 时，按照一元一次不等式求x的解集；当a≠0 时，即参数a＜0 或a＞0 时，应先将不等号左边的多项式用十字相乘法进行因式分解，再利用一元二次不等式与一元二次方程之间的关系得出两个根；（2）讨论、比较两个根的不同情况，然后利用图像法求得相应的解集；（3）按参数的取值情况，写出对应的解集.

下面通过例2 具体说明题型2 的解题步骤.

例2 求不等式ax2－（a＋1）x＋1＜0（a＜1）的解集.

思路分析虽然不等式后面给出了a的取值范围，但在进行分类讨论时，首先我们需要分两大类进行讨论，即在a＝0 和a≠0 时的情况下讨论，最后在a≠0 的前提下，再详细地分类讨论即可.具体解题步骤如下：

解当a＝0 时，－x＋1＜0，解得x＞1；当a≠0 时，将不等式左边十字相乘，得（x－1）（ax－1）＜0，（x－1）（ax－1）＝ 0 的解为由于无法比较两个根的大小，且由a≠0我们可以得出这两种情况，即a＜0 或a＞0，所以详细的分类讨论如下：

当 0＜a＜1 时如图 4，解得

当a＜0 时如图 5，解得

综上， 当a＝ 0 时， ｛x｜x＞ 1｝； 当 0 ＜a＜ 1 时，当a＜0 时

图4

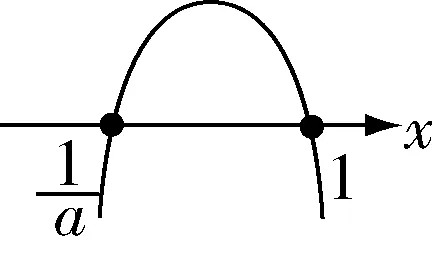
图5

题型 3ax2＋cx＋a＞（＜）0，其中a为参数，c为常数型的含参数一元二次不等式［4］

特点：此类不等式具有二次项系数和常数项含参数且相同，而一次项系数不含参数的特点.

常见问题：错误使用十字相乘法求解，导致解题失败.

基本做法：分类讨论法、利用根的判别式的情况分析的方法.

具体步骤：（1）讨论参数a是否为零，当a＝0 时，即解一元一次不等式，从而求出解集；当二次项系数所含的参数不为零时，进一步讨论；（2）在参数a≠0 的情况下，利用根的判别式的情况进行分类讨论，即讨论当Δ＝0，Δ＞0，Δ＜0时所对应的解集；（3）综合各参数的范围，写出对应的解集.

针对题型3 与题型1、2 所使用的方法有明显不同，下面通过例3 来说明.

例 3求不等式ax2＋2x＋a＞0（a∈R）的解集.

思路分析一方面，要分析这个一元二次不等式的左边能否正确地利用十字相乘法进行因式分解；另一方面，当它无法进行因式分解时，要转换思路，从而求出解集.解题步骤如下：

解当a＝0 时，则 2x＞0，解得x＞0.

当a≠0 时，Δ＝4－4a2，即有

①Δ＝0，即4－4a2＝0，解得a＝±1，即当a＝1 时，x2＋2x＋1＞0，如图6，解集为｛x｜x≠－1｝ ，当a＝－1 时，－x2＋2x－1＞0 ，如图7，解集为x∈∅.

②Δ＞0，即 4 (1 －a2)＞0 时，则有当－1＜a＜0 时，如图 8，解集为当 0＜a＜1 时，如图9，解集为

③Δ＜0，即 4－4a2＜0 时，则当a＞1 时，如图 10，解得x∈R，当a＜－1 时，如图 11，解得x∈∅.

综上可得，当a＝0 时当a＝－1 或a＜－1时，x∈∅；当a＝ 1 时当－1＜a＜0 时，x∈当 0 ＜a＜ 1 时，x∈当a＞1 时，x∈R.

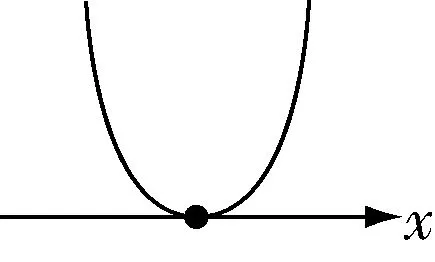
图6

图7

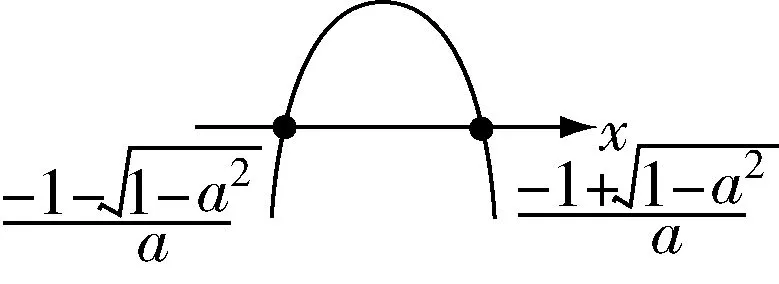
图8

图9

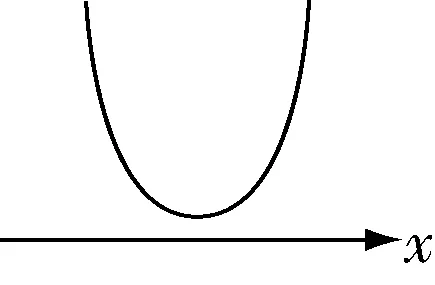
图10

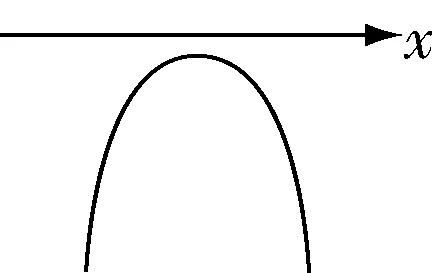
图11

题型4ax2＋ax＋c＞ (＜ ) 0(x∈R)，其中a为参数，c为常数，解集是全体实数型的含参数一元二次不等式

特点：此类不等式不求含参数一元二次不等式的解集，而是通过已知解集来求所含参数的取值范围.

常见问题：忽略解集x∈R，错用题型2 的解题方法，导致解题失败.

基本做法：分类讨论法、“开口＋判别式”法.

具体步骤：（1）讨论参数a是否为零，当a＝ 0 时，要看常数c是否大于（小于）0 恒成立，以此来取舍参数a的取值情况.（2）当a≠0 时，将ax2＋ax＋c＞（＜）0 转化为二次函数的恒成立问题，利用二次函数f（x）＝ax2＋bx＋c（a≠0，x∈R），f（x）＞0 对x∈R 恒成立⇔a＞0 且Δ＜0 和f（x）＜0 对x∈R 恒成立⇔a＜0 且Δ＜0 的两条结论来判断参数a的取值情况.（3）综合情况，写出参数的取值范围.

题型4 和前三种求解的内容有很大的区别，通过下面的例题来说明.

例 4已知不等式（a－2）x2＋（a－2）x＋1＞0（x∈R）恒成立，求参数a取值范围.

思路分析此不等式不是二次函数的形式，不能直接利用“开口＋判别式”法，所以做题时要注意分类讨论.具体解题步骤如下：

解（1）当a－2＝0 时，解得a＝2，原不等式可化为 1＞0，满足对于一切的x∈R，原不等式恒成立.

（2）当a－2≠0 时，利用“开口＋判别式”法，有

（3）综合（1）和（2），于是有a∈［2，6）.

上述例子的比较分析：例1 和例2 对比来看，基本解法是相似的，但例2 的难度加深，更能锻炼学生的思维能力，例3 和例1、例2 相比较而言，巧妙地运用了根的判别式方法求解集，而例4 则是完全不同于前三道例题的，例4 是已知了解集，求解的是参数的取值范围，前三道例题是通过讨论参数的取值情况求解不等式的解集，并且例4 在解题方法上也有了变化，它是以“恒成立”为前提，巧妙地与二次函数的恒成立问题联系起来，并借助其结论进行解题.这样设置例题不容易给学生造成思维定式，可以达到丰富学生的解题方法的目的.

结语：含参数一元二次不等式的解法是高中数学的难点之一，具有一定的研究价值.本文所阐述的四种题型及解题方法有利于学生提高自身的学习效率，从而激发学生的学习兴趣，使学生在考试中面对此类问题时能够得心应手，降低出错率，为高中学生学习数学提供了行之有效的方法.