基于混合式教学模式的高等数学教学探究

张遥

摘要：本文从信息化背景出发，结合高等数学课程的特点和高职院校学生的实际情况，以“线上+线下”混合式教学模式构建智慧课堂，从课前准备、课堂实施、课后提升三个阶段深入探讨了导数概念的教学设计。通过“六导”环节将线上、线下教学联系起来，引导学生自主学习、合作探究，提高教学质量。

关键词：高等数学;混合式;高职院校;智慧职教

一、教学分析

整个教学过程遵循“以学生为主体，以教师为主导，以知识为主线，以问题为主轴，以提高数学核心素养为主旨”的原则，采用基于问题解决的“探究式”教学方式，让学生参与到教学全过程中，充分体现了教、学、思、做的一体化。微课视频、专业案例情境导入让概念的呈现从陌生变为熟悉，动画演示、数学软件辅助作图让问题的探究从抽象变为形象，课堂详细讲解、讲练结合的方式让内容的解析从模糊变为清晰，小组讨论、自主探究让知识的学习从困难变为容易。

二、教学设计

教学设计主要分为课前准备、课堂实施、课后提升三个阶段。

（一）课前准备阶段

通过智慧职教发布课前学习任务：观看微课视频，收集生活中有关导数的实例，上传至智慧职教平台，并投票评选出“最佳案例”。在锻炼学生自主学习能力的同时便于教师了解学生对导数的理解程度。

（二）课堂实施阶段

课堂实施阶段首先是教师引导学生复习极限知识，为学习导数的概念做好铺垫。然后是“六导”环节。

环节一：情境导入，设疑激趣。

播放我国首列自主研发的无网超能有轨电车“光谷量子号”的视频，通过视频引发学生对两个细节问题的思考：有轨电车运动过程中瞬时速度的变化及通过弯道时每一点的切线斜率。结合学生的专业背景提出问题，激发学生的学习兴趣，让学生感受到数学的实用性。再深入挖掘案例中的德育元素进行思政教育，通过介绍“光谷量子号”有轨电车在技术上的创新与突破，激发学生的自豪感、自信心，培养学生的爱国主义情怀。

环节二：动画导学，操作探究。

针对两个问题提炼出数学模型，在智慧职教发布课中学习任务：

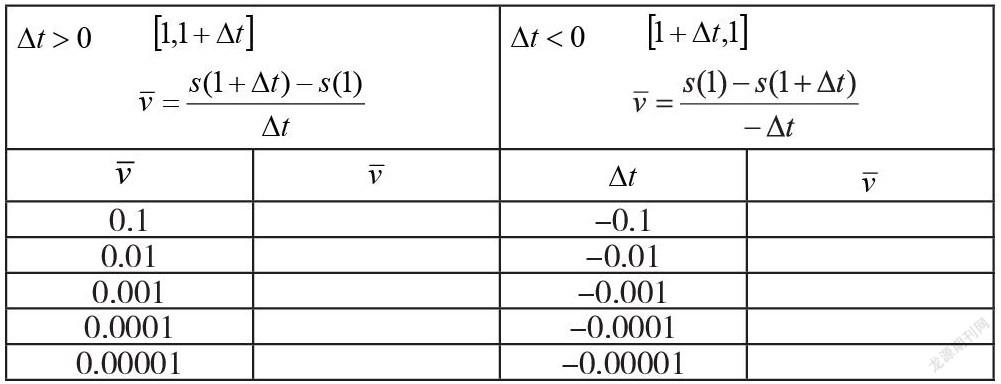
（1）假如有轨电车的位移s（m）与时间t（s）的关系满足：s（t）=2t2-t+5。请以小组为单位填写以下表格，观察平均速度的变化趋势，并给出t=1s时瞬时速度的求解思路。

，在内，平均速度为： ，在内，平均速度为：

0.1 -0.1

0.01 -0.01

0.001 -0.001

0.0001 -0.0001

0.00001 -0.00001

（2）请用描点法画出位移函数的图像，在图像上标出时间为t=1s、t=2s的两点，连接两点求出对应割线的斜率，并思考如何确定在t=1s时曲线对应的切线斜率。

使用动画演示，将极限逼近的思想动态模拟出来，形象直观的展示更易于学生理解，这就化解了教学难点。先动画演示时刻附近的平均速度变化情况，以平均速度为突破口，当时，平均速度的极限就是物体在t0时刻的瞬时速度，即：。再动画演示曲线割线逐渐逼近切线的过程，从极限的角度认识切线：。最后，通过案例让学生体会以“不变”代“变化”，以“直”代“曲”的转化思想。

环节三：概念导析，类比探索。

针对以上2个问题安排学生进行小组讨论、归纳分析，引导学生运用从特殊到一般的思想方法探究函数瞬时变化率的问题：求函数增量与自变量增量比值的极限，也就是在某一点处的导数：。并进一步类比推出导函数的概念：。这一环节锻炼了学生观察、类比、归纳、概括的能力，也是理解导数概念至关重要的一环[2]。

环节四：拓展导用，提炼方法。

引导学生总结用定义计算导数的步骤：

1.“一差”：;

2.“二比”：;

3.“三极限”：。

再回归问题情境，通过例题和作图引导学生总结导数的几何意义，强化对知识的理解。例题如下：某飞行器在发射后的一段时间内，运动方程为：h（t）=2t3+1，其中，h的单位为m，t的单位为s。求出：（1）该飞行器在t=2s时的瞬时速度。（2）该函数曲线在点（1，6）处的切线方程和法线方程。由具体实例到抽象定义最后又回到具体实际问题的过程，强化了学生对知识的理解，也诠释了数学来源于生活又服务于生活。

环节五：强化导练，巩固提高。

课堂练习有助于学生巩固重点、突破难点、内化知识。本环节在智慧职教发布学习任务：请在规定时间内分小组完成課堂练习题，比一比哪组的得分最高。在线练习、讲练结合充分凸显了学生的主体地位，在做中学的过程培养了学生正确的竞争意识和团队合作能力。

环节六：总结导思，评价反馈。

最后引导学生从知识、方法、能力三个层面对本次课所学的内容进行归纳小结。在理清知识点、提炼数学方法和提升综合能力的同时，便于学生养成总结反思的良好习惯。采用多元化评价方式全面、公正、客观评价学生的课堂表现，通过学生投票的方式选出“最佳小组”。

（三）课后提升阶段

课后设置阅读、测验、实践等分层作业兼顾到不同层次学生的学习需求。通过由浅入深、由易到难、由简到繁的作业题帮助学生查缺补漏，理解与巩固知识。

参考文献：

[1] 孙珊珊.基于翻转课堂教学模式的导数概念的教学设计[J].科技经济导刊，2017（14）：141-142.

[2]李少云，李融.基于抛锚式教学模式的导数概念设计[J].天津电大学报，2020，24（02）：31-33.