巧妙分类 破解困局

金玺

摘要：高考数学试卷的压轴题倾向于含参导数题型，由于此类数学题的破解需要考生讨论分析，这在一定程度上拓展了学生数学思维，锻炼了学生解题能力。基于此，本文针对含参高考导数题巧妙分类，并总结破解含参高考导数题困局的要点。旨在为高考试题命题小组在试题设置中提供思路，真正培养高考生数学核心素养。

關键词：高中数学;含参导数题;压轴题;求解分析

引言：近年来，含参高考导数题成为高考的热点题型，同时，考生之间在这类题型求解中拉开分数差距，为了让学生掌握这类压轴题解法，提高学生高考数学成绩，本文针对该论题重点分析。可见，含参高考导数题的分析求解类论题具有探究性意义和现实性意义，具体内容如下。

1.含参高考导数题巧妙分类

1.1基于极限值和特定区间位置关系

导数是函数的组成部分，由于函数题存在难易之别，所以划分成简单函数、复杂函数两种[1]。对于复杂函数，往往是因为导数、含参导数的借入而增加解题难度，极限值求解、区段位置关系判断时，要求考生具备缜密的逻辑体系，并对所学知识点综合化、灵活化运用。

1.2基于两根大小

判定根的大小关系是含参导数题型的一种，破解这类题时，先确定讨论目标、界定讨论范围，接下来掌握分类标准，为类别划分提供依据。由于题目信息不同，所以必要情况下分级分类，这是解题的关键。最后归纳结论。

1.3基于判别式

情形划分是含参高考导数题的普遍考法，因此，需要考生扎实巩固基础知识，掌握解题技巧。尽可能在短时间内准确求解，留有充足的校审时间，降低含参导数压轴题的丢分概率。

1.4基于根在定义域存在与否

函数定义域是函数性质界定的重要依据，当定义域发生改变，则函数性质随之变化[2]。对于考生来说，应在这类含参导数题型解答中认真审题，准确判断定义域变化，确定根是否在定义域内，避免解题方向发生偏颇，尽可能得分。

2.破解含参高考导数题的困局

2.1求极限值

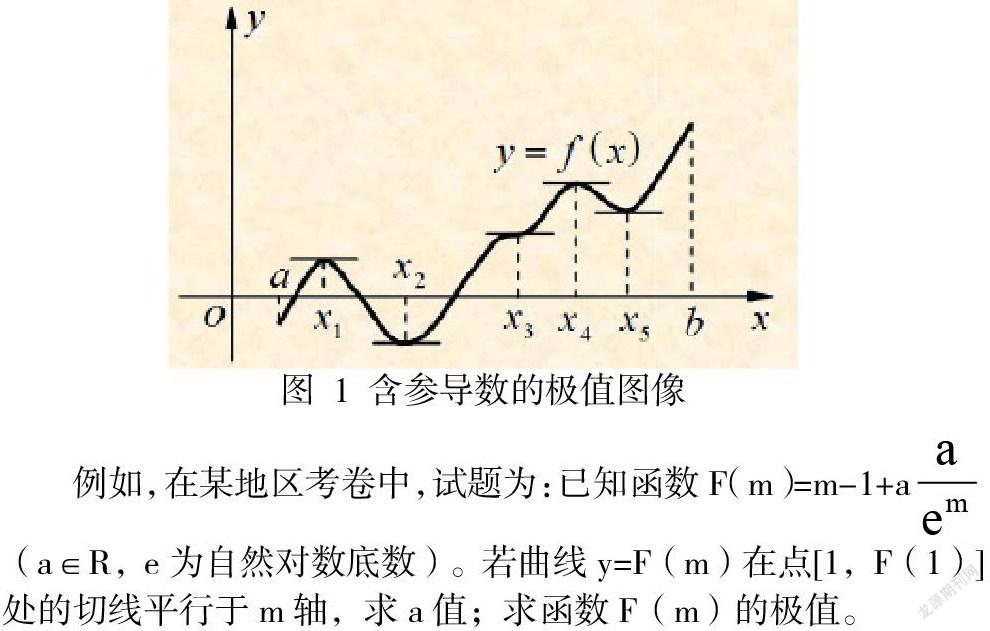
含参导数极值问题求解时，考生应具备函数图像观察能力，从图像中捕捉解题的关键信息，在图1中，极大值分别是f（x1）和f（x4），极小值为f（x2）和f（x5）。从中可以看出，极值点能否准确确定，这对极限值求解有重要影响。

2.3含参导数求解

含参导数作为高考压轴题的重点题型，也是高中学生在数学解题中的便捷工具，这类题型对师生数学思维能力和讨论能力提出较高挑战，实际解答时，学生应强化自信心，认真分析题干，并灵活运用导数知识[3]。实际上，导数的定义和性质十分重要，即便含参导数题型多样变化，是实质上考察学生对导数性质的考察，在极限值求解、根的大小判断、判别式关系、根是否在定义域等四种类型题的解答中，需要考生深入理解含参导数的含义和性质，在解题过程中理顺思路、发现解题的关键点，避免失分。

结论：综上所述，高考数学试题的压轴提醒多为含参导数题，解答这类数学题时，考生首先判断含参导数题的分类情况，根据具体题型制定困局破解方案，从而快速、准确求解。这既能为学生在日后含参导数题学习中增强自信心，又能让学生真正掌握含参导数题求解技巧。

参考文献：

[1]王丝丝，陈国华.高中数学中的含参问题及其解法[J].语数外学习：语文教育，2020（01）：35-37.

[2]李文东.利用导数解决含参不等式参数取值范围问题的策略[J].中学数学研究（华南师范大学）：上半月，2020（4）：12-14.

[3]张雷.导数法在高中数学解题中的有效应用[J].教育研究（2630-4686），2019（3）：54-55.

四川省成都外国语学校 四川省成都市 614000