浅谈北师版小学数学教材“图形与几何”领域的转化思想
崔毅



摘 要:一堂课所包含的内容应该有两条线,明线和暗线.明线就是数学知识,暗线是数学思想方法.数学思想是系统学习数学知识之后所提炼出来的隐藏在知识背后的技能,因此授课时教师不仅要关注显性的数学知识的传授,更要注重隐形的数学思想的渗透.那么,北师大版教材在“图形与几何”领域是如何渗透“转化思想”的呢?下文从图形认识、度量、计算、公式推导等几个方面阐述,北师版小学数学教材是如何在“图形与几何”领域渗透转化思想的.
关键词:图形与几何;转化思想
中图分类号:G622文献标识码:A文章编号:1008-0333(2020)17-0053-02
转化思想是数学的基本思想之一,对于转化思想的掌握,需要一个潜移默化的过程,它是长期的、逐步积累的.一堂课所包含的内容应该有两条线,明线和暗线.明线就是数学知识,暗线是数学思想方法.数学思想反映着数学各部分知识之间的联系,是系统学习数学知识之后所提炼出来的隐藏在知识背后的技能,因此授课时教师不仅要关注显性的数学知识的传授,更要注重隐形的数学思想的渗透.那么,北师大版教材是如何渗透“转化思想”的呢?
说到“转化思想”,可以想到许多的历史故事.例如三国时期的曹冲称象,将大象的体重转化成了许多石块的重量;例如伟大的物理学家爱迪生,有一次将一只灯泡交给了阿普顿,要求他计算出灯泡的体积,阿普顿通过画图、复杂的测量和计算,才得出了灯泡的体积,而爱迪生就是在灯泡里装满水,再把水倒进量杯,就量出了灯泡的体积.这些都是典型的“转化思想”,也是数学家独特的思维方式.
“转化思想”要求我们在解决有关数学问题时,能够运用观察、分析、对比等多种恰当的方法,将未知转化为已知,将复杂转化为简单,将抽象转化为具体等,使问题能够得到更好的解决.转化思想是数学的基本思想之一,对于转化思想的掌握,需要一个潜移默化的过程,它是长期的、逐步积累的.
一堂课所包含的内容应该有两条线,明线和暗线.明线就是数学知识,暗线是数学思想方法.数学思想反映着数学各部分知识之间的联系,是系统学习数学知识之后所提炼出来的隐藏在知识背后的技能,因此授课时教师不仅要关注显性的数学知识的传授,更要注重隐形的数学思想的渗透.那么,北师大版教材是如何渗透“转化思想”的呢?
一、在图形认识中渗透“转化思想”
三年级上册《看一看(二)》一课(如图1),教材呈现了杯子与牙膏盒的两幅直观图,让学生判断这两幅图分别是谁看到的.目的是使学生初步体会从不同的角度观察两个物体,看到的两个物体的相互位置是不同的.有些学生将“空间相对位置”转化成了“平面图形相对位置”,上图是牙膏盒在左边,下图是牙膏盒在右边.将三维转化成二维,巧妙地将复杂的空间位置关系转化为更简单的空间位置关系.
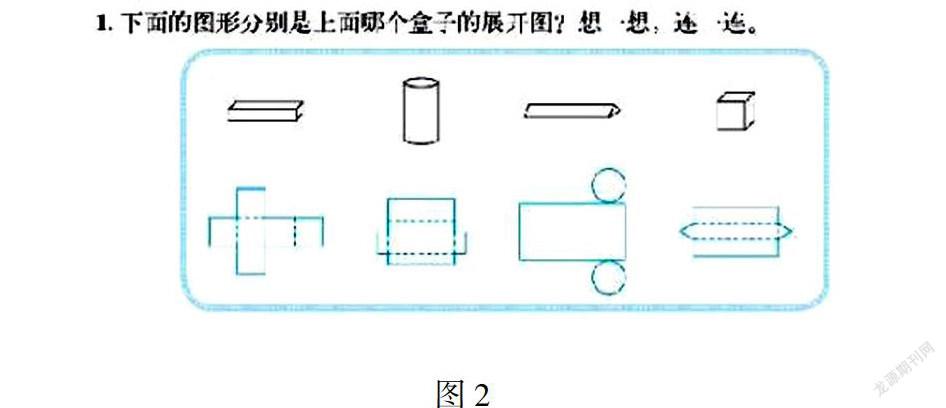
五年级下册《展开与折叠》一课(如图2),在练一练中呈现了长方体、圆图2柱、三棱柱、正方体的立体图形和平面展开图,要求学生将立体图形和平面图形对应.学生通过剪一剪、折一折的活动,能进一步了解到沿着不同的方式将立体图形展开,得到的图形是不一样的结论.这一活动能够加深理解“立体图形和平面图形之间是可以相互转化的”,发展了学生的空间观念.
六年级上册《搭积木比赛》,教材要求有两个方面.一方面是要求学生能正确辨认从不同方向观察到的立体的形状,并能画出相应的平面图形.另一方面是能根据从正面、左面、上面观察到的平面图形还原立体图形,进一步体会从三个方向观察就可以确定立体图形的形状,并能确定搭成立体图形所需要的正方体的数量范围.一方面是从立体图形到平面图形,将观察到的立体图形转化成三个平面图形,另一方面是从三个平面图形转化成立体图形.转化中渗透着联系,使学生在感知转化的过程中进一步体会立体图形与平面图形之间的联系.
二、在度量中渗透“转化思想”
图3四年级下册《探索与发现:三角形内角和》一课(如图3),教材要求学生能够探索和发现三角形的内角和等于180°,学生能够想出许多的办法,较容易的是测量三个角的度数之后相加,能够得到一个近似数,但还不足以说明三角形的内角和就是108°.聪明的孩子想到了剪拼的方法,将三个角剪下,拼在一起后得到一个平角,说明三角形的内角和等于180°,此方法巧妙地将三个角转化成了一个平角,具有较高的说服力.还有一些同学通过将三个角折在一起,拼成了平角,说明问题.个别同学将内角和转化为蚂蚁前进一周,三次旋转后回到初始状态,来说明内角和等于180°,更是巧妙.本课充分地激发了学生灵活运用“转化思想”探索三角形内角和能力,使“转化思想”得到了淋漓尽致地体现.图4
五年级下册《有趣的测量》一课(如图4),要求学生利用已有的生活、知识经验,测量出石块的体积.本节课在授课教师的引导下,三次渗透了转化思想.第一次,如何测量不规则橡皮泥的体积?可以将不规则的橡皮泥转化成长方体,通过测量长、宽、高计算出橡皮泥的体积.第二次,如何测量石块的体积?可以将石块转化成上升的水的体积、下降的水的体积、溢出的水的体积或者是上升部分水的体积加上溢出部分水的体积.在这两次转化中,学生能深刻地体会到,虽然转化的方式有所不同,但方法都是一样的,都是将不规则的形状转化为规则的形状.第三次转化,如何测量一粒黄豆的体积?由于一粒黄豆体积太小,不易观察和测量,因此转化为测量100粒黄豆的体积,再除以100得出一粒黄豆的体积.而三次的转化,都可以归结为将“未知”转化为“已知”,这是数学上常用的基本方法,在本节课得到了很好地渗透.
三、在计算、推导中渗透转化思想.
五年级上册《多边形面积》一单元.一项重要任务是探索平行四边形、三角形、梯形的面积公式.教材提供的基本方法正是“转化”的方法.在探索平行四边形面积公式前,学生只掌握了长方形和正方形面积计算公式,因此,平行四边形只能转化为长方形.在探索三角形面积公式时,因为已经掌握了平行四边形的面积公式,因此可以将三角形的面积转化为平行四边形或长方形.而在探索梯形面积公式时,学生能够根据学习经验,将梯形转化为平行四边形、两个三角形或三角形加平行四边形等方法解决.在本单元的复习课中,教师可再次唤起学生关于几种图形之间的联系,学生能够发现,原来三角形、长方形、平行四边形、梯形之间都是可以互相转化的,也体会到了数学知识之间的联系.数学知识并不是独立的、分割的,它们之间有着千丝万缕的联系,只要我们用心观察,就会发现更多的联系,数学世界就是这么的奇妙.
在五年级上册《组合图形》一单元中,进一步通过分割、添补、移补等方法,将组合图形的面积转化成了基本图形的面积计算.进一步使学生体会到了“转化思想”的重要性.
总之,数学思想的学习过程是一个漫长的、逐步积累的、不间断的过程.认真研读北师版教材,涉及到“转化思想”的内容丰富且精彩.教材在转化思想的渗透上根据知识的先后顺序、知识的难易程度、不间断地做了合理的渗透.从学习长方形、正方形,到学习平行四边形、三角形、梯形,再到后来的圆柱等等.在这一循序渐进地过程中,潜移默化地渗透着“转化思想”,使学生能够在不知不觉间掌握这个方法来分析问题、解决问题.这无形中提升了学生分析问题和解决问题的能力.转化思想就像一根无形的锁链,将零散的知识点巧妙地联系起来,使转化思想成为学生解决问题的有利策略.
参考文献:
[1]陈小梅.转化思想在小学数学空间与图形教学中的运用[J].新课程(小学),2017(10):14.
[2]陶书敏.转化思想在小學数学图形与几何教学中的应用[J].中小学教学研究,2019(8):35-36.
[责任编辑:李 璟]

