核心素养背景下初中数学图形微课教学探析
朱长青


[摘 要] 核心素养背景下,微课的渗入,改变了过去固有的教学模式,其通过演示几何动态,有效培养了学生直观想象的核心素养;通过创设生活情境,有效培养了学生数学建模的核心素养;通过借助类比思想,有效培养了学生逻辑推理的核心素养.
[关键词] 初中数学;核心素养;微课
核心素养背景下,微课的渗入,改变了过去固有的教学模式. 教学形式不再是一支粉笔、一块黑板、一堂课. 传统的数学课堂教学,学生只是一味地接受教育,课堂没有生机与活力,教学效果可想而知. 微课致力于提高学生的参与程度,深刻剖析每一个知识点,运用现代教育技术手段达到了优化整合教学资源的目的,尤其在数学的图形教学中更能发挥它的最大功效. 笔者以数学图形教学为例,深刻剖析微课在培养学生核心素养过程中的作用,以供参考.
演示几何动态,培养学生直观想象的核心素养
核心素养是课程改革深化、素质教育落地的核心要素. 直观想象是核心素养之一,也是有效课堂教学中一项重要指标,其包括直观感知与空间想象两种数学素养,要求学生能够借助空间想象去感知几何图形的形状、大小与相互位置关系等,达到对几何图形的理解,从而解决实际问题. 在日常课堂教学中,教师可以利用微课的演示功能,让几何图形在视频里动起来,让学生通过直观感受来探索数学问题的本质特征,在激发学生对数学学习的兴趣,提高学生对数学知识的理解的同时,培养了学生直观想象的核心素养.
例如,学生通过中位线定理,已经知道,连接任意四边形四边中点所得的四边形是平行四边形,那么连接矩形、菱形、正方形等特殊四边形四边中点所得的四边形是什么样的四边形呢?对此,学生总是存在混淆. 再者,将这些命题反过来,即它们的逆命题正确吗?学生一时语塞,如何让中点四边形的形象在学生心中留下深刻印象呢?笔者借助微课做了如下演示:
步骤一:在中点条件不变的情况下,让四边形分别变形为矩形、菱形、正方形、等腰梯形,看它们的中点四边形是什么四边形,如图1、图2、图3、图4、图5所示.
通过这个演示,学生可以直观地感知矩形的中点四边形是菱形,菱形的中点四边形是矩形,正方形的中点四边形是正方形,等腰梯形的中点四边形是菱形.
步骤二:那么将上述几个命题反过来,它们的逆命题成立吗?即中点四边形是菱形的四边形是否一定是矩形或等腰梯形呢?中点四边形是矩形的四边形是否一定是菱形呢?中点四边形是正方形的四边形是否一定是正方形呢?通过微课的演示,如图6、图7、图8所示.
學生直观地得到,中点四边形是菱形的四边形只需要满足一个条件,即对角线相等;中点四边形是矩形的四边形只需要满足一个条件,即对角线互相垂直;中点四边形是正方形的四边形只需要满足两个条件,即对角线互相垂直且相等.
整个教学过程,微课发挥了重要作用,它将图形动起来,演示了在纸面上无法演示的无数种情况. 如让一个四边形的对角线相等,然后看它的中点四边形是什么四边形,在保证对角线相等的情况下,微课中的几何画板演示了无数种情况,以不可辩驳的事实,使学生认为只要对角线相等的四边形,它的中点四边形就是菱形,进而激发了学生的求知欲望,提高了学生课堂教学的参与度量,培养了学生直观想象的核心素养.
创设生活情境,培养学生数学建模的核心素养
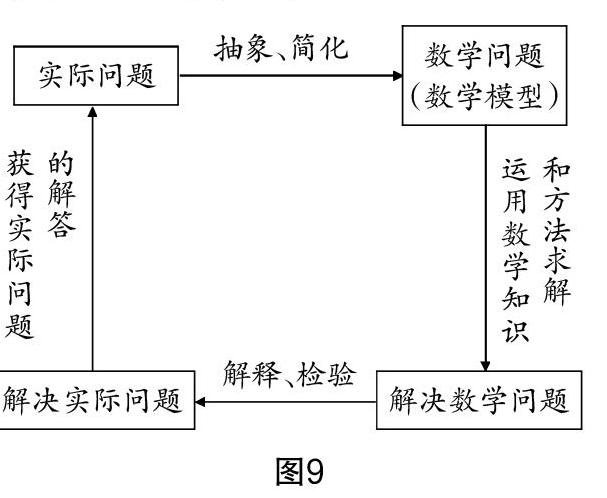
特级教师张思明提出,我们通过数学建模的教与学要为学生创设一个学数学、用数学的环境,为学生提供自主学习、自主探索、自主提出问题、自主解决问题的机会. 新课程标准中对数学建模的描述为,对实际生活问题进行抽象,把实际问题抽象为一个数学问题,然后用数学的语言、数学知识和方法进行构建,通过数学问题的解决从而解决实际问题的过程.它的流程图如图9所示. 可见,数学建模的过程可以培养学生应用数学的能力,培养学生的创造力. 在教学中,教师通过微课为学生创设一个学数学、用数学的生活情境,唤起学生的有意注意,吸引学生参与到课堂教学中,让学生参与到发现、提出问题,探索、解决问题的全过程.
例如,在轴对称与轴对称图形教学中,为了使学生对轴对称有切实的生活体验,微课视频创设了这样的生活情境:如图10所示,它包括剪纸中的轴对称图案、蝴蝶、飞机、水中的倒影.通过生活情境的展示,学生感受到轴对称图形是指把这个图形沿一条直线对折后,直线两旁的部分能互相重合,建立了轴对称的数学模型.
又如,在图形的平移教学中,为了使学生对平移有切实的生活体验,能从实际生活情境中抽象出平移这样的数学概念,在微课视频中设置了这样的生活场景:如图11所示,它包括电动平移门、徐徐上升的国旗、通过平移拼成的图案、上升的电梯等.通过生活情境的展示,学生从中抽象出平移就是一个图形的直线运动,它由移动的方向与距离决定,建立了平移的数学模型.
借助类比思想,培养学生逻辑推理的核心素养
在空间与几何图形的学习中,逻辑推理起着至关重要的作用,其是指从已知条件出发,应用定义、定理、公理推出一个命题是正确或错误的过程,包括归纳推理与演绎推理两种形式,培养学生的逻辑推理素养,即是培养学生提出发现命题的能力,有理有据的说理能力,从而进一步理解数学知识之间的相互联系. 教学中,教师可通过微课,借助类比的方法,培养学生的逻辑推理能力,提高学生独立思考问题的水平.
例如,在学习圆内接四边形的性质时,如何证明圆内接四边形“对角互补”的性质呢?教学中,教师通过微课,先让学生回忆圆周角定理的证明过程,微课中呈现了三种情况,即圆心在圆周角的边上,在圆周角的内部,在圆周角的外部,如图12所示.然后,教师让学生类比圆心与圆周角的位置关系,猜测圆内接四边形与圆心可能有哪些几何关系,很快学生会画出圆内接四边形与圆心的三种位置关系,即圆心在圆内接四边形的边上、内部和外部,如图13所示.类比圆周角定理的证明过程,学生通过作圆的半径证明了三种圆内接四边形对角互补.微视频的呈现,勾起了学生的回忆,通过类比,发展了学生独立思考的能力,提高了学生逻辑思维的缜密性与科学性.
微课作为一种全新的教学手段,培养了学生直观想象、数学建模、逻辑推理的核心素养.实现了数学教学形式的多元化,广大数学教育工作者,应善于反思勇于开发,相信微课的价值与作用会得到更多的开发与利用.

