浅谈初中数学课堂动态生成的应对策略
王凤敏
[摘 要] 叶澜教授这样说过:“课堂应是向未知方向挺进的旅行. ”由此可见,动态生成会有许多意外和惊喜. 文章借鉴多个课例,详细记述了以下应对动态生成的教学策略:在“节外生枝”处因势利导,生成精彩;在“花繁叶茂”处及时捕捉,生成精彩;在“花絮飘扬”处借题发挥,生成精彩;在“事故”处华丽转身,生成精彩.
[关键词] 课堂教学;动态生成;意外
在新课程改革的推动下,数学课堂是开放的,教学过程则是动态生成的,灵动的课堂教学总是伴随着“不和谐的音符”. 而这些“不和谐的音符”往往会被一些教师视为过程推进中的“绊脚石”,或轻描淡写地应对,或视而不见地略过. 事实上,课堂中的意外往往伴随着学生的创造性思维,是促进动态生成的载体,值得教师用心去“摘取”.
那么,该如何处理课堂中的动态生成呢?笔者认为,教师需要有效把握教材,充分预设教学目标,准确捕捉关键性的“意外”,及时引导学生展开积极思考,将“意外”灵活运用到教学中,从而成为最有益的教学资源. 本文借鉴多个课例,讨论应对动态生成的策略.
在“节外生枝”处因势利导,生成精彩
教师在课前需要从学生的知识基础和生活经验出发,进行预案设计,力求学生快速进入课堂,产生求知欲望,进而自我感悟新知. 但问题是,很多时候教师精心预设了教学环节,但学生的反应却是始料未及的. 此时,教师需善于因势利导地及时调整教学方案,从学生的思维生长点延伸开去,任其展露,并利用好教学机智不着痕迹地因势利导,使其转化为有效的教学资源,演绎精彩课堂.
案例1?摇 已知一个四边形的四个内角之比为2 ∶ 5 ∶ 6 ∶ 7,则该四边形的四个外角之比为______.
不少学生在完成这一问题时,易快速形成7 ∶ 6 ∶ 5 ∶ 2的解答结果. 若此时教师仅仅认定其错误,并将正确结论和思路抛给学生,则会出现学生思维浅层化的现象,不利于学生的知识建构. 此时,教师可以从解答结果出发,因势利导,顺着学生的思路设计问题,通过串联式的问题让学生在探究中发现和修正错误,完善认知.
问题1:已知一个四边形的四个外角之比为7 ∶ 6 ∶ 5 ∶ 2,则该四边形的每个外角分别为多少度?
问题2:上述四边形中与外角相邻的内角分别为多少度?
问题3:已知一个四边形的四个外角之比为7 ∶ 6 ∶ 5 ∶ 2,则该四边形的四个内角之比是2 ∶ 5 ∶ 6 ∶ 7吗?
问题4:当一个四边形的四个内角之比为2 ∶ 5 ∶ 6 ∶ 7时,相应的四个外角之比为多少?并阐明原因.
以上案例中,教师充分尊重学生的认知倾向,以问题串为指引,让学生自然发现自身思维的偏差,并将其演绎为精彩的生成. 就这样,在“节外生枝”之时兼顾学生的思维,通过问题的形式让其深入思考,能让學生在思考和探究中达到完善认知的目的,能让课前预设在有意引导和无意生长之间不期而遇.
在“花繁叶茂”处及时捕捉,生成精彩
随着课堂教学的动态变化,教师需要将学生置于探究学习的核心地位,因学生而动,让学生不断地生成有效信息. 而面对“花繁叶茂”的精彩,还需要教师具有课堂应变能力,时刻关注、及时捕捉和灵活处理,从中优选出具有思维价值的问题,使其绽放出更多的课堂精彩■[1]. 如此,才能让课堂焕发勃勃生机,自然呈现优美的风景.
案例2?摇 以“分式方程”的教学为例.
问题:解分式方程■=■.
师:以上分式方程该如何求解呢?(学生一脸茫然,有的开始展开讨论)
师(拾级而上):一元一次方程的解法大家已经比较熟悉了,那么这个方程该如何求解呢?
生1:我们可以将其转化为一元一次方程.
师:是吗?那如何转化呢?
生1:去分母后求解,可解得x=3.
师:生1的答案正确吗?大家仔细观察,有何发现?
生2:当x=3时,原方程没有意义,所以该方程无解.
师:非常好!事实上,在解分式方程时,我们可以通过去分母将其转化为整式方程来求解,但检验这一步一定不能省略. (在总结期间,笔者发现生3似乎有不同的想法)
师:我发现似乎有同学此处有想法?(看向生3)
生3:我觉得可以先移项,得到■-■=0,再通分可得■=0. 这里要使得分式的值为0,则只需要分子等于0、分母不等于0即可. 由分子等于0可得x=3,而当x=3时分母等于0,所以原方程无解. (此时,学生都被生3的创意解法所震惊,教室里响起热烈的掌声)
案例2中,学生生成了课堂精彩. 教师在引导教学的过程中,关注学生,尊重学生,在亮点出现时及时发现并给予展示的机会,让学生当众介绍自己的探索过程,让全体学生也亲身经历一番,从而获得各自的体验. 这样的教学过程,不仅培养了学生的探究性思维,同时展示了教师对学生的尊重和教师的教学机智.
在“花絮飘扬”处借题发挥,生成精彩
课堂不应是预设的僵化程序,而应是教与学的融合,是师与生、生与生之间交流互动的动态过程. 在这个过程中,教师需要具备敏锐的观察力,想学生所想,思学生所思,及时捕捉学生思维生长的时机,在其思维“花絮飘扬”之处借题发挥,并为学生预留出充足的时空,让思维的花絮转化为有助于课堂生成的素材,使课堂演绎更多精彩,提升教学的实效性■[2].
案例3?摇 以“一元二次方程”的复习为例.
问题:解一元二次方程x2+2x-35=0.
这一问题的难度不大,不少学生很快便给出了一般性的解题思路,并求解. 教师在来回巡视的过程中发现,有一名学生给出了不同的解法.
师:下面请一名学生给大家展示一下他的解题思路.
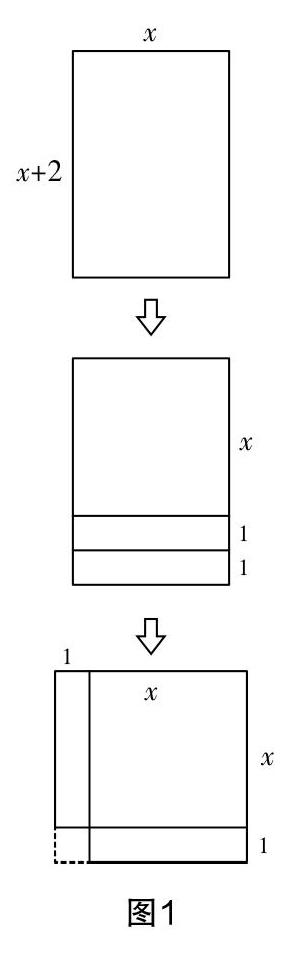
生1:首先将x2+2x-35=0变形为x2+2x=35,然后因式分解等式左侧,可得x(x+2)=35. 接着,可以将求解该方程的过程视为图1中一个长为(x+2),宽为x,面积为35的矩形剪拼为一个正方形的过程. 根据图1,原方程可转化为(x+1)2=35+1,即(x+1)2=36,则图1中x的值即为方程的正数解,而该方程还有一个负数解. 接下来此方程的变形结果则跟配方法相同.
师:非常新颖的思路!尽管整个解题过程较为复杂,但我们从其发散性思维中可以捕捉到一个重要的数学思想——数形结合……
学生的智慧源于深度数学思考,因为教师的借题发挥,使得师生的智慧发生了激烈的碰撞. 生1的讲解展示了一个不断思考和发现的过程,无论是生1还是其他同学都能从中享受到探究带来的兴奋,享受到发现带来的喜悦,这能让数学课堂因此有生命的色彩.
在“事故”处华丽转身,生成精彩
“施教之功,贵在引导,妙在点拨. ”错误是课堂教学中的一种正常现象,也是学生自己创造出来的宝贵教学资源,更是通向成功的阶梯. 因此,在学生出现错误时,教师需从“事故”着手,进行“柳暗花明”的点拨,让学生的思维“拨开云雾见明月”,让“事故”有华丽的转身,成为促进学生发展的宝贵资源,从而演绎为动人的“故事”,推动学生认知与思维的纵深发展,生成课堂精彩[3]■.
案例4 以“分式”的复习为例.
问题:化简■+■.
这是针对学生在化简分式过程中容易出现去分母这样的错误而设计的问题. 此问题一抛出,部分学生很快就落入“陷阱”,形成以下错误化简过程:
原式=(x+3)(x-2)+(2-x)
=x2+x-6+2-x
=x2-4.
师:以上化简过程正确吗?(学生从教师的提问中已然意识到化简過程有误,却没有找到错误的根源)
师(拾级而上):原式是等式还是代数式呢?
生1:我明白了,原式是一个代数式,所以不能直接去分母.
师:非常棒!那该如何解决呢?下面给大家一点时间自主探究和合作讨论. (学生进入思考和讨论状态,并很快生成结论)
生2:设A=■+■,因为x2-4≠0,所以可将A=■+■两边同时乘(x2-4),得到A(x2-4)=(x+3)(x-2)+(2-x),即A(x2-4)=x2-4. 所以A=■=1,即■+■=1.
师:非常棒的思路!
生3:我还有其他解法. 设A=■+■,则A=■-■. 因为x+2≠0,所以可将A=■-■两边同时乘(x+2),得到A(x+2)=x+3-1,即A(x+2)=x+2. 所以A=■=1,即■+■=1.
……
错误是学生最真实的暴露,教师理性地看待学生的错误,并辅以策略处理,可以让错误“美丽”起来. 案例4中,教师适时引导并合理铺垫,引导学生在纠错和改错中感悟道理和方法,则可以变错为宝,让“错误”成就精彩课堂.
总之,课堂是动态生成的,教师不能仅仅满足于教材的通透和充分的预设,还需要大胆因势利导、及时捕捉、借题发挥,通过及时的“放手”与有效的“收拢”,让课堂绽放光彩,从而最大限度地提高课堂效率.
参考文献:
[1]罗琳. 合理“预设” 激活“生成”——两个教学案例给予的启示[J]. 中国数学教育,2013(17).
[2]崔维春. 精心预设 有效生成——一堂精彩的数学活动课教学实录与反思[J]. 数学学习与研究,2015(10).
[3]任宏章. 预设促思 对话启智 生成发展——“从问题到方程(1)”课堂教学实录与反思[J]. 中学数学月刊,2017(02).

