“自主探究”何不尝试“教师搭台,学生唱戏”

◇ 江苏 褚红波

自主探究既是一种教育思想,又是一种学习方式.而自主探究是否高效,完全取决于教师的搭台水平,特别是有些内容上有深度、理解上有难度的课,更需要我们在怎么巧妙搭台这个问题上好好下功夫.在这些年的数学教学中,各个学校对课堂教学的方法改革方面有了一些有益的尝试,但是,从实际效果来看,自主探究这个环节做得并不好.有时候,自主探究变成了教师面对一些棘手问题的推脱,或者成了学生七嘴八舌的哄闹和争辩,最后什么有价值的思维过程或者结论都没有留下.教师搭好台,学生才能唱好戏.下面就几个例子谈谈笔者的思考.

1 搭台要承上启下

搭台要承上启下,要有严密的逻辑性和深刻的启发性,要分析与显化数学思维过程.根据教材的特点、教学的方法和学生的具体学情,把学生引入与问题有关的情境中,让学生通过观察,不断积累丰富的感性认识,让学生在实践感受中逐步认知、发展,乃至创造,学生的探索热情一旦被点燃,学生的学习效率就会成倍增长.

1)回顾旧知

函数f(x)在区间[x1,x2]上的平均变化率为_____；

结合图1,解释平均变化率的几何意义：____.

上一节刚学的内容是平均变化率,以这个开头不突兀,又起到了温故知新的效果!

2)展示未知

已知函数f(x)＝－x2＋1,分别计算f(x)在下列区间上的平均变化率.

①[1,1.1]；

②[1,1.01]；

③[1,1.001].

3)实践研究

已知函数f(x)＝x2.

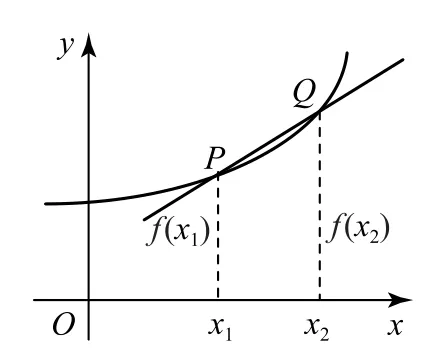
图1

(1)求函数在[1,1＋t]上的平均变化率；

(2)求函数在(1,f(1))处的切线斜率.

2 搭台要层层铺垫

搭台要“瞻前顾后”、层层铺垫,合理设计学生思维上的过渡和衔接.

线性规划中,学生理解的难点其实是目标函数的几何意义,所以教师要能及时发现这个问题,进行挖掘补充,弥补各知识之间的断层.

1)回顾旧知

①作出函数y＝x＋1,y＝2x＋1,y＝3x＋1,y＝－x＋1,y＝－2x＋1,y＝－3x＋1的图象；

②作出函数y＝x＋1,y＝x＋2,y＝x＋3,y＝x－1,y＝x－2,y＝x－3的图象.

由①可知,y＝kx＋1,k 是直线的____；

k＞0时,直线____,k 越大,直线____；

k＜0时,直线____,k 越小,直线____.

由②可知,y＝x＋b,b 是直线的____,这些直线有什么特点?

位置越靠上的,b 越____；位置越靠下的,b越____.

这几个问题很有必要,解决线性规划问题,必须解决斜率和截距的几何意义.

2)展示未知

一条直线方程为y＝kx＋1,经过点P(2,1)时斜率k＝____；

一条直线方程为y＝kx＋1,经过△ABC 区域,kmin＝____,kmax＝____；

一条直线方程为y＝x＋b,经过点p(3,2)时截距b＝____；

一条直线方程为y＝x＋b,经过△ABC 区域,bmin＝____,bmax＝____.

直线经过一点,截距或斜率有了确定的值,而线性规划是让直线经过了一个区域,从而截距或斜率有了范围,有了这样一个从点到面的过渡,学生理解起来就轻松多了.

3)实践研究

只要教师能将各个知识间的断点合理地搭建好,学生理解起来水到渠成,这样的探究不会让学生为难,并能感受到成就感.

3 搭台要实事求是

搭台要实事求是,不盲目拔高,重视剖析知识的形成和发展过程.例如让学生自主探究函数单调性定义时,引导学生从形入手,直观感知.

1)回顾旧知

请同学观察下面两组在相应区间上的函数,然后指出这两组函数之间在性质上的主要区别是什么.(一组增函数,一组减函数)

2)展示未知

结合总结的规律来观察图2——某城市某日24小时气温变化图.

图2

在区间[4,14]上,θ 随t 的增大而增大,这一特征用数学符号来刻画,该如何表述呢?

a)取t1＝4,t2＝14,得到相对应的θ1,θ2,有θ1＜θ2,所以在[4,14]上,θ 随t的增大而增大；

b)取t1＝5,t2＝6,t3＝8,t4＝10,得到相对应的θ1,θ2,θ3,θ4,有θ1＜θ2＜θ3＜θ4,所以在[4,14]上,θ随t的增大而增大；

c)取该子区间内所有的值t1,t2,t3,…,tn,得到相对应的θ1,θ2,θ3,…,θn,有θ1＜θ2＜θ3＜…＜θn,所以在区间[4,14]上,θ 随t的增大而增大.

3)实践研究

在区间[4,14]内任意取两个值t1,t2,当t1＜t2时,都有θ1＜θ2,是否可以说θ 随t的增大而增大?

通过一系列的设问,使学生处于积极思考的状态,从具体到抽象,通过实例使学生加深对定义的理解,与其不切实际地期待学生一口气“研究”出正确的结果,不如实实在在引导学生探索.自主探究不只是学生的探究,也是教师探究教学规律,创造新形式、新方法,多积累怎么把台子搭建好的过程.