探究新课程教学中运算能力的培养

◇ 陕西 程金林

数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析是高中数学核心素养的六个方面,其中数学运算能力是学习数学的基础.欲培养学生数学运算能力,需要教师在教学过程中向学生讲解在数学运算过程中常犯的错误,避免学生犯相似的错误,在课堂教学过程中潜移默化地培养学生运算能力.

1 深度理解运算的本质

在高中阶段的学习中,学生会发现数学运算能力与初中有不同的要求.初中阶段的运算能力主要考查数的计算和方程的求解等,而高中会涉及一些抽象的运算,例如,在高中阶段,学生会学习集合,集合的运算相对于他们以前学过的加减乘除运算来说就是一种抽象的运算.

分析计算此类问题时,学生会发现集合的运算不像加减乘除的计算那样简单、直接,进行两个集合的运算时,学生首先要掌握集合运算的本质,并对运算的本质有深刻理解.

教师讲解这部分内容时,应该注重对定义的讲解,因为学生之前未接触过此类概念,所以比较陌生,掌握起来比较困难,从课本定义的角度来讲,A ∪B表示所有属于集合A 或者集合B 的元素组成的一个新集合,称为集合A 与B 的并集,记作：A∪B,读作“A 并B”.数学教师在讲解定义的时候一定要着重强调定义中“或者”一词.

对于此类概念的讲解和集合的运算,数学教师还可以借助以下两种方法辅助学生理解.

1)集合语言描述法

A∪B＝{x|x∈A 或x∈B},运用集合语言描述的方法可以帮助学生将复杂的概念转化为简单、通俗易懂的数学语言,方便学生理解与掌握.

2)Venn图表示法

Venn图表示法是指将集合的运算通过Venn图(如图1)的方式简单明了地加以表示,避免学生在集合的运算过程中出现重复元素或者漏掉元素而导致做题错误.

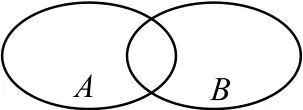
图1

例1利用Venn图表示法进行求解,如图2.

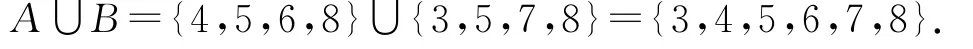
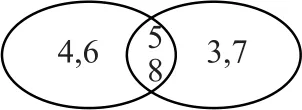
图2

通过集合语言描述法和Venn图表示法可以帮助学生加深对集合运算的概念的理解,并帮助学生使集合运算更加简单明确,避免出现错误,提高学生的运算能力.

2 加深对计算公式的记忆

在高中阶段的学习过程中,学生也会常常需要记忆一些公式,要避免在以后解题的过程中因为公式记忆不够熟练、模棱两可而导致计算出现错误.

例如,部分公式可以运用口诀法进行记忆.教师常向学生介绍的口诀为“奇变偶不变,符号看象限”和坐标平移公式“左＋右－”等.本文给出“奇变偶不变,符号看象限”的具体应用.

学生首先把α 看作一个锐角,口诀中讲的奇数和偶数主要看的是公式中的系数k.若系数k 是奇数则需要变函数名也就是正弦与余弦之间的变化；符号看象限是指将α 看成锐角的时候,α 在第一象限,进而推导所求的角在第几象限,判断对应三角函数的取值,确定其正负.

分析因为sin(－α)中的系数是1,由于1为奇数,所以要变名成为cosα,然后判断cosα 符号的正负,从口诀中知道符号的正负需要看象限.首先,把α 看成锐角时,α 在第一象限,从而知道－α 在第四象限,进而知道－α 这个角在第一象限,第一象限角的正弦值应该是正数,也就是sin(－α)的值是正数,所以等式右边的值应该也为正数,α 是被看成锐角,cosα 是正数,所以sin(－α)＝cosα.

学生运算能力的培养需要每一位学生在实践过程中不断积累经验,不断提高自己的运算能力,这就需要教师在向学生讲解基本运算技巧之后,让学生进行实践练习,丰富自己的经验,提高运算能力.