SINS辅助的星敏感器在线标定方法

谷 丛， 刘 洋， 吴成智， 肖 波， 林建华

（1.上海航天控制技术研究所，上海201109；2.上海惯性工程技术研究中心，上海201109）

0 引言

航天器姿态信息对于航天飞行任务至关重要,单纯地依靠某一种导航方式已不能满足航天器对姿态精度的要求。因此,通常采用将多种导航设备进行最优组合的方式来提高导航系统的精度［1］。由于捷联惯导系统（Strapdown Inertial Navigation System,SINS）与星敏感器均具有不向外辐射任何信息、抗干扰性强、隐蔽性好、完全自主等特点,SINS/星敏感器组合导航系统必将成为现代军事及民用领域内的一种重要导航系统。可以充分利用星敏感器的长期高精度定姿信息和SINS的短期高精度导航信息,通过Kalman滤波技术将它们有机结合起来构成组合导航系统,从而达到取长补短的目的［2-3］。但是在实际飞行任务中,星敏感器会受到发射时的振动和冲击、恶劣的太空工作环境等因素影响,其内部参数会相对于地面标定时发生较大变化,这将严重影响星敏感器的定姿精度。因此,必须对星敏感器的安装误差进行严格的在轨实时标定,其安装误差的实时标定与修正是确保星敏感器测量精度的关键［4-5］。

国外学者最先开始了对星敏感器在线标定技术的研究：Shuster等［6］研究了姿态敏感器相对和绝对准线安装误差的在轨标定；Crassidis等［7］研究了包括扩展Kalman滤波算法的三轴磁强计实时在轨标定方法；Pittelkau［8］提出了对准Kalman滤波算法用于陀螺和星敏感器的在轨标定,但模型复杂,计算量大。近年来,国内学者在姿态敏感器在轨标定方面也取得了较多研究成果［9-10］,但星敏感器在轨标定方法在算法实时性、模型效率和最优性以及误差源考虑等方面还值得进一步深入研究。为此,本文提出了一种SINS辅助的星敏感器在线标定方法。该方法不需要采用造价昂贵的高精度转台和模拟星光学设备等,只需飞行器在飞行过程中做简单的摇翼动作,即可对星敏感器的安装误差角进行实时在线标定,工程应用价值高。

1 星敏感器姿态输出

星敏感器测量坐标系c与载体坐标系b之间的姿态转换关系在星敏感器安装时可以确定。为方便起见,这里假设星敏感器测量坐标系c与载体坐标系b基本重合,仅存在残余安装误差角α=［αxαyαz］T（小角度）, 如图1所示, 则有

式（1）中,（α ×）为由α构成的反对称阵, 即。

图1 星敏感器坐标系与载体坐标系安装误差示意图Fig.1 Installation error diagram of star sensor and carrier coordinate system

由于星敏感器的测量精度很高,标定星敏感器的安装误差以后,星敏感器自身的测量误差vcns可以认为是零均值的白噪声。所以,实际星敏感器相对于惯性坐标系的输出为

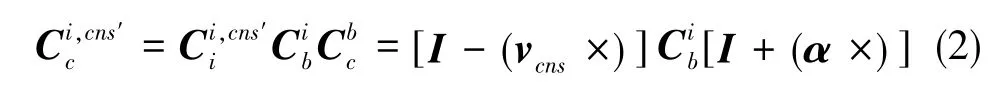
2 SINS姿态输出

式（3）中,np和nc分别为由计算姿态和计算位置确定的导航坐标系,设真实位置处的导航坐标系为nt, 则式（3）可展开为

代入式（4）,忽略高阶小项,整理可得

3 SINS/星敏感器组合导航状态方程

针对SINS系统,假设惯性器件的其他误差项已得到很好的校正,只考虑其姿态误差φn、速度误差δvn、位置误差δpn、陀螺随机常值漂移εb以及加速度计随机常值误差Δb。对于星敏感器,仅考虑其安装误差角α。 因此,SINS/星敏感器组合导航系统的状态向量x为状态方程为

式（7）中,ω为陀螺输出的角度信息,f为加速度计输出的比力信息,其余相关矩阵分别为

式（8）中,RMh为子午圈曲率半径,RNh为卯酉圈曲率半径。

4 SINS/星敏感器组合导航系统量测方程

根据叉乘反对称矩阵特性,从式（9）中提取量测量

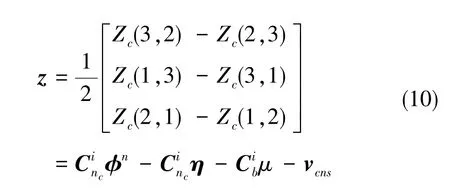
可得量测方程为

当飞行器角运动使星敏感器安装误差角充分可观测后,极限估计精度与星敏感器的精度相当。

5 仿真验证

5.1 惯性器件参数设置

试验系统采用光纤捷联惯导,陀螺常值漂移为 0.05（°）/h, 角随机游走系数为 0.008（°）/h1/2,刻度系数误差为1×10-4；加速度计常值偏置为4×10-5g,速度随机游走为1×10-5g·s1/2,刻度系数误差为1×10-4。 设惯导姿态初始误差为［30′ 30′30′］T,星敏感器和惯导间的安装误差角为［10′ 20′ 30′］T,星敏感器精度如表1所示。

表1 星敏感器精度Table 1 Accuracy of star sensor

5.2 飞行器轨道设置

将飞行器轨道高度h设置为400km,地球半径Re=6378160m,得轨道半径R为

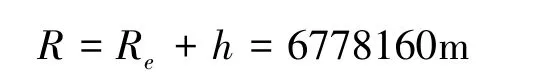
飞行器的飞行速度v、角速率ωr、向心加速度ac分别为

设轨道的升交点赤经Ω=20°,轨道倾角φ=40°。

设轨道的初始角位置θ0=60°, 即初始位置为

5.3 飞行器机动结果

（1）机动角速率的影响

设飞行器从10s开始机动,先绕横滚轴角机动80s,往复摇翼一次,休息60s,再绕航向轴角机动80s,此后绕轨道匀速飞行。根据表1,设角速率分别为 0.1（°）/s、 0.6（°）/s、 1（°）/s 三个等级,易知三个等级中的摇翼幅度分别为2°、12°和20°。惯导姿态角和星敏感器与惯导间的安装误差角曲线分别如图2和图3所示。

图2 不同角速率下惯导姿态角Fig.2 Attitude angles of SINS under different angular velocities

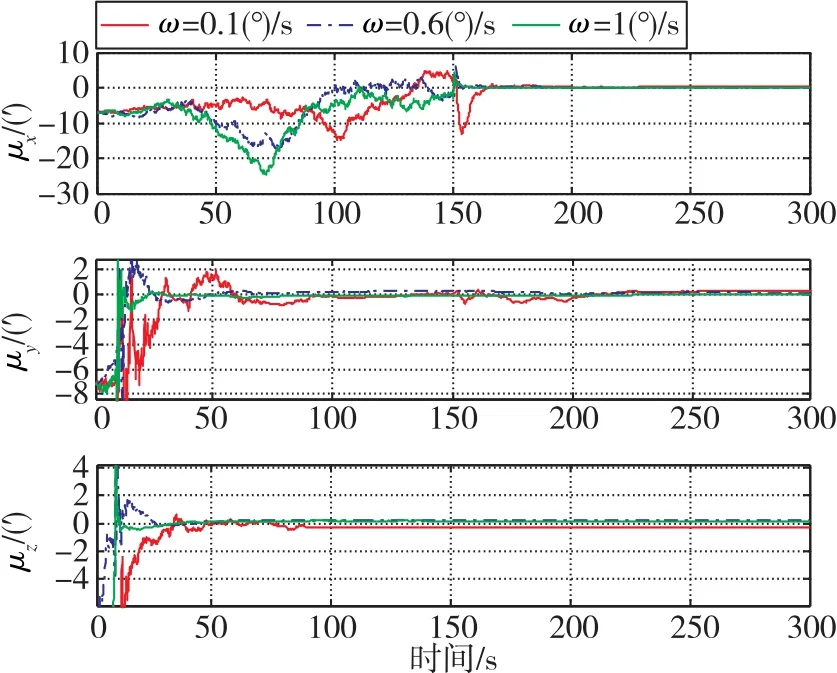
图3 不同角速率下星敏感器与惯导间的安装误差角Fig.3 Installation error angles between SINS and star sensor under different angular velocities

由图2和图3可知,飞行器10s开始绕横滚轴x机动时,俯仰轴y和航向轴z的星敏感器与惯导间的安装角迅速得到估计；150s后绕航向轴z进行角机动后,方能估计出横滚轴x的安装误差角。相同机动时间,角速率越大,即摇翼幅度越大,惯导姿态角和星敏感器与惯导间的安装误差角收敛速度越快。仿真结束时刻,星敏感器与惯导间的安装误差角约为 0.1′（角速率为 0.6（°）/s 和 1（°）/s）和 0.4′（角速率为0.1（°）/s）,即摇翼幅值越大,收敛精度越高,安装误差的总体估计率达到95%以上。

（2）机动时间的影响

飞行器从10s开始以0.6（°）/s的角速率绕横滚轴x往复摇翼一次,完成一次摇翼的时间分别为80s、 160s、 240s, 即摇翼幅度分别为 12°、 24°和48°三个等级。惯导姿态角和星敏感器与惯导间的安装误差角曲线分别如图4和图5所示。

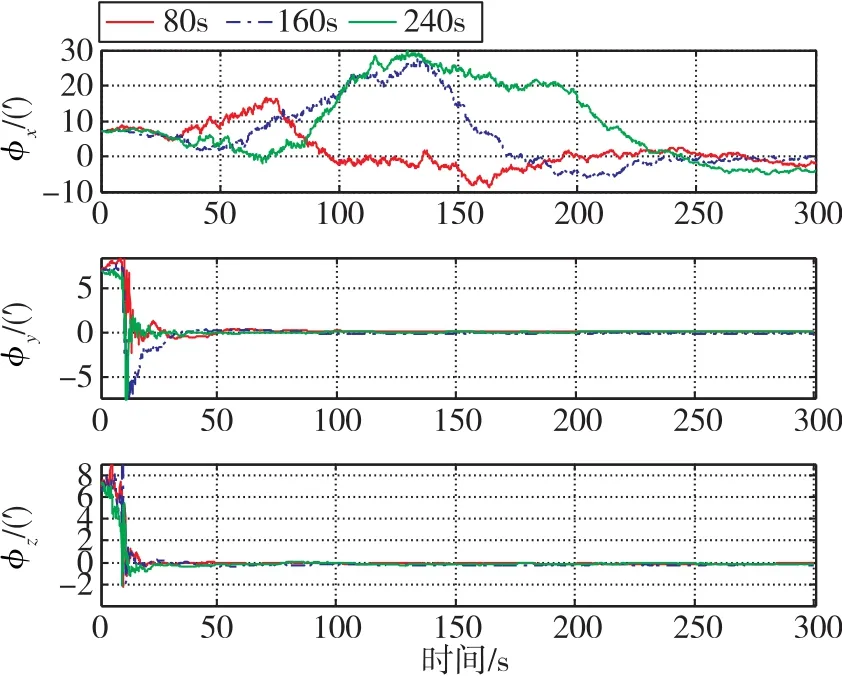
图4 不同摇翼时间下的惯导姿态角Fig.4 Attitude angles of SINS under different wing times

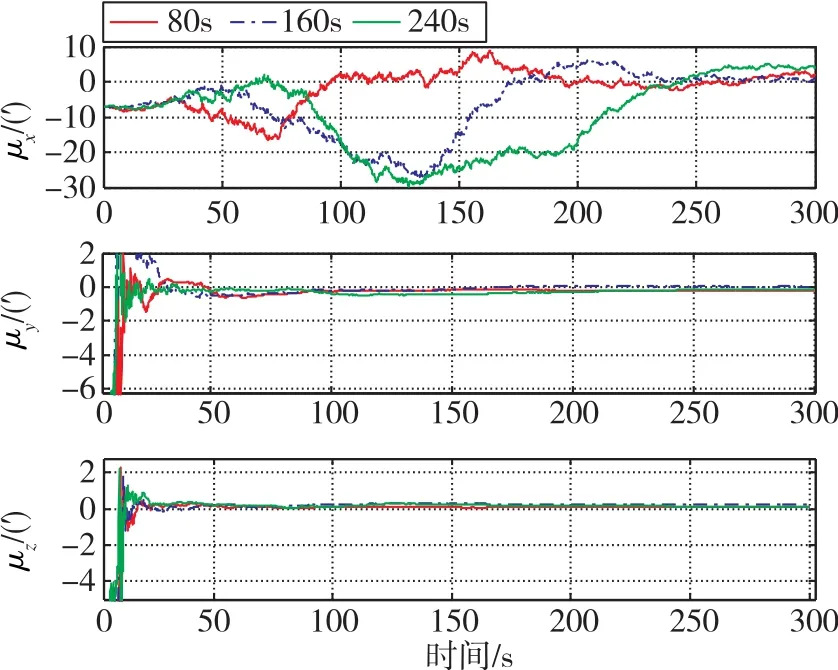
图5 不同摇翼时间下的星敏感器与惯导间的安装误差角Fig.5 Installation error angles between SINS and star sensor under different wing times

由图4和图5可知,飞行器10s开始绕横滚轴x机动时,x轴的星敏感器与惯导间的安装角无法得到估计；进一步验证了若估计出三个轴向的星敏感器安装误差角,飞行器必须进行至少两个轴向的角机动。飞行器以相同角速率进行机动时,机动时间越长,幅值越大,惯导姿态角和星敏感器与惯导间的安装误差角收敛速度越快,精度越高。

6 结论

本文研究了航天器在飞行过程中如何利用SINS对星敏感器和惯导间的安装误差角进行标定的方法。将SINS/星敏感器输出的姿态信息进行配准,构建了SINS/星敏感器组合导航系统的Kalman滤波模型,并对算法进行了数学仿真。利用本文提供的在线标定方法,飞行器在进行两个轴向的角机动后,星敏感器和惯导间的安装误差角可迅速得到估计,收敛速度和估计精度与飞行器机动幅值相关。针对不同角速率对应的星敏感器精度不同,应选择合适的角速率尽量延长机动时间,快速精确估计出星敏感器的安装误差角。本方法有效保证了星敏感器的定姿精度,具有良好的理论研究与工程应用价值。