基于极限学习机的黑障区智能导航算法

景羿铭，王 融，熊 智，赵 耀，刘建业

（南京航空航天大学自动化学院，南京211106）

0 引言

空天飞行器高速再入大气层时,存在黑障区通信中断的情况。而单独的惯性导航元件存在误差累计的缺点,若无辅助导航系统修正,惯性导航系统（Inertial Navigation System,INS）的精度会随着时间而下降［1-2］。当辅助导航系统信号具备可用性时,通过信息融合可以进行导航信息的误差修正。而在黑障区,即信号中断期间,此时飞行器速度仍然较快,不断的误差累计不仅会对飞行器的飞行安全造成威胁,也会增加飞行器出黑障区后的捕捉难度以及着陆的不确定性。同时,跳跃式返回的飞行器会两次进入黑障区［3］,这对导航系统的可靠性提出了更严格的要求。为保证导航系统在黑障区的可靠性,文献［4］针对黑障区通信失效的问题,根据头重尾弱的特点,在飞行器头尾分别安装两个全球定位系统（Global Positioning System,GPS）天线,以此测量姿态并进行修正,但该方法并无可靠的实际证明。为此,考虑在进入黑障区前,利用星敏感器对姿态信息进行修正以保证姿态的精确性,防止黑障区导航信息的过分发散。文献［5］针对黑障等恶劣情况设计了一种快速补偿的修正算法,但该算法仅在较短时间内有较好的效果。文献［6］提出了一种基于径向基函数（Radial Basis Function,RBF）神经网络预测的误差反馈校正方法,在GPS信号中断时用训练好的神经网络预测导航误差并进行修正,但RBF神经网络仍是反馈型神经网络,无法满足飞行器高速返回时的实时性。而极限学习机（Extreme Learning Machine,ELM）具备动态记忆且只有一层隐藏层,学习速度快,泛化能力强,可用于快速学习。ELM在许多领域都有应用,已成功用于低分辨率至高分辨率图像的转化,也可实现对蛋白质交互作用的预测,因其良好的泛化能力已成功应用于对日河流径流量、风速和干旱指数的预测［7-10］。该机器学习算法适合在需要高实时性的空天飞行器中使用,通过学习正常工作时的GPS数据,在GPS失锁时对惯性导航系统进行误差修正。

本文针对空天飞行器在黑障区失锁的问题,提出了一种基于极限学习机的黑障区智能导航算法。该算法利用ELM对GPS数据进行训练,在GPS失锁时仍可提供辅助导航信息。相比于传统的神经网络,该算法具有学习速度快、实时性高的优点,保证了飞行器在高速返回时导航系统的可靠性。

1 极限学习机原理

极限学习机是黄广斌等基于单隐藏层前馈神经网络提出的一种新的机器学习算法,可用于一般单隐藏层的前馈神经网络,其中的结点不一定是像神经元的结点［11］,其结构示意图如图1所示。

图1 极限学习机神经元示意图Fig.1 Schematic diagram of extreme learning machine neurons

给定具有M个隐层结点的极限学习机模型,其输出函数定义为

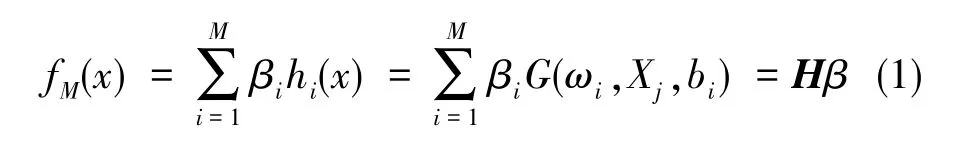
式（1）中,G（·）为激活函数；ωi为输入层与隐藏层之间的连接权重,bi为隐藏层的阈值,是随机选取且预先设定的参数；βi为输出层与隐藏层之间的连接权重,该值不需要迭代调整。与BP神经网 络 （Back Propagation Neural Network,BPNN）、RBF神经网络（Radial Basis Function Neural Network,RBFNN）的输出函数相比,ELM输出函数的参数均不需要反馈修正,这大幅提高了学习与计算效率。而H为输入样本情况下隐藏层的输出矢量,实际上将N维的输入样本映射到M维的ELM特征空间。

与反馈式神经网络不同,极限学习机算法只要激活函数能够满足无穷可微的条件,则预设参数可以不进行迭代调整。为符合计算习惯与计算机语言,对式（1）进行矢量化,那么对于固定输入的隐藏层参数来说,训练极限学习机就等价于求取线性系统Hβ=T的最小二乘值,即

为了能够具备良好的泛化性能,既要使极限学习机达到最小的训练误差,又要使其具有最小的输出权重方差。因此,极小范数解准则满足

由文献［11］可知,当隐层神经元个数与训练样本个数一致时,可直接求逆。然而在大多数情况下,隐层神经元个数是远小于训练样本个数的,这时需要利用损失函数求解最小值

式（4）中,H+为隐层响应矩阵H的Moore-Penrose增广逆。在极限学习机中,通常选择正交法对H+进行计算：

1）HTH非奇异时,HH+=（HTH）-1HT；

2）HHT非奇异时,H+=HT（HHT）-1。

2 基于ELM的黑障区智能导航算法

需要穿过黑障区的飞行器通常均是超高速飞行器,这类飞行器本身对导航系统的可靠性要求就极高,黑障区的长时间无修正飞行给飞行器的再次捕捉与安全着陆都带来了很大的风险。因此,本文提出一种基于极限学习机的黑障区智能导航算法,在GPS正常工作的时候利用极限学习机进行快速学习,当GPS修正时利用极限学习机回归预测辅助进行惯性导航系统的误差修正,保证黑障区导航系统的可靠性。

2.1 天文导航系统修正姿态误差

天文导航系统（Celestial Navigation System,CNS）独立工作,星敏感器敏感天体方位信息,测得的姿态信息精度高且误差不随时间累积。但是,星敏感器测得的姿态信息是载体系相对于地心惯性系的数据,该数据需要进行坐标转换为需要的导航坐标系下的姿态信息,转换过程中会引入计算误差,同时也会耦合到位置误差,故导致了天文导航系统可靠性的下降［12］。又因为天文导航系统在大气层内易受天气的影响,且进入黑障区后工作条件难以满足,所以为保证导航系统的可靠性,在进入黑障区前利用天文导航信息对陀螺输出信息进行开环修正,不影响GPS的闭环系统工作,其整体设计方案如图2所示。陀螺的误差估计修正要根据陀螺的原始输出信息解出载体相对于惯性坐标系的姿态信息,同天文定姿量测信息相结合,经由Kalman滤波器对陀螺的漂移误差进行估计和跟踪,为黑障区的导航系统可靠性提供保证。

图2 基于陀螺误差估计修正的导航系统方案示意图Fig.2 Schematic diagram of navigation system scheme based on gyroscope error estimation and correction

为有效利用高精度天文定姿信息,首先需要推导建立地心惯性坐标系下的系统状态方程。记载体相对于地心惯性坐标系的真实姿态四元数为Q,则

对式（6）求导, 可得

根据四元数运动学微分方程,可得载体真实姿态四元数微分方程和估计四元数的微分方程,分别为

将式（6）、 式（8）、 式（9）代入式（7）, 根据四元数运算规则,化简可得

根据四元数乘法运算规律及在姿态误差为小量的情况下,误差四元数δQ可近似为［13］

式（11）中,δq13为误差四元数矢量部分。

将式（11）代入式（10）, 忽略二阶小量, 同时对其进行线性化,可得

则状态变量定义如下

结合式（12）、 式（13）, 可得

式（14）中,F（t）为系统状态系数矩阵,G（t）为系统噪声矩阵,W（t）为系统噪声。

2.2 基于ELM的智能导航系统设计

（1）GPS失锁下的组合导航系统设计

导航系统通过辅助导航系统对捷联惯导误差进行最优估计,并对其进行误差校正,通常选择GPS测量信号。当GPS失锁时,导航系统变为纯惯性导航模式,解算结果无法修正,导致误差累计甚至发散,造成严重后果。如果在GPS失锁时仍能提供Kalman滤波观测值,组合导航系统相当于 “正常工作”,能继续对惯性导航解算结果进行修正。

根据上述原由,选择ELM进行拟合学习非线性系统模型。该系统的工作状态有两种方式：1）GPS有效时的ELM网络训练方式；2）GPS失锁时的神经网络预测方式。当GPS正常工作时,系统如图3所示。利用传统的INS/GPS组合导航系统进行误差修正（实线部分）,同时ELM利用正常数据在线学习（虚线部分）。当GPS失锁时,系统如图4所示,由ELM预测的观测值继续进行误差修正。

图3 GPS正常工作时的导航系统方案示意图Fig.3 Schematic diagram of navigation system scheme when GPS works normally

图4 GPS失锁时的导航系统方案示意图Fig.4 Schematic diagram of navigation system scheme when GPS loses lock

本文选取ELM的待预测信息为Kalman滤波的量测值,即惯导解算输出的位置和速度信息与GPS接收机测量的位置和速度的差值,该量测值必然与惯导系统的解算结果有关系,而惯导解算的速度和位置信息由加速度计和陀螺的输出计算而来。因此,二者存在某种数学关系,可以作为输入输出关系进行处理。

（2）极限学习机的训练方法

在实时变化的系统中应用时,需要网络具有最新的系统特征,此时需要持续对样本集进行更新,以此保证网络的预测能力。而若一直将新的样本纳入,会导致计算量不断增加,造成计算复杂度爆炸,导致网络性能的降低。考虑到上述问题,选择合适的时间窗对数据量进行限制,保证训练样本数合理且具备最新的系统特征。

待系统工作稳定后,将IMU量测数据和GPS的位置数据与速度数据保存至ELM样本集中,达到一定数量时开始神经网络的训练。在下一时刻,将新的样本值加入到现有样本集中,并将样本集中距离当前时刻最远的样本删除,保证样本数量恒定且具备系统的最新特征。

（3）极限学习机的预测方法

当GPS失锁时,导航系统工作于如图4所示的工作方式下。此时,由极限学习机预测的输出值取代原先的观测值计算过程。令系统继续工作,正常对惯导系统进行误差修正,防止系统发散。

当GPS信息恢复可用时,极限学习机再次工作于训练模式,重新开始训练。

3 仿真测试

为较好地体现效果,本文模拟航天飞机再入段15km～120km阶段,黑障区为30km～80km阶段（时间间隔为39s～489s）。初始速度为7800m/s,逐渐减速至300m/s。

总仿真时间为1213s,惯导解算周期为0.02s,滤波周期为1s；陀螺常值漂移为0.1（°）/h,陀螺白噪声为 0.05（°）/h； 加速度计常值误差为0.0001g,加速度计白噪声为0.00005g；卫星导航定位误差为20m,速度误差为0.2m/s,再入段的三维航迹如图5所示。

图5 再入段的三维航迹图Fig.5 Three dimensional trajectory of re-entry section

为比较GPS失锁时ELM的工作情况,分别采用GPS失效不补偿与基于ELM的智能导航算法两种方法在上述航迹下进行仿真实验,误差曲线对比如图6～图8所示。未进行修正的惯性系统会因在黑障区长时间得不到修正,即使出黑障区后得到正确的GPS数据仍无法阻止其发散。为更清晰地比较两种不同滤波方法的收敛精度,取图6～图8中的误差数据进行RMS统计,其统计误差如表1所示。

图6 位置误差曲线Fig.6 Curves of position error

图7 速度误差曲线Fig.7 Curves of velocity error

图8 姿态误差曲线Fig.8 Curves of attitude error

表1 导航信息误差精度对比Table 1 Comparison of navigation information error accuracy

由图6～图8、表1可知,基于ELM的黑障区智能导航算法对于惯性系统有良好的收敛作用。传统算法随着仿真时间的增长,误差呈发散趋势,而基于ELM的黑障区智能导航算法能保证导航系统处于收敛状态,说明该算法对黑障区具有良好的估计和跟踪效果。

4 结论

神经网络有助于实时性与非线性强的模型学习,本文提出了先利用天文导航系统在进入黑障区前进行陀螺误差修正,之后采用基于ELM的智能导航算法实现GPS失效时的惯导解算误差修正。仿真结果表明,基于ELM的黑障区智能导航算法为保证黑障区导航系统的可靠性提供了一种新的有效方法,具备一定的工程应用价值。