第一人称视角地形轮廓草图的真实空间重建

曾 升，耿国华，邹林波，周明全

(西北大学 信息科学与技术学院，陕西 西安 710127)

1 引 言

二维图像重建三维模型一直是计算机视觉研究的热点问题，主要包括基于运动结构的多图建模算法(Structure From Motion,SFM)，和从单个视图(Shaded Volume Rendering,SVR)直接建立三维模型。其中单幅图像只能提供二维信息，立体建模中缺少一维信息，二维图像的三维解释是不适定的[1]，所以多数单图重建三维模型需要大量的先验知识，有不少深度学习重建的方法[2-6]。而二维草图仅描述轮廓，能获取的信息更少，但由于其易于表达用户意图，运用二维草图来记录和表达视觉信息广泛存在于艺术绘图、工程设计人员CAD建模及三维模型检索等领域，草图是用户构思设计的直观体现[7-9]。

三维地形的生成有经典的分形布朗运动模型方法[10]、实例纹理合成方法[11]、自适应网格方法等[12]，从草图重建三维地形的关键是在2D草图轮廓与三维地形的在对应视角下，在一致的轮廓约束下进行地形重建，针对不同的重建问题已有不少研究成果。Rusnell[13]描述了一种基于加权图中距离的地形合成方法，地形中要素的位置通过放置单个地形特征的生成器指定。Gain[14]的地形合成方法提供了一个草图界面，创建或修改包含各种复杂地形的景观的界面，但不仅需要用户绘制轮廓、脊线，还需要绘制山体平面投影的边界曲线。还有一些着重研究基于实例的纹理合成技术以显著提高地形的真实感的方法[15-16]。Passos[17]的方法只需绘制山脉的轮廓线，但需要花费时间寻找匹配现实世界的数字高程(Digital Tertain Model,DEM)来创建逼真的地形。Ariyan[18]建立曲线网格从而在2D中绘制曲线的层次结构，它可以通过指定曲线的基本轮廓来控制从山峰向外的山脊形状。Ketabchi[19]基于草图的工具来集成为常用的数据源，可以从DEM中创建广泛的景观，提高数字地球数据的质量。Becher[20]使用基于三维曲线的基本体来有效地建模突出物，它提供了完整的空间地形的艺术自由，甚至可以构造悬垂和洞穴。Talgorn[21]提出一种新的基于分形的GPU模型来解决实时约束地形生成问题。针对可见草图生成三维地形的研究几乎都关注在提高地形真实感，提升用户自由度设计，加快建模速度等方面，但对轮廓重建的地形的实际空间位置是否合理并未考虑，完全是自由设计，然而反映用户脑海中的地形草图真实空间建模更符合地形设计的目的，本文致力于手绘地形草图的真实空间重建。

由于地形草图缺失一维信息，本身并不能提供完全的三维信息，重建真实空间三维地形有两个明显的问题，一是草图中地形轮廓线真实深度无法确定，并且在第一人称视角下的二维图像中的同一条轮廓在三维空间中存在无数种走向可能；二是仅有轮廓信息，前后遮挡且并没有更多细节。问题一中需要获取图像的深度信息，基本上分为基于双目视觉和单目视觉的方法，赵祚喜等[22]提出一种基于直接线性变换的三维定位方法实现空间点的世界坐标测量，李云雷等[23]针对有遮挡区域、深孔及凹槽的物体，提出立体定向靶标的探针式多视场三维视觉测量系统，解决更精细重建的问题。于洋等[24]融合ROS SLAM的Gmapping算法，提出一种复合坐标定位系统精准计算室内物体。而单目视觉方法由于不具备对极几何的理论支持，目标测距并不容易实现，韩延祥[25]利用小孔成像原理，建立成像点与目标点映射关系，计算相机的外参和内参，并计算特征点与光心的距离实现基于特征点的单目视觉测距方法。还有许多基于深度学习的估计深度图方法[26-29]，需要大量深度图数据集的支持。而用深度相机获取深度则更注重研究减少位姿估计的误差以提升三维重建的效果[30]。本文研究的草图由于都是单一视图，深度的获取只适合于单目测距，然而草图中的存在前后遮挡的多目标地形轮廓，且轮廓线在三维空间中未必平行于草图平面，无法直接获取确定的绝对深度值，能够确定只有相对深度的约束关系。对于前后遮挡且并没有更多细节的问题，由于不存在确定性的信息，如何合理补全以完整三维模型的展示也是需要解决的问题。

本文立足于从第一人称角度绘制具有前后遮挡轮廓的地形草图，研究符合摄影几何规律的三维真实空间地形自动建模。首先根据轮廓线的遮挡关系进行约束条件设定，初始化状态设定为多条草图地形轮廓线平行于视点平面；然后根据小孔成像模型，建立前后遮挡轮廓线的相对深度约束关系，即并不是直接计算绝对深度，而是在初始化状态下限定深度层之间的关系约束；再建立高度图模型，将二维立面曲线转变为DEM数据的等高线图，以周向分形插值填补高程数据完成骨架高度图；对于地形不同走向但在二维平面上一致的的情况，以旋转映射的方式完成非刚性的旋转变形，再以曲面拟合完成数据的补全；最后加入柏林噪声以增加草图未提供的具体细节部分的随机性，完成三维模型的多样性展示。

2 手绘地形草图的真实空间重建方法

本文研究符合摄影几何规律的真实空间定位建模。在之前周蓬勃[31]的研究中，已搭建了B/S架构的交互式平台实现国画中三维山水场景的快速建模，交互式绘制山体轮廓线、地平线、走向线，从而生成圆台图元并叠加生成三维曲面，以高斯滤波半径控制曲面的光滑度。本文提出的方法在提取草图轮廓线的基础上生成地形曲面，符合近大远小的摄影几何规律。这项研究的目的是直接从二维草图生成三维模型，图1是本文第一人称视角下绘制2D地形草图的三维真实空间重建框架图。小孔成像模型建立的相对深度关系是保证重建三维地形模型具备真实空间位置的理论基础，根据草图有限信息进行初始化设定是实现缺失一维信息情况下进行三维空间计算的前提，多样性变换部分的旋转映射是解决轮廓线在三维空间中未必平行于视点平面的关键，柏林噪声的加入是丰富草图本身缺失细节信息而进行的处理。

图1 地形草图的真实空间重建框架图Fig.1 Real spatial reconstruction frame of silhouettes sketch

2.1 初始化设定

尽管二维草图缺少一维信息，但仍能从地形草图上获取有价值的信息。草图是线条轮廓，它决定了地形起伏特征，多条轮廓线的遮挡关系可以确定不同轮廓的深浅关系，被遮挡的部分可以确定线条延伸也不会超出前层的可见部分。地形草图没有更多的信息可以挖掘，为了使地形可计算，初始状态先做以下设定：

(1)草图是正面视点的单点透视图，每条连续的轮廓线初始状态为一个平行于草图平面的深度层。由于这个平面是绘制的草图，不考虑图像畸变矫正。

(2)初始相对深度关系根据前后遮挡关系获得，被遮挡部分延伸时不能超过前层。

(3)每个深度层的轮廓线从最高点到两侧地面部分单调变化的称为一个地形单元，若单条连续轮廓线存在极小值，则拆分开处理。

(4)为了由二维扩展到三维进行计算，设定三维地形单元的垂直投影边界曲线初始状态为椭圆。

2.2 相对深度关系约束

小孔成像模型反映了真实世界三维空间到二维平面的映射关系，齐次坐标是摄影几何处理数据的有力工具，统一了常用图形变换和运算的处理方法，这种表示方法在深度成图方面有许多优点[32]。齐次坐标[x,y,ω]提供尺度不变性并满足仿射变换，其中ω=0对应于无限远投影平面，对于二维到三维的反向求逆问题，小孔成像模型如图2所示。

图2 小孔成像模型Fig.2 Pinhole camera model

小孔成像模型揭示了三维物体在二维平面上的投影规律。图2中S1和S2是真实三维空间的不同深度时的二维图像，其中f为焦距，z为目标距离，为了得到相对深度关系，不同深度层的二维图像采用齐次坐标表示，公式(1)由小孔成像原理导出。

(1)

可见当同一张二维图像在三维空间中的不同深度层时，其横纵轴数据都是成比例缩放的。而且根据第4条初始状态设定，垂直投影边界曲线初始状态为椭圆，当存在多个深度层的地形单元进行空间扩展后恢复到三维真实尺寸时，不同深度层三维扩展后在融合时不应存在更深层覆盖前层的三维空间，为了避免在三维椭圆扩展中出现这种情况，必须建立适当的约束条件，如公式(2)中的约束条件：

a1*ki-ai>bi*ki，(i=1...n),

(2)

其中：a1是为建模选定的基准层的深度值，ai是每个深度层的值，bi椭圆模型的短半轴，ki是比例系数。根据该递推约束公式，在给出基层深度a1和各层椭圆短半轴bi的基础上，可以从基准层依次递推出各层的临界深度值。在这个约束公式中，基准层深度的选择对于深度值的确定非常重要，将在第4.1节中进一步讨论。

3 关键算法

3.1 轮廓图像的预处理

在初始值及相对深度关系的约束下，需要将每个深度层变换到真实的投影面，并遵循摄影几何约束规则以不同的缩放系数放大不同深度层的草图轮廓线如图3所示，不同的缩放比例系数将提供不同的深度层缩放变化，选定最浅层为基准面，比例系数设定为对基准面的放大系数，不同的基准面深度的预设值会产生不同的三维建模效果。

图3 草图轮廓线深度分层Fig.3 Depth stratification of silhouettes sketch

图像在变换到相应深度层时，相应行的像素区域也将被放大。为了获得相应高度值，将图像进行填充、细化等处理，对于放大轮廓的像素值高度不单调变化的情况，每层图像与双向倾斜算子卷积以获得平滑图像数据后再提取高度值。

3.2 椭圆DEM扩展

DEM是地形数据经典的表示方式，高度值可以以DEM的形式存储，进行扩展补全后就能得到三维模型。根据2.1中的初始化设定，把整个地形拆分为多个两侧单调的地形单元计算，最后再把所有地形单元融合在一起形成整体三维模型。对于遮挡的轮廓线，以单侧曲线拟合的方式补全，且需要满足2.1中第二条约束，使补全的数据不能延伸超出前层范围。

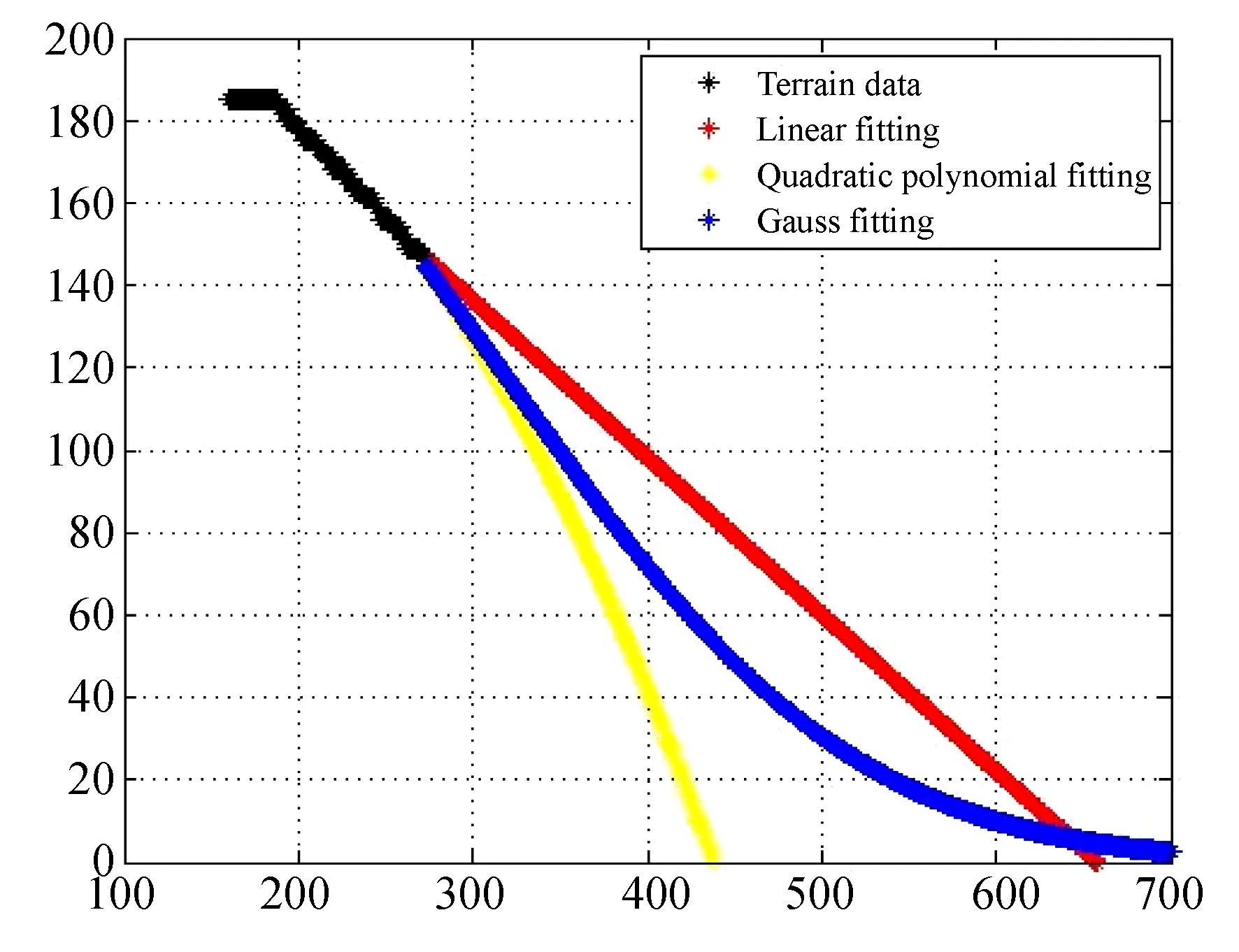
图4 数据拟合补全Fig.4 Data fitting and comparison

由于无法获取遮挡部分的任何信息，平缓和悬垂变化都是可能的。为了完成轮廓，本文使用了几个可计算函数来拟合现有的数据。利用多项式拟合，从脊线的最高点到两侧得到轮廓数据。然后使用曲线拟合来完成数据。如图4所示(彩图见期刊电子版)，黑线是非遮蔽数据，然后利用不同的拟合函数将数据拟合并完成到地面。红色为一阶多项式拟合的预测结果，蓝色为高斯拟合的预测结果，黄色为二阶多项式拟合的预测结果。二阶多项式拟合在末尾处下降较快，而高斯拟合在结尾处下降缓慢。定义前后遮挡轮廓线交点为遮挡点，拟合线与地面的交点为最终点，补全会存在超出或不超出前层遮挡的情况，当满足约束条件时，可以选择几种拟合方法之一补全数据。当几种拟合方式补全都超出约束时，补全数据没有合理的依据,直接利用遮挡点与完成点与之间的线性连接来保证补全数据的计算。

对于每个补全遮挡后的地形单元，建立椭圆模型进行扩展，以最高点为椭圆一侧焦点，两侧进行等高点的采样，最高点若离左侧近则为左焦点，离右侧近则选择为右焦点，参考采样点也从相同侧开始采样并寻找对应等高点，陡峭一侧开始采样能够保证选取等高对应点时不会由于采样点间隔近而出现一对多的情况。焦点与长轴的左右点确定后据椭圆方程计算出等高线图。如图5(a)所示，椭圆扩展计算后得到地形单元的DEM骨架图，右侧等高线间距明显是由于地形单元右侧地势平缓造成的。

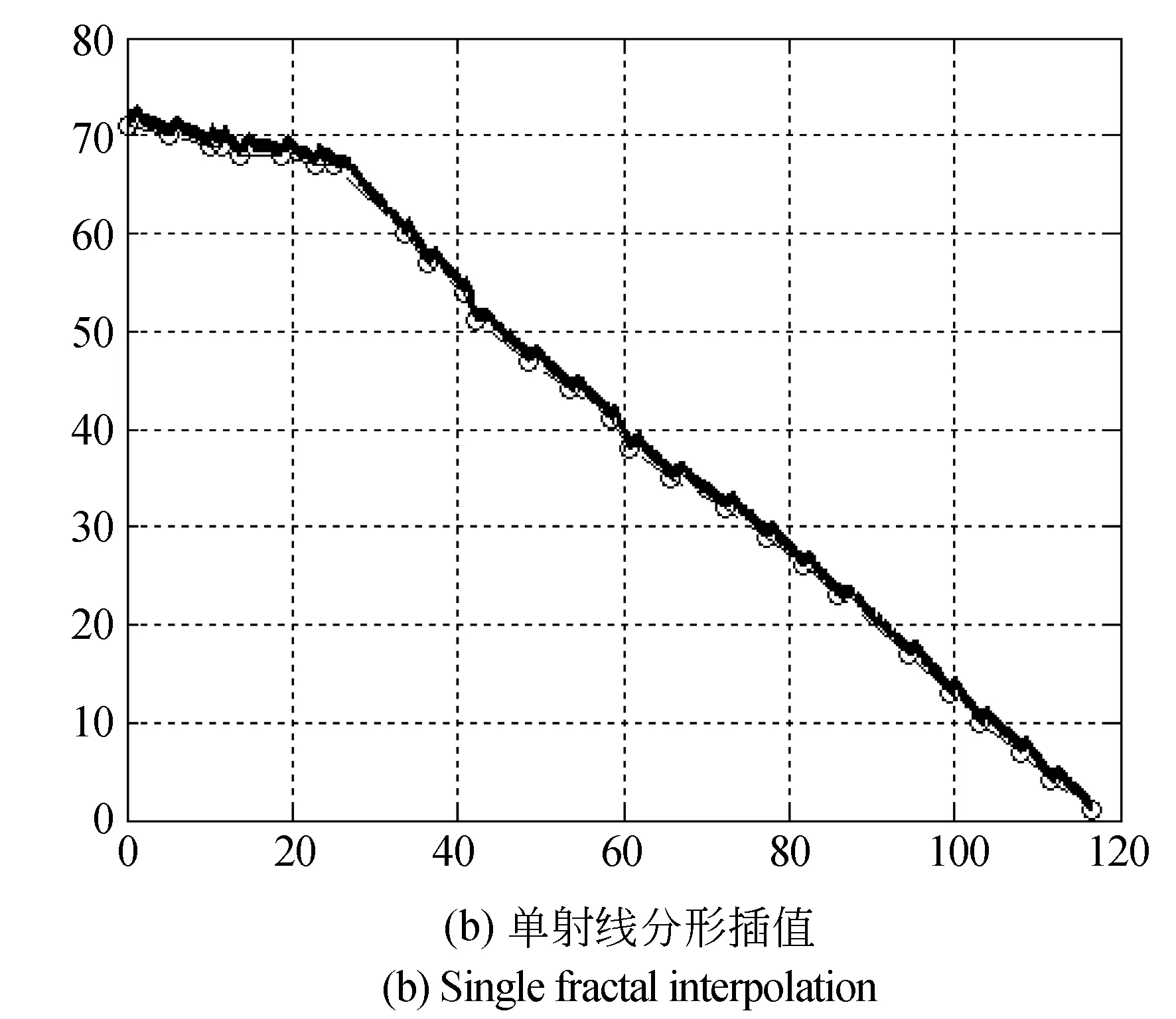
图5 周向分形插值Fig.5 Circumferential Fractal Interpolation

3.3 周向分形插值

等高线的计算得到地形要素的离散单元骨架，而等高线之间高程值的填充方法决定地形的真实实现，这是一个插值问题。由于地形有自相似的特点，根据相似性的内在规律，平滑插值不利于反映地形特征，因此本文采用分形插值方法[33]。等高线数据中，以焦点为起点沿梯度方向采集数据，计算单射线与等高线相交的数据点集，然后旋转角度继续采集。当从旋转角度采集数据时，它是由不同角度的射线与椭圆等高线相交得到的。当射线方向接近y轴时，线性方程的斜率过大，x采样次数过小。在x轴附近采样时，线性方程的斜率太小，y采样次数也太少。因此，为了最大限度采集数据，使用方程(3)来确保每条射线获得足够数量的集合。

(3)

其中：xi，yi为采集横纵坐标，θ为角度间隔，n为射线数,如图5(a)所示(彩图见期刊电子版)，采样的红色区域和白色区域分界线为±π/4时获取最多的采样集合，根据椭圆形状区域大小调整角度间隔，形状越大、采样间隔角度越小时得到更密集的骨架数据。

利用角度变化进行周向分形插值计算到密集的DEM骨架图后，单射线分形插值按式(4)进行：

(4)

其中：x0是起始点，xN是结束点，xni,yni是插值数值，an,en,cn,fn是插值系数，dn是纵向压缩比。图5(b)是单条射线采集点的分形插值结果，图5(c)旋转角度后多条采集点的分形插值的结果，压缩比取0.1，迭代2次，压缩比取值过大会造成插值数据变化过大的情况，插值后数据量很大，计算微分筛选变化率大的数值进行匹配选择。最后，采用双三次插值法对DEM密集骨架数据进行插值。

3.4 旋转映射

通过上述方法得到的地形单元是与草图平面平行的三维模型，而仅从草图线无法判断实际脊线的走向。为了能够计算得到多种不同情况的真实空间的，需要一个类似旋转的操作，但它与普通的旋转计算有本质的不同,在旋转过程中，由于需要保持在草图平面的一致性且符合摄影几何的规律，是非刚性的形变操作，所以以映射规则来进行形变达到目的。如图6(a)所示，O为视点，AB线为平行视图平面的方向，从O的角度来看，ARB和PRQ，MRN，PRN，MRQ，PRR2Q等都是与三维模型脊线投影相同的草图轮廓线。定义R为旋转点，R2为拐点，在真实三维空间中若形如R2的拐点加多，则会有更多空间位置的组合，即会存在无数种可能的组合，要得到它们都需要从初始的ARB变形获得。对于不存在诸如拐点R2的旋转情况，可直接通过旋转映射计算得到，AFB需要如图6(b)所示的映射，旋转成图后会发生变形，得到不同情况下的三维山体模型。对于存在拐点的情况需要分段旋转映射，从而完成三维空间模型的复原。

图6 旋转映射Fig.6 Rotation Mapping

旋转映射的复原步骤如下：

Step 1 在平行于草图平面的地形单元长轴AB上从左至右选取旋转点R，拐点Ri，i=2,3..N。N为选取的拐点个数。

Step 2 确定旋转方向，旋转方向可以是顺时针方向或逆时针方向。并设定旋转角度在转向较深的一侧为正，较浅一侧为负。

Step 3 地形单元的DEM数据根据旋转点进行旋转映射计算按照公式(5)计算：

(5)

式中：k为深度变化的比例系数，φ是旋转角度，x和y是原始位置，x′和y′是映射后位置，dis为距旋转点的距离。

Step 4 拐点Ri为新的旋转点，对新旋转点的右侧数据重复Step3的旋转映射公式进行计算。

Step 5 对映射造成的DEM数据空洞的部分采用双三次插值补全。

3.5 柏林噪声

草图并不具备具体的细节数据，柏林噪音能够很好的模拟自然特效[34]，随机地形的生成常使用柏林噪声制作，把它与DEM数据叠加可以丰富地形细节。使用3D柏林噪声，分形叠加可以使用不同频率和振幅进行叠加计算从而得到更加真实的地形效果[35]。

运用[36]中的方法进行噪声的计算，通过调整noise3(x/quality,y/quality,z)中z值及quality在多次叠加中的倍频值及迭代次数，得到不同的噪声数据，我们此处只是添加柏林噪声丰富细节，叠加到原DEM数据时进行小系数的加权运算以达到丰富地形细节的效果，在叠加后仍存在地形起伏剧烈的情况用高斯滤波进行平滑。

4 实验验证

符合轮廓线草图投影的三维地形模型存在无数种，按照本文方法可以恢复各种情况的真实三维空间模型，算法用Matlab实现，三维模型用WebGL进行渲染。实验中以图3中的草图为例，从相对深度关系基准层深度选取对空间位置影响，符合一致投影的三维空间恢复的旋转映射算法实验，及多层单元山体融合生成最终三维模型结果对比三方面验证第一人称视角地形轮廓草图的真实空间重建方法的有效性。

4.1 基准层深度取值影响

二维草图各深度层间只有相对深度关系的约束(公式(1))和各层间间隔的约束(公式(2))，基准深度层和各层间距离的设定影响到三维模型的空间位置。3.2描述的DEM拓展用的是椭圆模型，层间隔大于各地形单元的短半轴基本都能满足条件，为分析基准深度层取值的影响，层间间隔递推计算取刚好满足约束的深度值，图3中的草图选取离视点最近的层为基准层，各层在椭圆拓展计算的短半轴分别为39，75，117，96，设定基准深度为200，500，1 000，2 000进行4组相对深度递推计算。

从表1的4组相对深度值计算可见，基准层的深度值设定越大，比例值的增长率越低，深度层间的间隔越紧凑，当基准深度200变化到500时，可以看到深度层间隔在3到5层的间隔值变化很大，而在基准深度1 000变化到2 000时，只有4到5层的深度值有较小变化。说明基准深度层设定在大于1 000后，若按约束临界值取值时，间隔变化趋于平缓，各地形单元之间也更为紧凑。虽然大的间隔同样可以保证三维地形的生成，但更紧凑的空间布局更符合用户手绘草图的期望。

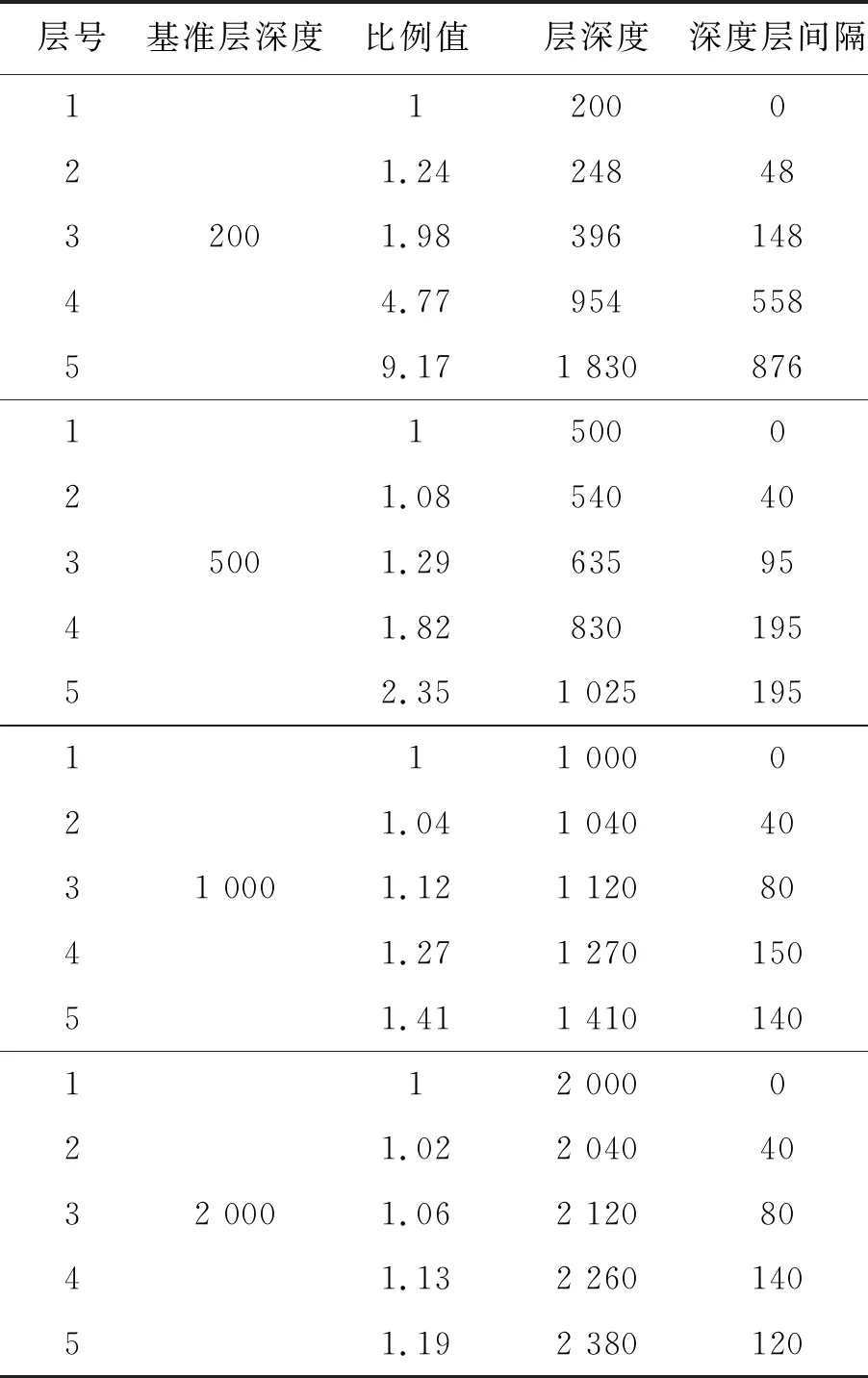
表1 相对深度计算

4.2 地形单元的旋转映射

本文提出的旋转映射算法实验中以单独地形单元进行5种典型情况的旋转映射进行分析，如图5所示，这6幅地形单元的俯视图具有同一视角下轮廓的真实空间形状。

在图5(a)中的俯视图是经过椭圆DEM扩展，周向分形插值后得到的平行于草图平面的初始地形单元，图5(b)是以左焦点为旋转点正方向45°旋转获得的，图5(c)是以左焦点为旋转点的反方向45°旋转获得的，图5(d)是左焦点为旋转点，左正右负旋转45°得到的，图5(e)是左焦点为旋转点，左负右正旋转45°映射得到的，图5(e)存在2个旋转点的情况，从左到右以负-正负的方向旋转得到的。可以看到，从初始状态旋转映射到不同空间形状后，俯视角度看，已经由椭圆变形为不同形状，是满足摄影几何的非刚性形变，实现了不同情况的三维模型在二维草图轮廓线一致的需求，完成了二维到三维的逆过程。

图7 地形单元旋转映射Fig.7 Terrain unit rotation mapping unit

4.3 地形单元融合

把各地形单元对齐并进行融合，得到由二维草图生成的最终三维地形模型。在融合过程中，把不同深度扩展后的地形单元放在同一空间中。空间区域的深度取为最深和最浅地形单元本身空间深度加上它们计算深度值之间的插值，宽度取最深层地形单元的宽度值。为了保证融合在同一空间不同深度层的地形单元在草图投影平面原样对齐，各地形单元的DEM拼接时，两侧增加的空间宽度值为各层根据公式(1)都放大到最深层后和原宽度的差求出来的。对于出现地形高程重合的部分，大的高程值覆盖小的值为最终高程，由于各地形单元的深度值都是在公式(2)的约束下计算的，保证了重合部分不会出现深层地形完全覆盖前层地形从而不符合草图原有遮挡的情况。

图6显示了其他3种第一人称视角下草图重建地形的结果及本文重建的结果，图6(a)的方法需要用户交互的绘制地形的轮廓线，山脊线和地面投影区域来生成地形；图6(b)仅仅需要绘制地形的轮廓线，通过轮廓线和真实世界的DEM数据进行匹配来获得地形数据从而实现地形构建；图6(c)的交互式方法更注重用户绘制的形状与走向控制；图6(d)是本文方法，直接从仅有的轮廓线自动计算生成地形；图6(e)是第二层与第五层地形单元进行旋转映射后进行融合的结果，在灯光渲染的效果下，可以从红色标记框的位置与图6(d)比较出不同，可见它们的真实空间位置是不同的，才会有不一样的阴影效果。图6(e)是加入了柏林噪声后的地形效果，可见随机效果是比较明显的，但仍能够保证地形轮廓基本与原草图一致，加权添加柏林噪声丰富地形细节的方案是可行的。图6(g)～6(i)是给出的几组重建示例，草图绘制山体形状嶙峋，重接结果也会体现其特征。与其他几种草图重建方法相比，本文仅仅需要绘制地形的轮廓线，并不需要额外的山脊线，投影区域等，而且现有的方法中都没有从研究真实空间位置的角度去重建地形。仅仅需要设定不同的关键参数就能自动计算得到地形的三维模型，更加符合二维草图逆复原三维地形空间的需求。

图8 草图重建地形结果Fig.8 3D terrain modeling results from sketch

5 结 论

本文针对第一人称视角下二维地形草图重建三维真实空间的问题，提出了完整的重建方法，介绍了仅有少量信息的草图重建三维地形的方法框架和基础假设。然后给出了图像处理步骤，椭圆DEM扩展完成草图图像数据到高程数据的变换。其次，提出的周向分形插值与旋转映射完成草图投影线一致，符合真实空间摄影几何约束的三维数据计算。最后，加权添加分形叠加的柏林噪声实现地形细节展示的效果。本文提出了一种单幅二维地形草图重建三维模型的新方法，建立了相对深度约束，解决了二维图像第一人称视角下的多层遮挡地形建模问题。实验结果表明：存在多个遮挡的地形草图，基准深度层设定若取值为约束临界值时，值给定越大，生成的三维地形越趋于紧凑，给定1 000可作为常规基准深度值的初值设置；旋转映射能够在给定旋转点后，实现任意符合同一投影草图轮廓的三维地形空间重建；多层遮挡的地形草图重建的三维模型能够实现原草图的多种真实空间位置布局，并能满足地形特征的展示。