临近空间风温遥感干涉仪设计及正演

何微微，武魁军，傅 頔，王后茂，李 娟

(1.武汉科技大学 城市学院，湖北 武汉 430083；2.中国科学院 武汉物理与数学研究所，湖北 武汉 430071；3.中国科学院 西安光学精密机械研究所，陕西 西安 710119；4.中国科学院 国家空间科学中心，北京 100190)

1 引 言

临近空间通常指高度介于20～100 km的大气层区域[1]。临近空间风温探测对于大气物理和空间科学的发展具有重要的学术意义。精确的风场与温度场探测对于研究中层大气的半年振荡[2]、大气潮汐结构的季节变化[3]、全球大气动量和能量的传播，以及球面大气中行星波的激发具有重要的科学意义[4-5]。 此外，大气风场温度场的精准探测，对于提高卫星发射的成功率、保障航空航天安全性、提高中长期天气预报的准确率具有十分重要的应用价值。

临近空间的探测设备非常丰富，但由于技术限制，大气风场、温度场的探测主要局限在地基遥感探测技术，如流星雷达[6]、拉曼测温激光雷达[7]、多普勒测风激光雷达[8]、气辉成像干涉仪[9]等。随着空间技术的不断发展，提出了具有全球观测尺度的星载风温探测手段。星载气辉成像干涉仪采用临边观测模式，具有垂直分辨率高、光谱分辨率高、相位灵敏度高的优势，已成为卫星遥感领域的前沿课题[10]。

星载成像干涉仪技术通常采用多普勒频移法获得风速，采用多普勒展宽法获得温度，即通过干涉图的相位变化获取气辉的多普勒频移信息以反演风速，通过干涉图对比度的变化获取气辉多普勒展宽信息以反演温度。由于干涉图的相位变化与对比度变化相比更敏感，风场反演精度高于温度场反演精度。然而，对处于热力学平衡态的双原子或多原子分子，可以采用双线比率法(即两条分离的辐射线的相对强度)确定大气温度。双线比率法可提高温度测量精度(约1～3 K)。1991年，搭载于上层大气研究卫星UARS的风场探测干涉仪-风成像干涉仪(WIND Imaging Interferometer，WINDII)与高分辨力多普勒成像仪(High Resolution Doppler Imager，HRDI)分别采用了多普勒展宽法、双线比率法两种测温方式。WINDII利用O原子的红线(630.0 nm)和绿线(557.7 nm)，测量了海拔75～320 km的风速(精度5～8 m/s)和温度(精度20～75 K)[11]。HRDI利用O2分子电子态跃迁 的(0,0)，(1,0)，(2,0)3个振动带的吸收及辐射光谱[12]，获得了平流层(10～40 km)到中间层与低热层(50～120 km)的大气风场(精度为5 m/s)和温度场(精度为7 K)[13]。

WINDII和HRDI取得成功之后，星载风温探测吸引了越来越多的关注，其发展趋势是将探测高度向较低海拔区域推进以获得更广泛的高度覆盖范围。加拿大 York大学研制的同温层风场输运干涉仪(Stratospheric Wind Interferometer for Transport studies，SWIFT) 采用Michelson干涉成像仪探测O3位于1 133.433 5 cm-1附近的振转光谱目标谱线[14]。2015年，Shepherd团队提出了SWIFT-DASH的改进方案，采用多普勒外差干涉仪(Doppler Asymmetric Spatial Heterodyne，DASH)替代Michelson干涉仪[15]。多普勒调制型分子滤光器(Doppler Wind and Temperature Sounder，DWTS)采用分子滤光技术，可同时获取多普勒频移和辐射线宽信息，从而实现25～250 km的连续风温探测[16-17]。由于目标谱线均采用了中波红外(Mid-wavelength Infared,MWIR)和长波红外(Long-wavelength Infared,LWIR)辐射线的设计策略，SWIFT和DWTS的优势具备全天时风温探测的能力。然而，工作在MWIR或LWIR波段的星载红外遥感器系统通常会受到来自光学元件热背景的强烈干扰，测量不确定性较大。鉴于此，红外遥感系统平台需要较低的制冷温度，因此增加了平台成本，但SWIFT的温度测量能力依旧相对较低。此外，DWTS的模拟结果表明，在50～100 km的高度内，DWTS无法获得垂直轨道方向的风速分量；100～250 km高度内，虽然可以获得垂直轨道方向分量的风速，但其不确定度是沿轨方向风速分量的10倍。

根据加拿大中层大气模型[18]，一项科学研究表明，为了改善天气预报系统中的数据同化分析精度，40～60 km高度内，风速精度需达到5～10 m/s，温度精度需达到5～10 K[19]。针对临近空间的探测需求，可利用O2分子的红外大气带(跃迁)1.27 μm波段的气辉为目标谱线。鉴于O2(a1Δg)气辉的辐射强度相对较强、自吸收能力相对较弱，适用于45～90 km高度内的风温探测。加拿大StaSci计划部署的中间层成像迈克尔逊干涉仪(Mesospheric Imaging Michelson Interferometer，MIMI)以及NASA的MIDEX计划支持的波成像迈克尔逊干涉仪(Waves Michelson Interferometer,WAMI)均采用该谱带的强、弱两组气辉谱线(每组3条)进行风温探测[20]。中国科学院武汉物理与数学研究所的武魁军等人利用O2分子1.27 μm近红外气辉对临近空间风温探测精度进行了研究[21-23]，并分析了氢氧气辉对1.27 μm气辉风温探测精度的影响[24]。

本文提出了临近空间风温探测干涉仪(Near-space Wind and Temperature Sensing Interferometer，NWTSI)仪器模型，通过广角迈克尔逊干涉仪观察1.27 μm波段的O2(a1Δg)气辉，实现临近空间风场、温度场的星载遥感探测。与WAMI和MIMI类似, NWTSI重点关注低海拔区域(40～80 km)。NWTSI采用迈克尔逊干涉仪，由多普勒频移法获得风速，由双线比率法获得温度，具有较高的风温探测精度。本文介绍了NWTSI仪器模型，分析了大气临边辐射光谱的特性并对NWTSI进行了正演仿真模拟，最后讨论了风温探测的不确定度。

2 仪器模型

NWTSI是一种基于广角迈克尔逊干涉仪的星载风温遥感探测载荷。它通过临边观测的方式，在两个相互正交的观测方向上交替观测。交替观测由指向镜将视场(Field of View,FOV)指向相应的观测方向实现，视场角为1.5°，高度覆盖20～120 km。NWTSI 前后两个视场可先后观测到相同的大气区域，在410 km的高度上观测间隔大约为9 min。

图1为NWTSI仪器模型的光学系统示意图。该仪器参考了WAMI的仪器设计，由两个望远镜、一个迈克尔逊干涉仪、一个窄带滤光片、一个法布里-珀罗(F-P)标准具以及一个近红外焦平面组成。视场由望远镜1(telescope 1)和视场光阑(FS1)决定。入射光由指向镜进入望远镜1，然后入射到迈克尔逊干涉仪。望远镜1的角放大率为2，则迈克尔逊干涉仪的视场为3°×3°。迈克尔逊干涉仪长壁(LPA)的反射镜分为厚度不同的四等份，每一分区较上一分区光程差(Optical Path Difference,OPD)增加λ/4，则四分区之间的阶跃光程差为λ/4，λ/2和3λ/4。四分区的设计可实现4个干涉图样的同时采集，与WINDII的顺序采集相比，该方法有效避免了测量过程中强度变化引起的误差。迈克尔逊干涉仪短壁(SPA)的反射镜安装在电容式位置传感器控制的压电器件上，则干涉仪镜子也可以步进，用于实现飞行期间的校准。平面镜M3的作用是将光学元件折叠成紧凑的形状。入射光经视场光阑FS2后进入望远镜2。望远镜2的角放大率为0.5，因此，滤光系统的视场再次变为1.5°×1.5°。迈克尔逊有视场展宽的能力，受视场角影响小，而F-P干涉仪透射函数却受视场角的影响很大，该设计的主要意图是有效解决F-P干涉仪视场角受限的问题。F-P标准具与干涉滤光片(F1与F2)共同作用实现目标辐射线的分离，同时阻止散射太阳光的进入。望远镜2聚焦在F-P标准具后面的金字塔棱镜上。棱镜的边缘与迈克尔逊干涉仪长壁反射镜的边缘部分对齐，使得入射光投影到焦平面阵列(Focal Plane Array,FPA)的不同区域，每个区域对应不同的阶跃相位。棱镜后设置有分束镜(BS)，将光路分为两个通道：强线通道与弱线通道。表1为NWTSI仪器的系统参数。

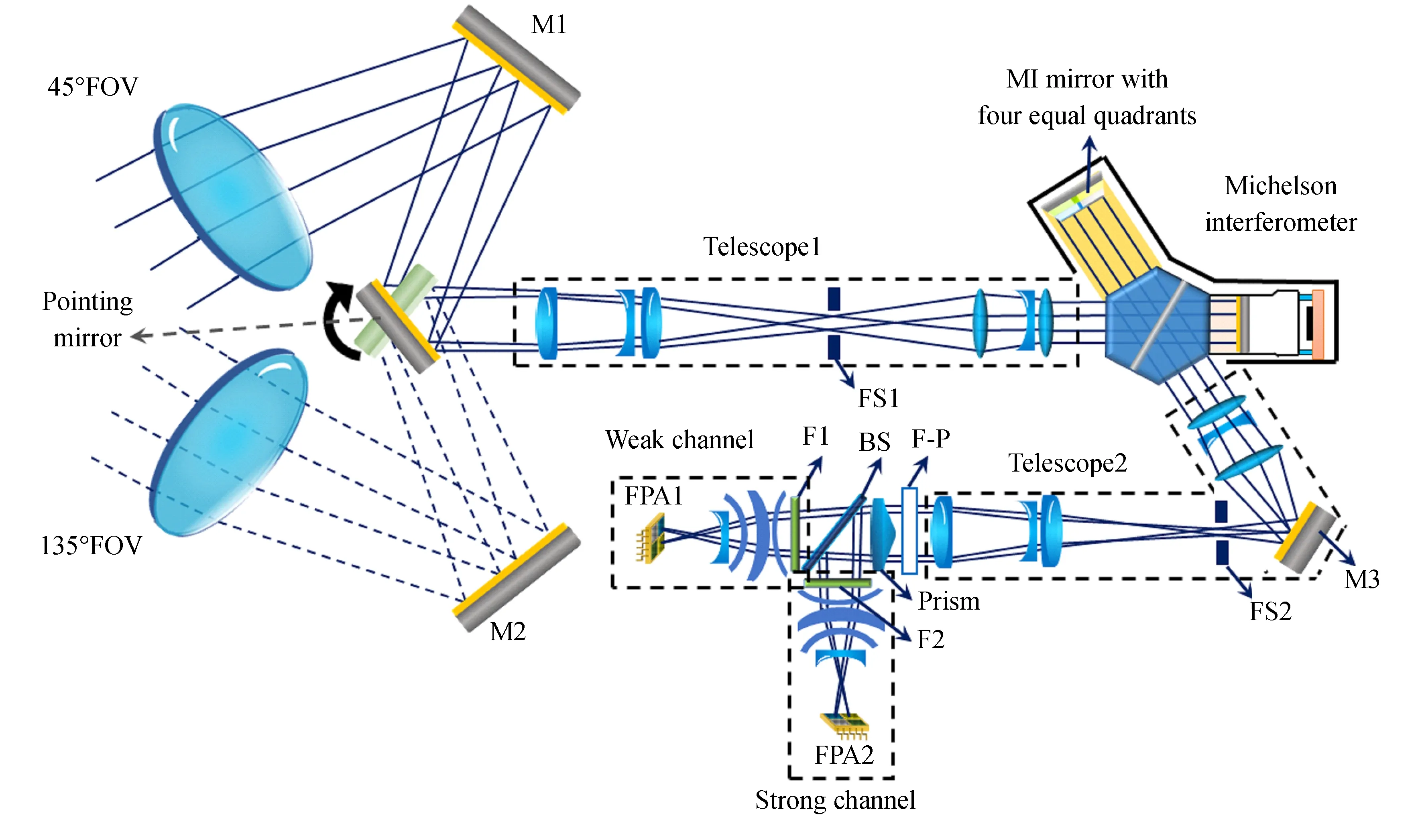
图1 临近空间风温探测干涉仪的光学原理图Fig.1 Optical schematic of near-space wind and temperature sensing interferometer (NWTSI)

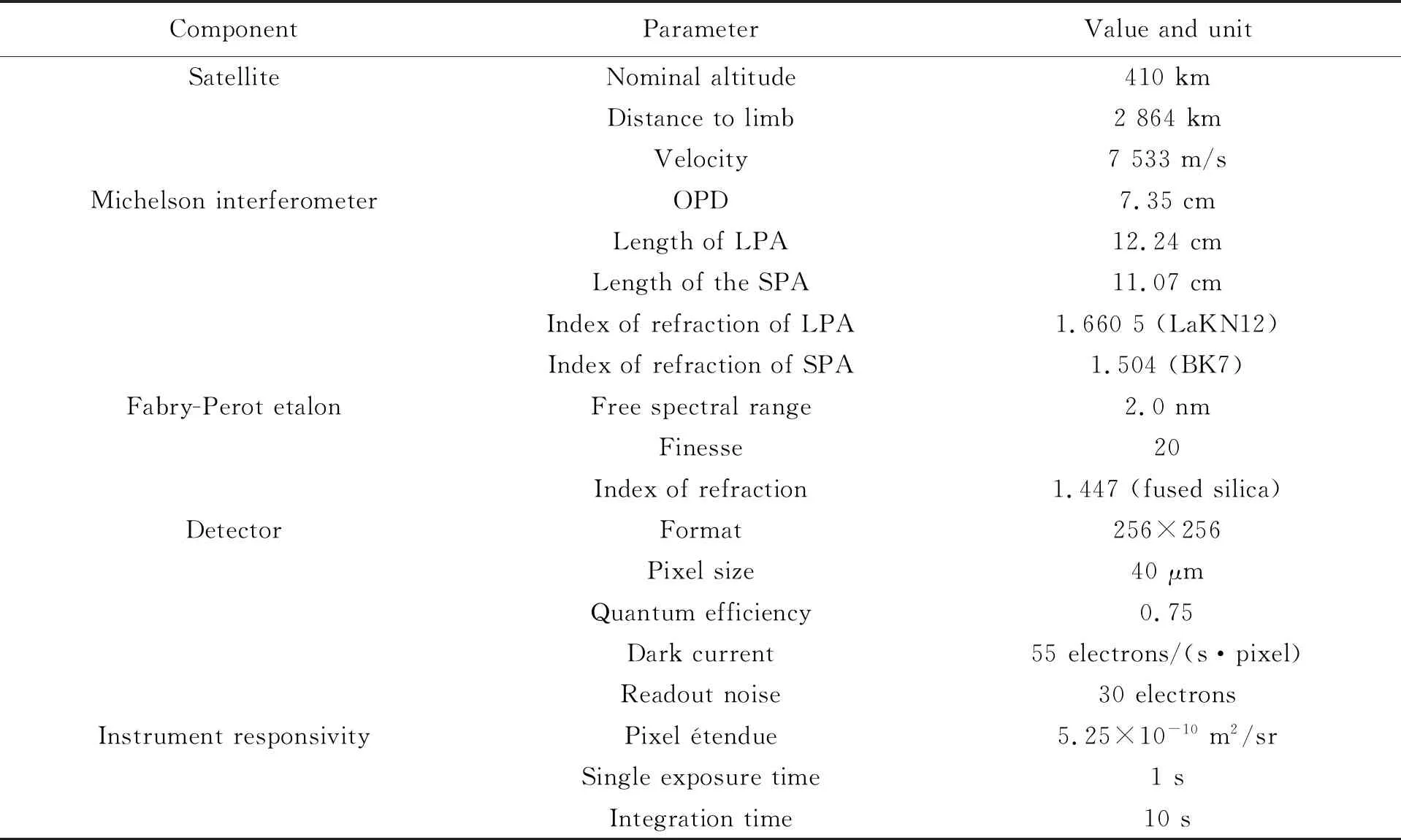
表1 临近空间风温探测干涉仪的系统参数

3 仿 真

正演仿真的目的是模拟仪器的功能和效果，产生预期的干涉图像。通过测量仿真可以实现仪器性能的独立分析，并可对仪器性能做出评估。正演模型包含大气辐射模块，迈克尔逊干涉仪模块，滤波器模块，以及光学系统、传感器阵列、红外焦平面等设备的系统参数。

3.1 正演仿真

3.1.1 大气辐射

1.27 μm气辉具有辐射强度强、高度覆盖范围广的优势，是全球大气风温遥感的最佳目标谱线之一[25]。1.27 μm气辉主要来源于O2第一激发态O2(a1Δg)到基态O2(X3Σg)的跃迁。实际电子跃迁过程中，振动态和转动态的存在，使得1.27 μm氧气辉成为包含约150条辐射线的光谱带。

O2(a1Δg)气辉临边辐射光谱由沿视向的路径积分计算获得。积分过程中大气被分成许多离散的薄层，每一层都被视为是均匀的，逐层计算的辐射传输方程表示为：

L(v)l=L(v)l-1exp(-∑α(v)l,iul)+

(1)

其中：J(ν)l,i与α(ν)l,i分别是第i条临边观测路径、第l层大气的辐射源函数与吸收系数；ul=nl(ZU-ZL)是第l层大气的O2分子的分子柱密度；ZU与ZL是第l层大气上、下边界的临边切点高度。

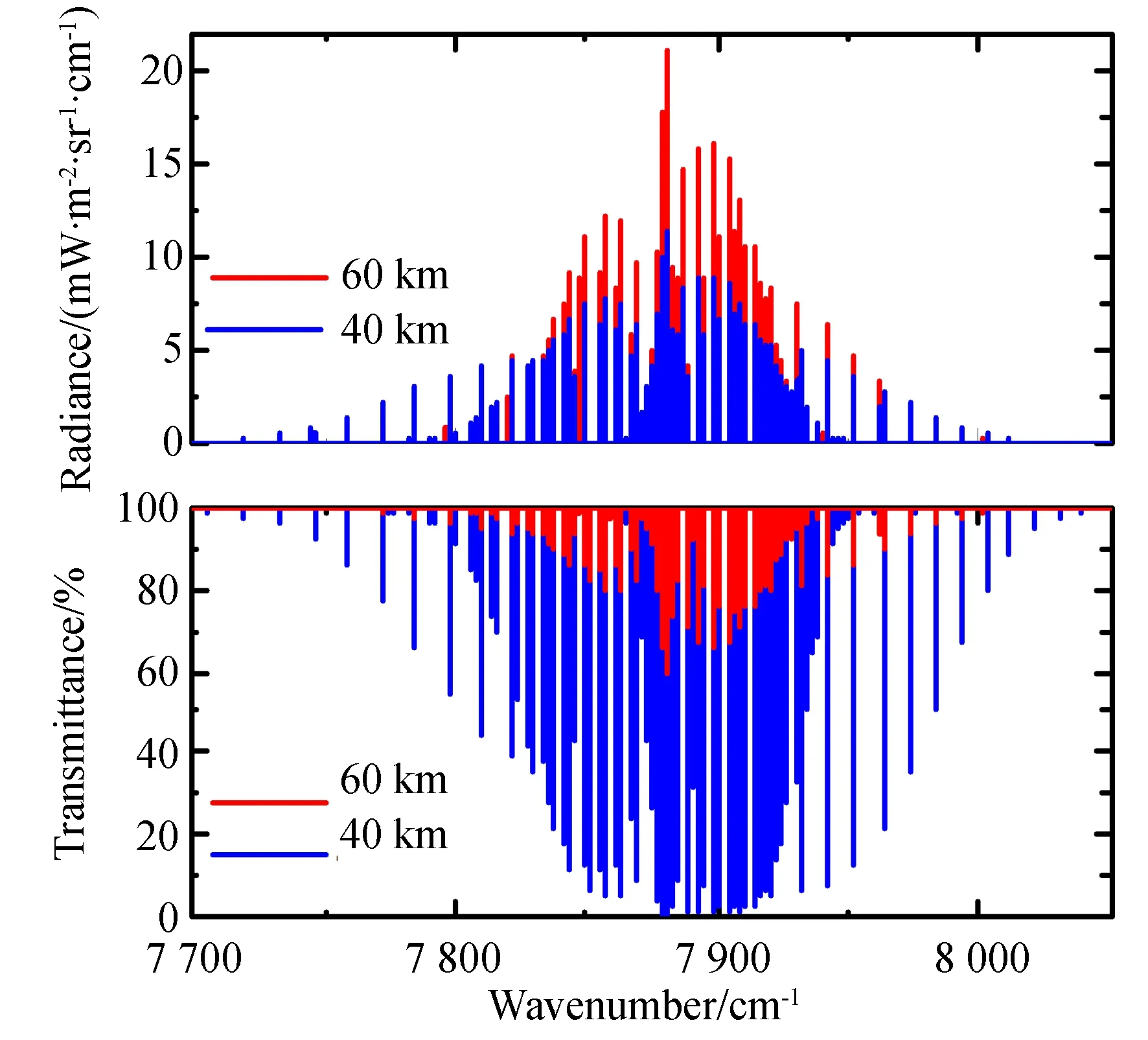
图2 O2红外大气波段在40，60 km切点高度上的辐射光谱与透射谱Fig.2 Limb radiance and transmittance spectra of O2 infrared atmospheric band at tangent heights of 40 km and 60 km

图2描述了临边切点高度为40 km和60 km，不考虑大气风场与卫星速度时O2(a1Δg)红外大气带的临边辐射和透射光谱。图中红线代表临边辐射光谱，蓝线代表临边透射光谱(彩图见期刊电子版)。可见，处于大气带中心位置的辐射光谱具有较强的辐射强度，但两翼位置处的辐射光谱自吸收效应较弱，并且辐射强度与吸收系数均随切点高度的变化而变化。因此，两翼位置处的辐射光谱适合低海拔区域的风温探测，而中间区域的辐射光谱适合高海拔区域。

在众多的辐射光谱中选择最佳的目标谱线是星载风温成像干涉仪研制的关键之一。Ward等人提出了系统的选线标准[21]，即目标谱线的选取需遵循三个原则：温度灵敏度高，谱线分离性好和高度覆盖范围广。NWTSI目标谱线的选取参考了WAMI与MIMI的选线方案，选用强线组与弱线组共6条谱线，每组包含3条谱线。强线组谱线波数分别为：7 908.973 6 cm-1，7 909.653 5 cm-1，7 911.013 3 cm-1；弱线组谱线为：7 821.110 5 cm-1，7 822.221 6 cm-1，7 822.952 5 cm-1。20～60 km的低空区域存在较强的自吸收现象，选用弱线来减少自吸收对反演的影响；60～120 km的高空区域体辐射率相对较低，信号也相对较弱，但高空的自吸收效应几乎不存在，可选用强线探测，增大信噪比，提高测风精度。强、弱线的联合使用能够覆盖20～120 km的临近空间区域，既避免了低空自吸收效应对风温探测带来的影响，又保证了高空风温探测的精度。

3.1.2 滤波器

O2分子的1.27 μm辐射带包含数量众多并且分布十分密集的谱线。为了实现目标谱线的分离，滤光系统需要有大约0.1 nm的带宽。因此，需将F-P标准具与窄带滤波器联合使用。此外，窄带滤波器还具备降低背景光亮度、提高条纹对比度的作用。

NWTSI的滤波系统由F-P标准具和窄带滤波器(F1和F2)组成。系统的总滤波函数由二者共同决定。F-P标准具的带通滤波函数采用Airy 函数模型，如式(2)所示，设计参数如表1所示。

(2)

其中：σ是入射光的波数，r是标准具的反射率，netal是标准具材料的折射率，d是标准具材料的厚度，θ是标准具腔内的折射角。

图3 弱线组与强线组的最佳透射函数Fig.3 Optimal transmittance functions of weak group and strong group

采用双线比率法获得温度信息，NWTSI要在同一视场中同时观察3条谱线。为了降低成本，只使用一个标准具，其后利用分束镜将光线分离为弱线、强线两个通道。图3给出了强线组与弱线组的最佳透射率函数。图中S1: 7 908.97 cm-1,S2: 7 909.65 cm-1,S3: 7 911.01 cm-1；W1: 7 821.11 cm-1,W2: 7 822.22 cm-1,W3: 7 822.95 cm-1。

3.1.3 迈克尔逊干涉仪

迈克尔逊干涉仪的光程差随离轴角的变化如下[25]：

(3)

其中：nL与nS分别是迈克尔逊干涉仪长臂和短臂的折射率；i是像素离轴角；tL与tS分别是干涉仪长臂和短臂的长度。迈克尔逊干涉仪的光学参数如表1所示。将式(3)应用于每个像素，可得光程差的像素分布如图4所示。

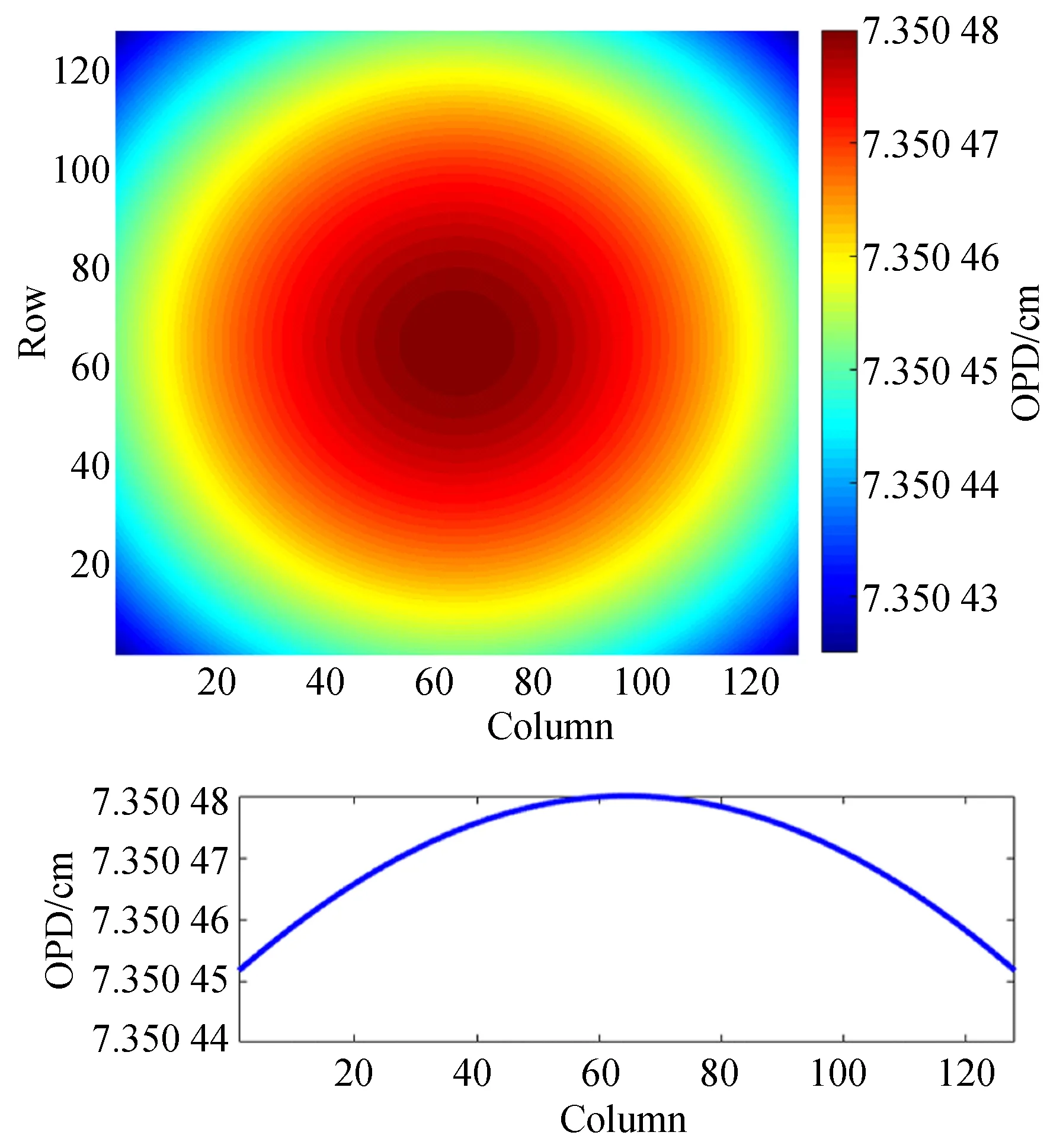
图4 迈克尔逊干涉仪的光程差像素分布Fig.4 Pixel distribution of optical path difference of Michelson interferometer

步进相位(k-1)/2π，(k=1,2,3,4)，通常指的是视场几何中心位置处的步进相位。每个像素第k次步进的相位可表示为：

(4)

其中d是迈克尔逊干涉仪的步进尺寸。

利用迈克尔逊干涉仪的相位，以及滤波器的带通滤波函数，结合图2中的临边光谱辐射特性，即可获得NWTSI的干涉图像。

3.2 测量仿真

图像的像素值由大气辐射传输方程(式(1))干涉图决定。给定像素的干涉图可表示为[25]：

[1+Uljcos(2πvΔlj+φklj]dv,

(5)

其中：Iklj为第l行第j列第k次步进的干涉图，flj(v)是相对总滤波函数，Ulj是仪器可见度，Δlj是光程差，φklj是迈克尔逊干涉仪第k次的步进相位，ν是波数，Rlj是仪器响应度。Rlj可定义为[22]：

(6)

其中：AΩ是光学系统的光学扩展量，t是干涉时间，q是探测器的量子效率，h是普朗克常量，c是真空光速，τ是滤波器与光学系统的透过率，v0是O2辐射线的中心波长。

大气风场的精准测量需要较大的视场，从而获得较大的响应度。增加入射光立体角Ω的尺寸可以增大响应度，但这会使得光程差增加，引起条纹对比度的降低。因此，传统仪器在立体角的扩大上有一定的局限性。NWTSI仪器临边观测视场为1.5°×1.5°，第一台望远镜的角放大率为2，则迈克尔逊干涉仪的视场为3°×3°。根据视场展宽原理，迈克尔逊干涉仪可以保证在大光学扩展量的情况下实现高分辨率。然而，F-P标准具的立体角则受限于：

ΩFP=2πn2/RFP,

(7)

其中RFP=σ0/δσFP，为F-P标准具的分辨率。因此，望远镜2的角度放大率设计为0.5，则F-P标准具的视场再次变为1.5°×1.5°。

WINDII的测量方式采用逐像素测量的四点采样法，即通过比较四步进所得的干涉图像获得多普勒风引起的干涉图相移，最终反演得到风速。NWTSI的四分区设计则可以实现4个干涉图样的同时采集，并通过金字塔形棱镜同时成像在FPA的4个不同区域。通过比较FPA不同区域干涉图的相移即可实现大气风场的探测。

图5所示为强线组与弱线组4个阶跃相位的干涉图像的正演仿真。如图5所示，干涉图样与像素位置、阶跃相位、滤波透过函数在视场上的变化、以及临边辐射光谱随切点高度的变化均有相关性。干涉图样中的每个像素代表对应空间区域临边辐射光谱的积分强度。NWTSI对应的空间区域尺寸约为1 km × 1 km。像素间干涉图样的差异主要来自于临边观测气辉强度随切点高度的变化，以及光学系统对干涉图样的调制。正演仿真过程中，气辉光谱辐射只考虑垂直方向的变化，忽略视场相对于地平线的倾斜以及地球的曲率，并假设仪器可见度和响应度对所有像素均相同。

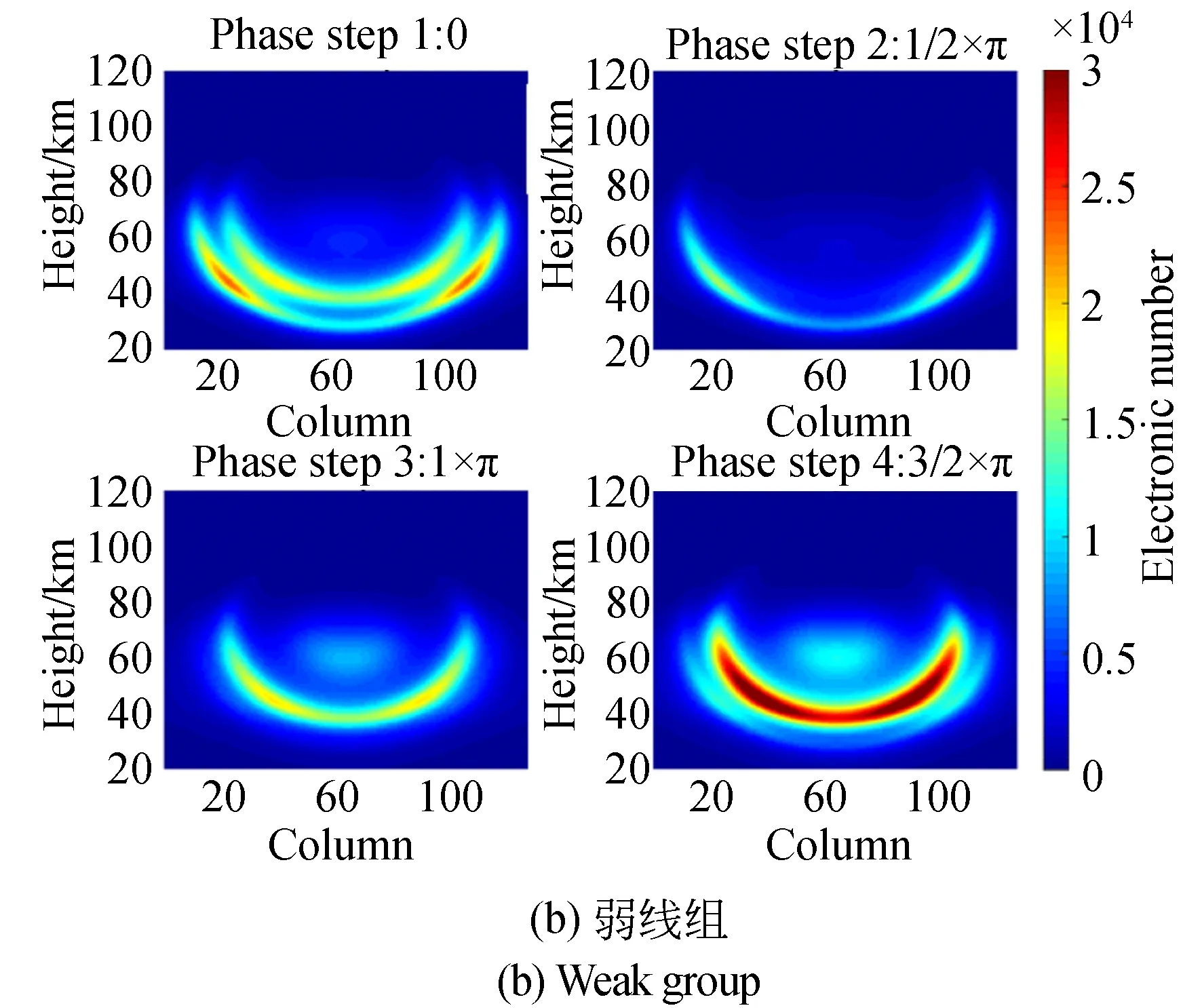
图5 四个阶跃相位的正演仿真干涉图像Fig.5 Forward simulation of interference images for four phase steps

探测器第l行第j列像素的干涉图总相位可以通过四点采样法得到。总相位减去地球自转相位、卫星运动相位以及仪器相位即可得到风场引起的相位。与地基观测技术相比，临边观测仪器的光学扩展量要小的多，然而，由于临边观测具有较长的积分路径，使得临边辐射谱的强度远大于地基观测的强度。

大气风场、温度场测量的精度受到信噪比(Signal-to-Noise Ratio,SNR)和临边观测权重的共同影响。在干涉图像的模拟中考虑了3种主要的噪声源，即散粒噪声、读出噪声以及探测器暗噪声(相关数据如表1所示)。强线组与弱线组的SNR和临边观测权重随高度的变化如图6所示。由图可见，强线组的SNR峰值位于40～45 km处，在该区域外缓慢下降，且在小于40 km区域下降得更快。强线组的SNR在较高的海拔区域(约60 km)达到峰值。低海拔区域O2(a1Δg)态的碰撞淬灭作用，导致态密度衰减，从而使得临边观测权重随切点高度的减小而减小。

图6 信噪比与临边观测权重随高度的变化Fig.6 Signal-to-noise ratio (SNR) and limb-view weight as functions of altitude

4 误差分析

依据光程差的变化，像素干涉图可以表示为截断傅里叶级数。傅里叶系数J1，J2和J3(也称为表观量)与干涉图相关[26]。风和温度的测量不确定度可以通过误差传递来确定。风和温度可以由表观量J1，J2和J3导出。视向风可由J2和J3计算得到，大气温度由J1确定。

(8)

4.1 风速误差

风速vw可以由干涉图的相移δφ获得[25]：

(9)

其中:c代表真空光速，相位φ可以式(10)计算[22]：

(10)

每一个像素都可以计算得到视向风以及随机误差。视向风的随机方差为[26]：

(11)

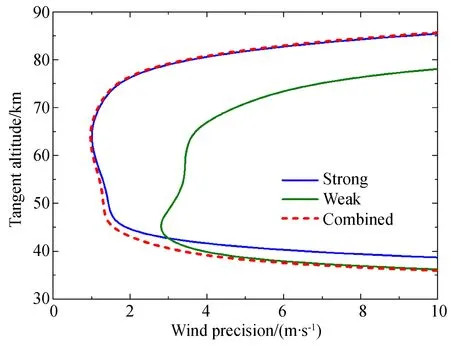
图7 强线组(蓝线)、弱线组(绿线)辐射线以及联合谱线(红线)多普勒风测量的随机误差标准差Fig.7 Random error standard deviation of Doppler wind by strong(blue line) and weak groups(green line) and combined lines (red line)

图7所示为强线组与弱线组两组辐射线风速测量的随机误差标准差(彩图见期刊电子版)。由图可见，对于低海拔区域(低于42 km)的风速探测，使用弱辐射线更加精确，而高海拔区域使用强线更有优势。这是由于强辐射线在低空具有强烈的自吸收效应(如图1所示)。

4.2 温度误差

大气温度由温度敏感性不同的两条独立辐射线的吸收率的比值决定[27]，即有：

(12)

式中：E″是跃迁的低态能级的能量；S0(T)为参考温度T0=296 K时的线强度，A是辐射线的吸收率积分，h与kB分别是普朗克常量与玻尔兹曼常量。

温度的不确定度由线强度和吸收率积分的不确定度决定，可表示为[28]：

(13)

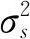
吸收率积分的不确定度主要来自干涉图平均值J1的信噪比。线强度不确定度是由固有不确定度ΔS(T0)与温度相关的不确定度ΔST(T)的传递引起的。ΔS(T0)可以由数据库获得[28]，ΔST(T)与线强度成正比：

(14)

式中Q(T)是分子配分函数。

图8所示为强线组与弱线组温度探测的随机误差标准偏差分布(彩图见期刊电子版)。由图可见，弱线组在切点高度40～75 km区域的随机误差水平为1.5～2 K，强线组的误差约为2～3 K。高海拔区域由于信号较弱，误差水平较大。测温精度除了受信噪比影响以外，还与跃迁的低态能级的能量差有关，弱线组测温精度高于强线组的原因在于它的低态能级的能量差比强线组大。

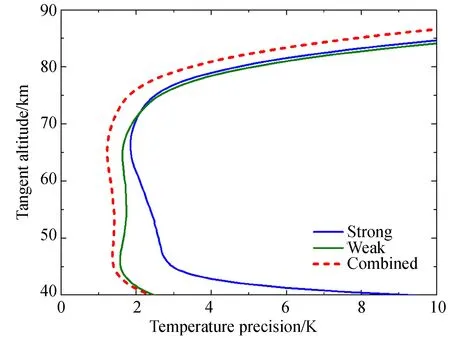
图8 强线组(蓝线)与弱线组以及联合谱线(绿线)以及联合谱线(红线)温度探测的随机误差标准偏差分布Fig.8 Temperature error profiles by using three emission lines in strong(blue line) and weak groups(green line)and combined lines (red line)

5 结 论

本文设计了临近空间风温遥感干涉仪，以1.27 μm附近的O2(a1Δg)气辉为目标源，采用广角迈克尔逊干涉仪，实现了临近空间区域风场、温度场的同时探测。首先通过逐行积分算法，并结合最新光化学反应模型(包含光谱参数、速率常数和太阳通量)，开发了O2(a1Δg)气辉临边辐射光谱的辐射传输模型。与WINDII和HRDI等其他风温干涉仪不同，NWTSI利用两组强度不同的目标谱线，仅对临近空间区域进行风温探测。按照谱线选取的原则选择了7 820～7 824 cm-1内的3条谱线组成弱线组，7 908～7 912 cm-1内的3条谱线组成强线组。弱线用于低空探测，以避免自吸收效应对测量结果的影响；强线用于高空探测，以实现高的测量精度。此外，建立了由大气辐射传输模块，迈克尔逊干涉仪模块，滤波器模块，以及光学系统、传感器阵列、红外焦平面等设备的系统参数组成的正演模型，并计算得到了强线组与弱线组的正演仿真干涉图。通过正演模型获得了临边观测图像，并对风速及温度的测量不确定度进行了计算分析。风温探测的精度受到了信噪比和临边观测权重的共同作用。由于低海拔区域O2(a1Δg)态的碰撞淬灭效应，临边观测权重随高度的降低而降低，导致低海拔区域探测精确度的降低。模拟结果表明，风速测量精度为1～3 m/s，温度测量精度为1～3 K，水平分辨率沿视线约350 km，在40～80 km高度内沿轨道约170 km，满足临近空间风温探测精度的要求。