对抗样本训练图分类器进行模型推理质量评估

于千城 ，於志文 ，王 柱

1.西北工业大学 计算机学院，西安 710072

2.陕西省嵌入式系统技术重点实验室（西北工业大学），西安 710072

1 引言

从社区结构这一中观层面对社交网络进行研究对人们准确理解社交网络的特性有十分重要的意义，既能够弥补宏观层面粒度过粗所造成的很多网络特性无法观察到的缺陷，又避免了微观层面粒度过细所带来的丢失共性并且计算复杂度高等问题。为了避免社区发现算法中手工预先设置社区个数，采用非参数贝叶斯层次模型来生成带重叠社区结构的网络，假设在无限可交换观测序列中可能存在无限多个社区，从而允许社区个数和模型参数的个数会随着观测数据的增多而增加。

本文主要关注计数值社交网络中的重叠社区分析问题，通过将无限潜特征模型[1]推广应用到关系型数据，提出了一个非参数贝叶斯层次模型[2]作为网络生成模型的重叠社区检测方法，采用负二项过程对似然分布进行描述，采用印度自助餐馆过程（Indian Buffet Process，IBP[3）]作为社区隶属指派矩阵Z的先验。采用马尔可夫链蒙特卡罗方法（Markov Chain Monte Carlo，MCMC[4）]对模型进行后验推理。

对关系型无限潜特征模型（rILFM）进行MCMC 后验推理后，得到的社区隶属指派矩阵Z的后验结果是一个N×K列的0、1 矩阵上的概率分布。对于单变量模型参数，很容易进行后验推理结果总结和推理质量评估[5-6]。然而，如何对这种带结构的多变量参数的后验推理结果进行总结和推理质量评估，目前尚未有比较好的方法。本文提出了一种基于对抗样本训练图分类器来进行推理结果总结和推理质量估计。通过将对抗样本和正常样本一起训练，提高了图分类器的稳定性。

2 网络生成模型

令G=(V,E) 表示一个有向图，Gt=(Vt,Et) 表示t时刻某一特定时间段对应的网络快照。结点集合Vt={v1,v2,…,vn}，结点个数|Vt|=n，边集合Et，每一条边eij关联一个计数值mij表示该时间段内由结点vi发起的与结点vj的交互次数。对于每个网络快照对应的计数值邻接矩阵M，定义在其上的是一个负二项分布mij～NB(rij,p)。对M进行泊松因子分解[7]，可以得到M=ZΛZT。综上所述，网络生成模型的生成过程如下：

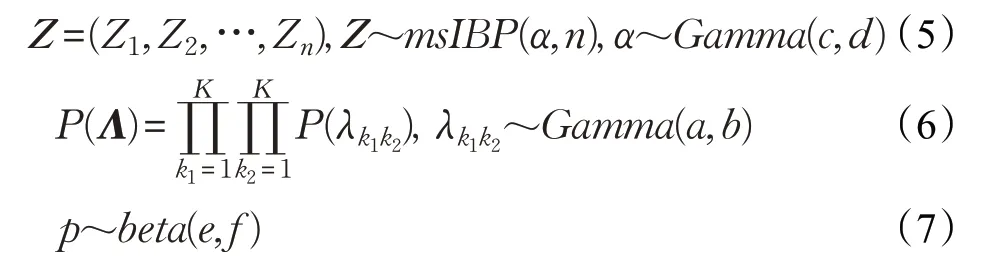
由可交换性假设可知，网络中的每条边都是条件独立同分布的，因此得到式（1）；式（2）～（4）由负二项因子分解[7]得到，式（3）表示对于结点i和j的每一个可能的社区隶属对＜zik1=1，zjk2=1 ＞所导致的结点间交互次数计数值为；式（5）表示Z的先验是一个IBP，其参数是n和α；式（6）表示社区兼容矩阵Λ中的K×K个值独立同分布于伽马分布；网络生成模型所对应的概率图模型如图1所示。

图1 网络生成模型所对应的概率图模型

直接采用了SBM（Stochastic Block Model，随机块模型[8]）的基本原理，即结点间连边的概率由结点所隶属的社区所决定，并且假定社区隶属是促进结点连边的。

3 通过截棍过程构造IBP

IBP作为先验时，对应的CRMW通常只有不含原子的非负随机质量全体Wf，只有当给出观测数据后才会将含固定原子的非负随机质量全体Wr引入到后验中。对于Wf，因为W͂是齐次NRMI，所以随机位置独立同分布采样自μ0，随机质量与[S,∞)上的具有指数倾斜强度测度ρ′(ds)=e-Usρ(ds)的泊松随机测度同分布，可以采用Ogata等提出的adaptive thinning方法进行采样[9]。

Thinning是Lewis和Shedler[10]提出的从一个泊松随机测度进行采样的方法，分为两步：首先从一个提议分布（一个比目标分布强度更高的泊松随机测度）采样出一些点，然后以提议分布和目标分布的强度之比作为概率接受或拒绝每个采样。如图2所示，在Adaptive thinning 算法中，从提议分布中采样点时，从截断级别S出发从左向右迭代进行，令ν′(s)是ρ′(ds)在 Lebesgue 测度下的密度，对于任意的t∈ℝ+，存在一个函数wt(s)满足wt(t)=ν′(t)和wt(s)≥wt′(s)≥ν′(s)（对于任意的s,t′≥t）。

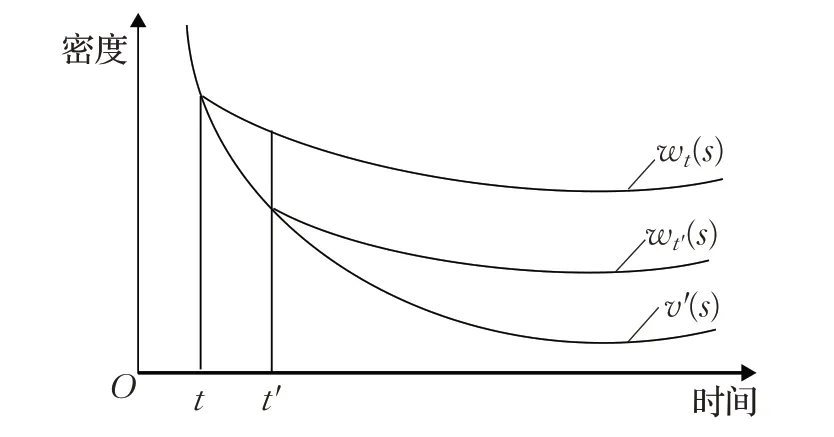
图2 从一个泊松随机测度进行采样时采用的渐进界限

算法1通过截棍过程构造IBP

3.返回N（N就是对强度为ν′的IBP 在[S,∞)进行的有限采样）

4 模型后验推理

由于社区隶属指派矩阵Z的每个元素zik指明了结点i是否隶属于社区k，因此网络重叠社区检测结果就可以从矩阵Z的后验分布中采样得到。由贝叶斯公式可知P(zik|⋅)∝P(M|Z,r,p)P(zik|Z-ik) ，其中Z-ik表示Z中除zik之外的其他元素。

IBP是严格稳定分布天然的指数族分布，采用指数倾斜可以在求解贝叶斯估计的近似公式时不涉及似然函数的条件最大值，求解过程更稳定，并且显著减少了所需要的计算时间[11]。将严格稳定分布与指数倾斜相结合已经被证明在很多应用（例如：重要性采样、罕见事件的模拟、保险精算等）中非常有效。

算法2Gibbs采样过程

5 后验推理质量评估方法

对于rILFM模型而言，对观测到的网络数据和预测出的网络数据进行比较，可以看作是一个判断图相似的问题。采用基于图卷积神经网络的图分类算法来进行图的相似性比较是一种比较理想的方案，若两个图能够被分到同一个类别中，则意味着它们的表征向量是向量空间中两个相近的点，即它们具有很大的相似性。给定一组图G1,G2,…,Gn构成的集合G，和对应的一组标签y1,y2,…,yn构成的集合Y，图分类是指得到一个学习模型能够学习出整个图的表征向量hG，使得yG=g(hG)，这里g是一个由表征向量得到图标签的映射。图卷积神经网络利用图结构和结点的特征向量Xv来学习结点的表征向量hv：采用递归地对邻居结点的特征向量进行聚集的模式来得到结点的表征向量，第一层卷积对结点的直接邻居（跳数为1的邻居）进行了聚合，第二个卷积层对结点的跳数为2 的邻居进行聚合，…，经过第k个卷积层的聚集后，结点的表征向量已经充分捕获了其k跳邻居所体现的网络结构信息。整个图的表征向量hG可以通过图级别的池化层得到[15]。

对抗样本是指在数据集中通过故意引入细微的干扰所形成输入样本，引入干扰之后的输入样本会高概率得出错误输出。引入对抗样本提供了一个修正深度模型的机会，因为可以利用对抗样本来提高模型的抗干扰能力。对抗训练就是将对抗样本和正常样本一起训练，是一种有效的正则化技术，可以提高模型的准确度，同时也能有效降低对抗样本的攻击成功率。

为什么在不考虑对抗样本的情况下来训练分类器有可能会导致学习效果不好，有人怀疑是因为深度神经网络模型的非线性性，也许再加上不充分的模型平均和不充分的正则化（即过拟合）[16]。Tramer 认为这些猜测都是不必要的，相反，他认为模型在高维空间中的线性性是对抗样本存在的[17]。下面从一个线性模型入手，举例来解释对抗样本的存在性问题：在很多问题当中，一个输入的特征的取值精度通常是有限制的，这就意味着当在特征的取值上做一个微小的扰动（在精度范围内），分类器不应该返回不同的结果。比如现在有一个样本和一个对抗输入，当扰动足够小的时候，分类器对正常样本和对抗样本的响应应该是一样的。考虑一个权值向量，对抗扰动使得激发增长了。显然，可以通过加入对抗样本来使得激发增长。对于有限的k个维度，如果在每个维度上增加扰动，那么激发可以增加最大。因为与维度无关，而激发增加量随维度线性增长，那么在高维问题中，可以很大程度改变输出，但是在输入上只需要做极小的改动。这个例子说明，如果维度足够的话，一个简单的线性模型同样存在对抗样本的问题。过去对对抗样本的那些牵扯到神经网络的性质的解释，比如误认它们具有高度的非线性，可能都不对。基于线性的假设更简单，并且能够解释softmax 回归也对对抗样本很脆弱的事实。因此，基于线性，对抗样本很容易生成。

显然，需要一个在引入对抗样本的情况下依然能够得到较好的分类结果的图分类器来进行图相似性判断，Zhang等人[18]提出的图卷积神经网络框架DGCNN恰好符合本文的需求。因此，基于DGCNN训练了一个多类别的图分类器。

采用了一种两阶段样本收集策略：在第一阶段，运行了一条MCMC 链，从这条链上收集到的样本用作下一阶段的种子样本，包含三个步骤：

如果有K值的标准答案，就用这个标准答案来作为的值；否则，采用从MCMC 链收集到的样本的Ks值的众数作为的值。

（2）确定总结范围K

当确定了的值，那么总结范围就是范围跨度意味着当进行参数后验推理结果总结时，只考虑三类样本，即1 这三类样本。也可以将范围跨度的值设置成5，以保留更多的样本。

（3）选择种子样本

从MCMC 链收集到的最后几个样本中，选择三个满足Ks∈K的样本作为种子样本。

在第二阶段中，运行了三条MCMC链，以每一个种子样本作为每条链的起始位置，从每条链进行maxIter次采样，收集maxIter-burning个样本，并且令作为该条链采样出的样本的Ks真值，这样从不同链上采样到具有同一Ks值的样本，在对应真值的链上就是正样本，在其他链上就是负样本，这样就引入了对抗样本。在第二阶段中，通过以下五个步骤来准备DGCNN模型的训练数据：

（1）生成作为训练样本的图

将保留下来的样本作为参数，用提出的网络生成模型生成图结构数据。

（2）给生成的图打标签

若Ks=，则图对应的标签ys=1（正样本），否则ys=0（负样本）。

（3）重新给生成的图打标签

采用以下规则重新给生成的图打标签，若ys=1，则最终，生成的图就有了四种标签，即正样本有三类标签。

（4）为每一个图赋结点属性

社区隶属指派矩阵Zs作为结点特征向量构成的矩阵。DGCNN 模型要求结点的特征向量具有相同的长度，因此对长度不足的部分用0做了填充。

（5）将训练样本数据写入文本文件

将所有的正样本和负样本按采样顺序写入输入数据文件。图3 展示了在模拟数据上进行实验时的输入数据文件片段。

6 实验验证

6.1 在模拟数据上进行实验验证

利用所提出的生成模型产生了一个有30 个结点的计数值网络。将超参数的初始值设置为a=0.2 ，b=1，c=8，d=1/HN，e=0.5，f=0.8，λ～gamma(a,b)，p～beta(e,f)，α～gamma(e,f)，得到的实际超参数值是α=1.765 8，HN=3.994 98，λ=0.387 2，p=0.28。30个结点产生了666条连边。在第一阶段，运行了一条MCMC链，已知Kˉ=8，因此K={7,8,9}，采样得到了三个种子样本作为第二阶段运行的3 条MCMC 链（分别称之为chain1、chain2、chain3）的起始位置，对于每一条链，都设定maxIter=10 000，burning=4 000，因此从每条链收集到6 000个样本。表1列出了从每条链收集到的样本中Ks取值的分布，Ks的取值范围是整数区间[4，14]，3条链的众数都是Ks=8。

图3 在模拟数据上进行实验时的输入数据文件片段

表1 从3条链收集到的样本中，Ks 值的分布情况

表2 在测试数据上，训练样本的标签分布情况

为了保持各类别的样本均衡[19]，随机扔掉了一些负样本。表2 中最后一列是保留下的负样本数。生成了5 768个训练样本，其中有2 072个图的类标签是ys=8，1 022 个图的类标签是ys=9 ，1 311 个图的类标签是ys=7，1 433 个图的类标签是ys=0。相应地，有5 840个测试样本。

表3 记录了图分类器在测试数据上的部分预测结果。可以看到在第1回合结束后，训练准确率是tAcc=0.431 6，所有5 840 个测试样本都被错分了。Go和Gp预测出的分类标签都是0（表示没有被分到标签ys=7或ys=8 或ys=9 的任何一个类中）；从第275 个回合开始，训练准确率便达到99%，测试准确率达到0.93，四个类中都只有少量测试样本被错分，由此可见训练出的图分类器能够比较准确地对测试数据进行分类。

表3 图分类器在测试数据上的部分预测结果

图4 展示了图分类器在模拟数据集上的实际运行结果，其中图（a）通过折线图的方式展现了在每个训练测试回合中测试数据被正确分类和错误分类的样本个数；图（b）通过折线图的方式展现了每个训练测试回合中训练数据集上的准确率、损失函数值和曲线下的面积；图（c）通过折线图的方式展现了在图深度神经网络的每个训练测试回合中落入标签ys=7 或ys=8 或ys=9 的任何一个类中的样本个数以及未被正确分类的样本个数。

6.2 在真实网络数据上进行实验验证

LESMIS 网络是由 D.Knuth 于 1993 年整理出的，描述了维克多·雨果的著作《悲惨世界》中的人物共现关系。在第一阶段选择从MCMC链（令超参初始值a=0.2，b=1，c=8，d=1/HN，e=0.5，f=0.8，λ～gamma(a,b)，p～beta(e,f)，α～gamma(e,f)）采样到样本的Ks值的众数Ks=15 作为的值，因此K={14,15,16}。得到了三个种子样本作为第二阶段运行的3条MCMC链（分别称之为chain1、chain2、chain3）的起始位置，从每条链收集到5 000个样本。如表4所示，Ks的取值范围是整数区间[13，19]，3条链的众数都是Ks=15。

依据样本收集策略，保留了满足条件的样本，并以这些样本作为参数，通过生成模型生成图，依据图标签策略为这些图打标签（如表5所示）。

为了保持各类别的样本均衡，随机扔掉了一些负样本，表5中最后一列是保留下的负样本数。生成了5 751个训练样本，其中有1 284 个图的类标签是ys=14，2 020 个图的类标签是ys=15，1 206 个图的类标签是ys=16，1 241个图的类标签是ys=0。相应地，有5 753个训练样本，图5展示了在真实数据上进行实验的输入数据文件片段。

图4 图分类器在模拟数据集上的运行结果

表4 从两条链收集到的样本的Ks 取值的出现频次

表5 在真实数据上，训练样本的标签分布情况

在真实网络数据上进行实验时，有5 753 个测试样本。表6 记录了图分类器在测试数据上的部分预测结果。可以看到在第1回合结束后，训练准确率是tAcc=0.428 9，所有5 753个测试样本都被错分了，Go和Gp预测出的分类标签都是0（表示没有被分到标签ys=14 或ys=15 或ys=16 的任何一个类中）；从第278 个回合开始，训练准确率变成99%，测试准确率达到0.923。

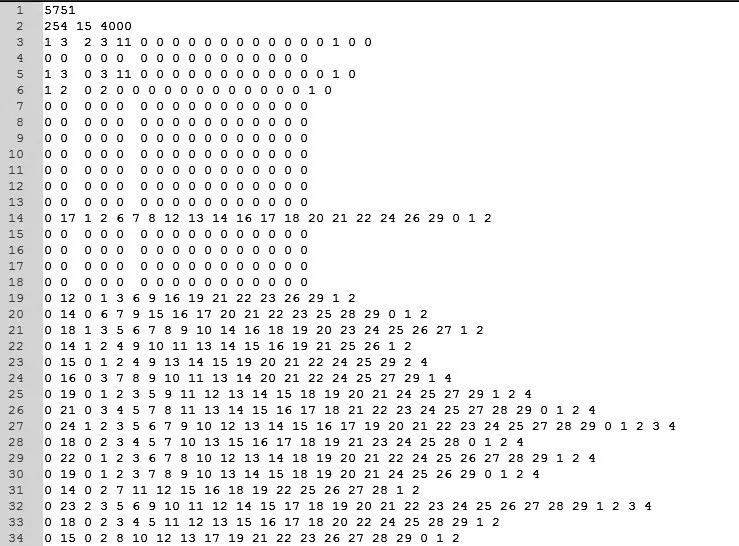
图5 在真实数据上进行实验时的输入数据文件片段

图6展示了测试分类预测结果的内容片段，可以看到在第104 个回合，预测出Go的分类标签是ys=0，预测出Gp的分类标签是ys=15，测试样本有1 124 个被分类到ys=14，有1 754个被分类到ys=15，有1 012个被分类到ys=16，有505 个被分类到ys=0，有1 358 个没有被准确分类，列出了没有被准确分类的样本。

表6 图分类器在真实数据上的部分预测结果

图7 展示了图分类器在真实数据集上的实际运行结果，图（a）通过折线图的方式展现了在每个训练测试回合中测试数据被正确分类和错误分类的样本个数；图（b）通过折线图的方式展现了每个训练测试回合中训练数据集上的准确率、损失函数值和曲线下的面积；图（c）通过折线图的方式展现了在图深度神经网络的每个训练测试回合中落入标签ys=14 或ys=15 或ys=16 的任何一个类中的样本个数。

7 结束语

在没有引入对抗样本的情况下来训练图分类器的时候，图卷积网络的训练准确率和测试准确率都会快速达到0.99 以上，然而当继续增加训练回合时，发现分类器的测试准确率会忽上忽下，极不稳定。引入了对抗样本后，尽管图卷积网络的训练准确率和测试准确率需要很多回合后才能达到0.99 以上，但是当继续增加训练回合时，会发现分类器的测试准确率一直是稳定提升的。

图6 图分类器在真实数据集上的测试分类预测结果片段

图7 图分类器在真实数据集上的运行结果

当采用只有图结构没有结点属性矩阵的训练数据来训练图分类器，结果将变得非常差，训练准确率始终在40%至50%之间徘徊，即使训练150 个回合后，训练准确率也没有超过51%。这样的结果是可以理解的，因为只有图结构信息，没有结点特征信息，无法让深度图卷积神经网络计算出结点的结构角色，从另外一个侧面证明了社区结构的重要性。