基于区块链技术的产品供应链信息追溯研究*

□ 赵俊丽，冉文学

(云南财经大学 物流学院，云南 昆明 650221)

1 前言

供应链是指在一个产品销售网络中将产品经由供应商、制造商、经销商流通到最终消费者手中的一个网链结构。产品溯源是指通过现在先进的物联网、互联网、自动识别技术等对产品在整个供应链中的流通过程进行追踪。现今社会，随着消费者对高品质生活的追求，产品是否安全和假冒伪劣品成为广大消费者高度关注的问题。因此，基于区块链技术对产品供应链信息进行追溯有着重要的研究意义。

供应链物流的运营效率可以通过区块链技术得到有效的提升，秦明[1]分析了现阶段供应链物流的发展情况，根据区块链与供应链物流管理的相适性，提出了推动供应链物流持续发展的相关建议；谢思宇等[2]分析了价格昂贵产品的供应链各个环节的可追溯性问题，开发出了基于区块链技术的高价产品的可追溯交易平台，以期更好地保障消费者的合法权益；上官璐洁[3]分析了当前阶段区块链技术在各个不同领域的应用，认为很多方面并不是很成熟，进而引发了对区块链技术优化与应用的研究。区块链技术的去中心化、可溯源性、不可篡改等特性可以改变传统供应链管理中信息不对称、难以溯源查责、信任机制不健全等问题[4]；许重建等[5]首先对现有区块链交易数据隐私保护进行研究，然后对数据隐私保护需求进行定性分析，建立相关矩阵，来探究区块链交易数据隐私保护的方法。在现今这个互联网高度发达的社会，信息的真实性、可追溯性、隐秘性成为一个热点问题。

区块链因为其可以实现信息流、资金流、物流等各个要素的去中心化自由流通的特性，因此，可以在溯源领域中广泛应用[6]。贾丰涛等[7]利用区块链技术的去中心化、加密性等特点，将其与农产品物流体系相结合，以保证产品的可追溯性和安全性；谢思宇等[8]分析了家具信息追溯在整个供应链条上存在的问题，为了家具的质量能够得到及时地监控和跟踪，作者运用区块链技术建立了家具的电子商务溯源系统；张文超等[9]为了使药品追溯问题得到解决也运用到了区块链相关技术；蔡明等[10]赋予供应链上所产生的交易数据以非同质化的token，以此保障数据的可追溯性和不可篡改性，旨在保障资金安全与商品防伪。

综上所述，本文是将区块链技术应用到产品的供应链上，不需要在产品上再附加条形码、二维码等电子标签就可以实现对产品供应链信息的追溯。主要内容是，由品牌贴牌商在区块链上发行代表某产品的虚拟货币，在商品流通网络中，上一级的交易者在将产品交付给下一级交易者的时候，可以自由选择是否将代表某产品的同等数量的虚拟货币交付给下一级的交易者，将足够长时间内的虚拟货币流通情况收集起来，然后根据收集到的相关信息建立数学模型，据此计算出从商品流通网络中任意经销商处获得的某个产品来自品牌商的概率即产品的正品率。根据这些计算得出的概率，可以实现产品的相对溯源，结合网络信息便可以实现对产品的绝对溯源。

2 问题描述

产品供应链是指制造商制造一件产品经过一系列流通过程到达消费者手中的各个环节所构成的流通链条。一个产品从生产者到达消费者大致要经过如下图1所示的几个过程，制造商将产品制造出来，经过以下的几个环节可以到达消费者手中，在这个过程中，制造商、分销商和消费者可以有多个，但是品牌商只有一个。品牌商需要对产品的质量、后续服务等负责，品牌商是这个产品流通链条的重要一环。消费者从任一分销商处所获得的产品有多大概率是来自该品牌的商品是本文所要研究的问题。

图1 产品流通链

为了实现对产品的相对溯源，需要对产品流通链条中的各个过程进行记录。本文便是利用区块链这一技术来完成这一任务。区块链技术中的区块就类似于计算机中的硬盘，这些硬盘将所有的信息存储起来，再通过计算机编码等技术对存储起来的信息进行加密，这些信息的真实性与可靠性就得到了保证。由于区块链的这一技术特性，其被广泛应用。虚拟货币是一种不需要由特别指定的货币机构发行的一种P2P形式的数字代币，这种代币可以运用特别的算法、经由复杂的计算所得，并通过P2P网络来记录整个交易行为以及交易数据，同时，使用计算机编码设置密码来使虚拟货币在流通网络中的安全得到保障。本文运用一种虚拟货币来记录某产品供应链流通过程中的相关情况，即买方在向卖方购买产品的时候，卖方可以决定是否将代表相等数量产品的虚拟货币交付给买家。当卖家将一定数量的虚拟货币交付给买家的时候，该交易的数据便被记录了下来。

现在假设某一产品，市场上存在n个交易者(N1,N2,…,Nn)来对某产品进行交易。在这一交易网络中，N1是产品虚拟货币的发行者，也就是品牌商。经过足够长一段时间后，可以从区块链中检索得到一段时间内交易者Ni(i=2,3,…,n)从交易者Nj=(j=1,2,…,n)处得到的产品虚拟货币的数量wij，根据这些数据可以得到一段时间内产品的流通矩阵

(1)

在产品流通矩阵中，因为wii代表自己与自己的交易数量，并没有实际的意义，故wii=0(i=2,3,…,n)。本文所研究的问题是基于交易者的随机发货，消费者从任意一个交易者出处购买某一产品，求其有多大的概率是来自品牌商N1。

3 模型构建

令Pi表示本文研究所要求解的概率，亦即从任意交易者处得到的产品来自品牌商N1的概率。接下来求Pi。首先，通过检索区块链信息来构建某一段足够长时间内的产品流通矩阵。比如，假设市场上存在7个交易者来交易某一产品，可以形成针对该产品的交易网络。如图2所示，是某一产品的流通网络示意图。以交易者N2为例，N1指向N2的箭头表示交易N2者从交易者N1处购买产品，N1指向N2的数字代表交易者N1交给交易者N2的代表同等数量产品的虚拟货币，即w21=30；同样地，N2指向N4的数字代表交易者N2交给交易者N4的代表同等数量产品的虚拟货币，即w42=26。

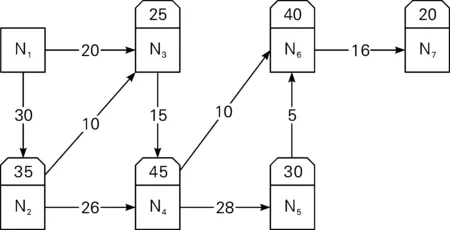
图2 产品流通网络示意图

设qij表示交易者Ni(i=2,3,…,n)的直接上游交易者将任意一件产品交给该交易者的概率。直接上游交易者是与上游交易者相对的，直接上游交易者表示一段时间内该交易者向某交易者交付了代表产品数量的虚拟货币。如图2所示，交易者N3向交易者N4交付了虚拟货币，则称交易者N3是交易者N4的直接上游交易者；交易者N3并没有向交易者N5交付虚拟货币，则N3不是N5的直接上游交易者。可以说交易者N1是除其本身以外的所有交易者的上游交易者，因为交易者N1是产品虚拟货币的发行者。

(2)

(3)

由此可以得到Pi与qij的关系为：

(4)

在以上方程组中，由于P1表示的是产品直接来自品牌商，所以P1=1。当产品不是直接来自品牌商时，消费者获得的产品有多大的概率来自品牌商这一问题便转化为求解方程组的问题。假设矩阵

P=A×P+α

(5)

如果

(6)

此时，可以使用一阶定常迭代法求解上述线性方程组有且仅有一组解，递推公式为：

P(i+1)=A×P(i)+α

(7)

其中P(i)表示第l次迭代求得的解。若想要证明方程组(4)的存在并求得其解，只需要证明(6)式成立。下面首先要对一种特殊的有向图的性质进行分析探讨。

概念1 假设有向图G=(D,B)，其中顶点集合D为非空集合，D={D1,D2,…,Dn}，B称为弧集，弧的条数|B|=k，则有向图G满足以下的条件：

①D1可以到达除了自身以外所有的顶点，即D1可以到达∀Dj∈{D2,D3,…,Dn}。

②不存在连接某个顶点自身的弧。

③不存在反向弧λ(〈Di,Dj〉)，即不存在其他顶点到达顶点D1的弧。

④假设λ(〈Di,Dj〉)是有向弧的权值，当λ(〈Di,Dj〉)=0时表示有向弧不存在，易知有向弧不存在时，λ(〈Di,Dj〉)=0。对于∀Di,Dj(i,j∈N+,i,j≤n)，λ(〈Di,Dj〉)满足以下条件：

(8)

概念2 令f代表顶点Di到顶点Dj的一条通路，Bf代表通路包含的所有弧的集合，将这条通路上所有权值的积称为这条通路的积，即Ω(f)=∏b∈Bfλ(b)。当i与j相等时，顶点Di到顶点Dj形成一条环，称Ω(f)是这条环的积。

定理1 图G中的任意一个环均有0<Ω(f)<1。

下面来证明上述定理1。

假设图G中的一个环是f=d0b1d1b2,…,b1dlb0d0，其中d0,d1,…,dk,d0表示环f依次经过的顶点，b1,b2,…,bl,b0表示环f依次经过的弧。令D′={d0,d1,…,dl}，B′={b0,b1,…,bl}。根据公式(8)可得bi弧的权值λ(bi)满足

0≤λ(bi)≤1，i=0,1,2,…,l

(9)

根据概念2可知，环f的积为：

(10)

由公式(9)和(10)可知环的积满足以下条件：

0<Ω(f)≤1

(11)

环f的积不等于0的原因是因为不可能有一条弧的权值为0。

接下来需要证明Ω(f)≠1的情况。假设图G中存在环的积为1的情况，即当Ω(f)=1时，根据公式(10)和(11)可得：

λ(bi)=1,i=0,1,2,…,l

(12)

假设在环f以外存在另外一个顶点d连接到顶点di(di∈D′)，并且易知λ(〈d,di〉)，结合公式(12)可得：

λ(bi)+λ(〈b,bi〉)>1,i=0,1,2,…,l

(13)

(14)

在上述矩T阵中，

(15)

概念4 令F(l)(di,dj)代表顶点di到顶点dj经过l条弧的通路的集合。现在将通路集合中所有通路的积的和称为这条通路集合的积，记作∏F(l)(di,dj)，也即∏F(l)(di,dj)=∑m∈F(l)(di,dj)Ω(f)。同理可得∏F(l)(di,dj)代表所有环F(l)(di,dj)之积。

下面来证明上述定理：

假设当l=v(v≥2)时原式成立，即

(16)

(17)

根据公式(16)、(17)和概念3可知：

(18)

(19)

(20)

接下来需要证明

(21)

假设从顶点di到顶点dj经过了v+1条弧，并且ds为通过的倒数第二个顶点，由这些通路所组成的集合表示为F(v+1)(di,dj|ds)。 根据概念4可得：

∏F(v+1)(di,dj|ds)=∏F(v)(di,ds)·λ(〈ds,dj〉)

(22)

(23)

(24)

假设对于任意的f(l)∈F(l)(di,dj)，令f(l)代表经过顶点di到dj所通过l条边的通路。有向图G中的顶点数为|D|=n，当l>n时，所经过的通路中一定包括一个环。假设该环为h(z)，z代表这个环经过的弧的条数，将该环循环一次可以得到顶点di到dj所通过l+z条边的通路，即f(l+z)∈F(l+z)(di,dj)；同样，将该环循环m次可以得到顶点di到dj所通过l+m·z条边的通路，也即f(l+m·z)∈F(l+m·z)(di,dj)。根据概念2可以得到：

Ω(f(l+m·z))=Ω(f(l))·[Ω(h)(z)]m

(25)

由上式可得：

(26)

又因为

0<Ω(f(l))<1

(27)

0<Ω(h(z))<1

(28)

所以

(29)

根据概念4可得：

(30)

证明：产品流通网络中的n个交易者可以被看作是有向图G1=〈D1,B1〉中的n个顶点，则D1={N1,N2,…,Nn}，那么顶点Ni到顶点Nj的权重值可以表示为

(31)

4 算例分析

如图3所示，是一段足够长时间内某一特定产品的网络流通图，根据前文中的描述，N1代表该品牌的品牌商，N2,N3,N4,…,N28代表该产品的任意经销商或者购买商，有向弧〈Nj,Ni〉上所示的权重代表wij，Ni上多边形中的数字代表Wi。如图3所示，现在以交易者N2为例，有向弧〈N2,N14〉边上的权重值代表一段时间内交易者N2向交易者N14交付产品的虚拟货币的数量w14,2=15；而N2上方的多边形中数字代表交易者N2总的进货量为W2=30。根据图3所表达的信息以及前文中所描述的方法，可以得到相应的货币流通矩阵w以及中间商进货的总量矩阵W。

图3 产品流通网络图

令P(0)=(0,0,…,0)T，运用公式(7)中所描述的一阶定常迭代法迭代24次可求得P24；不运用迭代法求解得到的最优解为P′。P24、P′如下：

由上述最优解P24和P′的值易知max{|P′-P24|}<0.001，所以运用一阶定常迭代法求得的最优解是合理的。之所以用一阶定常迭代法来求解是因为相比较传统求解方法来说，这种方法可以很大程度上减少运算步骤，提高求解效率。

以上的求解方法中，根据产品流通网络，通过检索区块链信息可以得到wij，但是对Wi估计的准确程度对Pi值的精确性有直接的影响。又因为Wi是进货量，是一个企业中比较隐私的问题，很少有企业愿意将真实的信息发布出去，接下来所描述的方法可以让企业或者交易者发布较为可靠的进货量数据Wi。

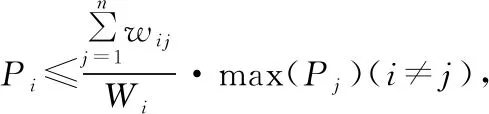
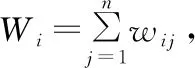
5 结束语

在现今社会，人们对品质有着更高的追求，因此，本文所探究的问题在一定程度上为消费者购买产品的品质提供了保障。本文所研究的方法相对于现在社会上已有的二维码、条码等实施的难度比较低，而且成本小，适用产品的范围也比较广，例如，一个很小的生活用品，牙刷、牙膏之类的，如果去运用RFID等之类的技术，无疑是增加了产品成本。

企业可以运用本文所研究的方法对相关产品实现溯源，保证产品在流通网络中正品的概率。因为虚拟货币具有不可伪造、不可篡改等特性，所以，运用该方法对产品进行的溯源更具有真实可靠性。此外，在区块链中所存储的产品的流通交易数据，也可以为企业和政府在进行分析决策时提供有意义的帮助。

本文基于区块链技术对产品供应链的信息进行溯源也存在一定的缺陷。在进行溯源的开始阶段，会由于信息不对称等各种原因造成溯源的效果不太好。但是随着市场环境的改善以及在网络的协同作用下，是可以实现对产品的绝对溯源的。本文所研究的方法适合于市场价格比较稳定的产品，也就是说适合于在一个完全竞争的市场上所交易的产品。本文所研究的方法与现在社会上已有的溯源方法并不冲突，与此同时，在区块链上所搜集的信息还可以为其他的溯源方法所运用。