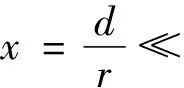同心球壳电容器与同轴圆筒电容器的对应性

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

对于球形电容器和圆柱形电容器，由于带电球面或带电圆筒在其内部空间产生的场强为零，则内极板包围的区域没有电场；由于两极表面的等量异种电荷都等效于集中在球心或轴线上而相互中和，则外极板之外的区域没有电场.所以只在两极板之间存在电场，或者说，电容器内部电场相当于只由里面的电极产生，与外面的电极无关.而且两种电容器的电容公式和优化设计半径的尺寸都具有对应性.

1 电容器的尺寸设计

【例1】[1]两个同心导体球壳，外球壳的内半径R=5 cm，内球壳的外半径可以任意选择，若两球壳之间充满各向同性均匀电介质，能使该电介质恰好不被击穿的电场强度为2×107V/m，试求两球壳之间能承受的最大电压.

解析:设内球壳的外半径为r，内、外球壳的电荷量分别为Q，-Q，相对介电常数为εr，以圆心为坐标原点，则两球壳之间的场强与坐标x的关系式为

可知两球壳之间的电势差为

由场强的关系式可知，当x=r时，Ex取最大值，而Ex的允许最大值为Em，则

【例2】[2]由绝缘介质隔开的两个同轴的柱形导体构成了同轴柱形电容器.设内、外导体与介质接触面的半径分别为r和R，长度为l(l≫R-r)，两圆筒之间充满相对介电常数为εr的电介质，其击穿场强为Emax.在外半径R一定的情况下，为使电容器能够承受的电压最大，求内圆柱导体的半径r应为多大.

解析:真空中均匀带电无限长直线在距离为x处的场强大小为

设圆筒电容器内、外两极分别带等量正、负电荷，那么只有在两圆筒之间的区域存在电场，这相当于只由里面的圆筒产生电场，而均匀带电无限长圆筒在圆筒外面产生的电场可等效为电荷集中于圆筒轴线上的均匀带电的无限长直线产生的电场，可知介质中离轴线x处的场强为

(1)

电容器内、外圆筒之间的电势差为

(2)

由式(1)可知，当x=r时，场强最大，而电介质其击穿场强为Emax，代入式(2)得

(3)

则

所以当内圆柱导体的半径r=0.368R时，可使设计出的电容器能够承受的电压最大.

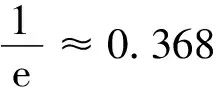
2 电容器的电容公式

【例3】试推导同心球壳电容器的电容公式.

解析:两球壳之间的电势差为

可知电容的倒数为

所以电容为

由此可知球壳电容器两极等效正对面积等于两个球壳表面积的几何平均数.

【例4】试推导同轴圆筒电容器的电容公式.

解析:同心圆筒电容器两极的电势差为

所以电容为