数学焦虑对初中生概率推理的影响——一个有调节的中介模型

史滋福，谢云天

数学焦虑对初中生概率推理的影响——一个有调节的中介模型

史滋福，谢云天

（湖南师范大学 心理学系 认知与人类行为湖南省重点实验室，湖南 长沙 410081）

采用数学焦虑量表、概率推理量表以及数学元认知问卷对431名初中生进行测查，探讨数学焦虑对初中生概率推理的影响及作用机制．结果发现：（1）数学元认知在数学焦虑与概率推理之间起中介作用；（2）数学元认知知识在数学焦虑与概率推理之间的中介作用不显著；（3）数学元认知体验、数学元认知监控在数学焦虑和概率推理之间起中介作用；（4）性别调节了数学焦虑经过数学元认知监控对概率推理的中介效应．与男生相比，女生数学焦虑经过数学元认知监控对概率推理的中介效应显著增加．因此，数学焦虑和初中生概率推理之间存在有调节的中介效应．

概率推理；数学焦虑；数学元认知；性别

1 问题提出

人们在日常生活中常常遇到不确定性事件．随着年龄的增长，基于不确定事件的概率判断变得越来越重要[1]．目前，统计与概率是中国义务教育阶段数学学习的主要内容之一．《义务教育数学课程标准（2011年版）》明确指出：“推理的发展应贯穿于整个数学学习过程中．”虽然计算比率的能力较早开始发展，但有关概率推理的相关规则大多是在青春期获得的[2]．对于正处于青春期的初中生来说，他们在这个时期形成、发展的概率推理能力很可能影响他们在学习、生活中的判断和决策，影响今后的成长．因此，关注初中生的概率推理能力及其影响具有重要的现实意义．

纵观以往研究，有研究认为，成年人经常违反概率论中的某些重要规则[3]．儿童在概率推理中也表现出成人文献中的偏向[4]．也有研究认为，儿童倾向于退回到主观判断，其概率思维倾向于“过渡性”（transitional）或“非正式的定量”（informal quantitative）推理[5]．事实上，人们通常对随机性和概率持有正确和不正确的直觉和信念，其中有些会导致人们做出有偏向的推理[6]．为了消除这些不合理信念的影响，研究者大多从“问题表征”及“认知能力”、“认知负荷”以及“思维风格”等对成人概率推理的影响进行探讨[7–8]．但概率推理问题大多以数学问题的形式出现，在一定程度上可能受到数学焦虑这种消极情绪的影响，妨碍人们的思维，阻碍和掩盖真实的概率推理表现[9]．加工效能理论也认为，焦虑会导致可利用的资源相对减少，从而降低个体认知活动的加工效能[10]．已有研究表明，数学焦虑和数学成绩呈负相关，高数学焦虑学生的数学成绩显著更低[11]．Primi等（2017）[12]的研究也发现，数学焦虑和概率推理显著负相关，高数学焦虑个体的概率推理能力相对较低．

近来，抑制型焦虑模型理论对数学领域的现象做出了解释，认为数学焦虑通过影响信息的预加工、加工和检索，占用元认知资源，从而降低个体的数学表现[13]．数学元认知在数学焦虑与数学学业成就之间起中介作用[14–15]．高焦虑的个体更少运用调节性策略[16]．一项纳入了118篇文章、149个独立样本的元分析结果显示，元认知在控制智力的同时也能预测学业成绩[17]．这说明了元认知对学业成绩的重要影响．而概率推理问题一方面有数学问题的特征，另一方面，元认知在青春期中期开始影响推理表现，它可以抑制启发式偏向，使推理者对备择答案做出考虑，从而减少依赖启发式和直觉反应的倾向[18]，而且高年级儿童表现得更好[19]．基于此，提出假设H1：数学元认知在数学焦虑与概率推理之间具有中介作用．另外，数学元认知包括3个成分，即数学元认知知识、数学元认知体验以及数学元认知监控[20]．这3个成分对高效率数学学习学生的数学成绩均有直接影响[21]．但由于其作用不同，如元认知知识具有奠基作用[22]，元认知体验具有推动作用[23]，而作为核心内容的元认知监控通过元认知知识和元认知体验的交互作用实现其作用[20]．因此，进一步提出假设H2：数学元认知知识、数学元认知体验、数学元认知监控在中介数学焦虑与概率推理之间关系的作用不一样．

性别差异是人类最基本的自然差别和社会角色差别之一[24]．信息加工理论认为，个体对认知信息的加工存在差异<[25–26]．男性和女性的信息加工模式不同[27]．即使处理相同的认知信息，也会产生不同的结果．概率推理中的个体差异不仅与元认知有关，还与认知能力有关，认知能力在识别相关信息以避免错误直觉和启发式反应方面发挥着重要作用[4]．与初中男生相比，初中女生的形式抽象能力和运算推理能力更突出[28]．因而，即使元认知水平相同，但因为受到认知能力等因素的影响，男性和女性的概率推理表现也可能存在差异．再加上，元认知活动涉及确定方向、做出规划、开展评估等部分[29–30]．有研究显示，性别可以显著调节个人规划对学业成绩的影响[31]．那么，在应用数学元认知资源来解决概率推理问题的过程中，是否会因为男女生信息加工模式的不一样而导致不同的结果呢？更何况，女性在处理任何类型的信息时都可能更有反思性[32]．与男生相比，女生的数学元认知对概率推理的影响可能更为显著．据此提出假设H3：性别的调节作用发生在中介的后半路径，即性别显著调节数学元认知对概率推理的影响，且女生数学元认知对概率推理的影响更大（见图1）．

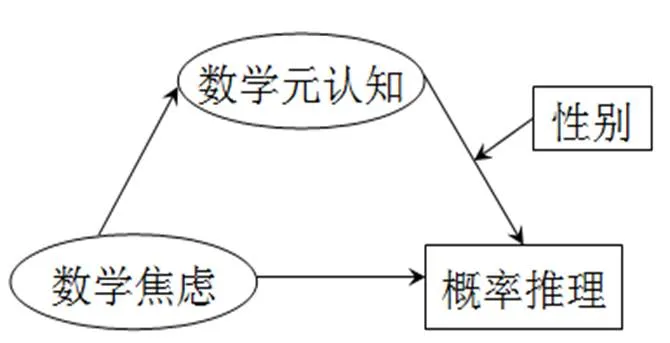
图1 有调节的中介模型概念

综上，研究目的主要有两个：其一，考察数学元认知（数学元认知知识、数学元认知体验、数学元认知监控）对数学焦虑和概率推理的关系是否具有中介作用；其二，考察性别对该中介作用是否具有调节效应．该模型对揭示初中生理解和解释日常生活情境中的概率信息，顺利完成对随机事件的推理，抵御一些推理中的典型谬误和偏见，并能完成入门统计课程所需要的基本概率推理能力所存在的问题具有重要的意义，也有助于识别统计教育领域中推理困难的学生和推理困难的原因，使其从课程一开始就得到教育支持，帮助其日后理性决策和不确定性判断．

2 方法

2.1 被试

采用方便取样法，选取湖南省长沙市某中学431名初中生为被试．其中，男生214人（49.65%），女生217人（50.35%）；初一156人（36.19%），初二140人（32.48%），初三135人（31.32%）；平均年龄为13.02岁（=0.96，年龄范围为11~16岁）．已有的研究表明年级影响个体的元认知[33]和推理水平[34–35]，因此，研究中除了收集性别方面的信息，也收集了年级方面的信息．

2.2 研究工具

2.2.1 概率推理量表

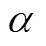
2.2.2 数学焦虑量表

2.2.3 数学元认知问卷

2.3 程序及数据处理

研究者于2018年下半年期中考试前期，在所选取的中学里利用上课时间，以班级为单位进行团体施测．在学生填答前，由主试说明调查目的和注意事项，要求学生认真、独立地回答每一道题目．所有问卷当场回收．采用SPSS23.0和MPLUS7.4对数据进行统计分析．

3 结果

3.1 共同方法偏差

在收集数据过程中，通过部分条目反向计分等方法对共同方法偏差进行程序控制．数据收集完成后，采用Harman单因子分析方法来检验共同方法偏差．结果发现，特征值大于1的因子共12个，第一个因子解释的变异28.94%，小于40%．这表明研究中不存在严重的共同方法偏差．

3.2 各变量的“均值”“标准差”及“相关矩阵”

各变量的均值和标准差如表1所示．在控制性别、年级影响后，相关分析结果显示，初中生概率推理和数学焦虑显著负相关，和数学元认知、数学元认知知识、数学元认知体验、数学元认知监控显著正相关；初中生数学焦虑和数学元认知、数学元认知知识、数学元认知体验、数学元认知监控显著负相关；初中生数学元认知和数学元认知知识、数学元认知体验、数学元认知监控两两之间均呈现显著正相关．

表1 描述性统计结果和变量间的偏相关分析

注：**<0.01，***<0.001

3.3 概率推理与数学焦虑及数学元认知在性别和年级上的差异比较

对不同年级男、女生的概率推理水平、数学焦虑水平及数学元认知水平进行分析发现（见图2），随着年级的提高，男生的概率推理水平和数学元认知水平先降后升，而女生的概率推理水平、数学元认知水平一直处于上升趋势；男生的数学焦虑水平先降后升，而女生的数学焦虑水平先升后降．

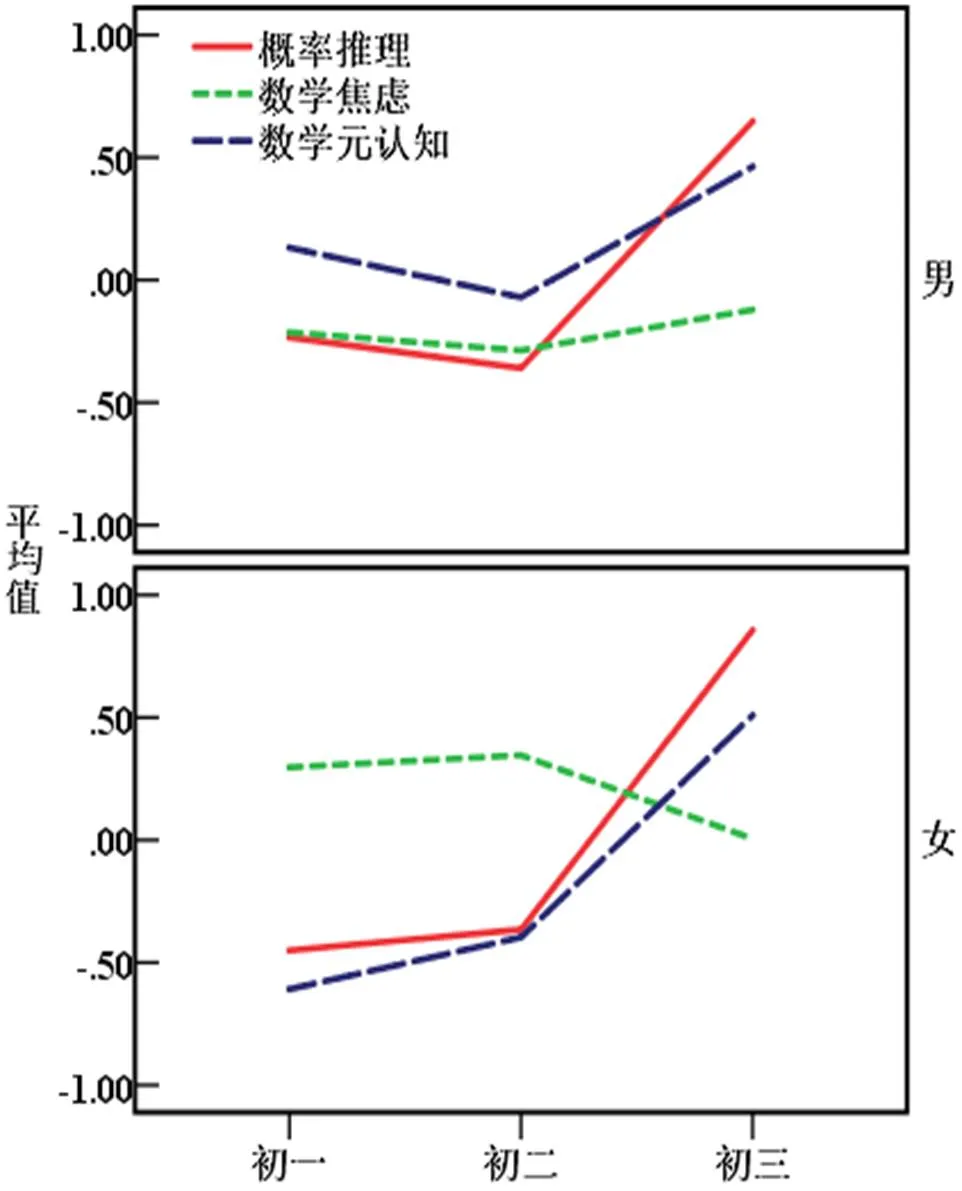
图2 男生和女生在不同年级上的概率推理与数学焦虑及数学元认知的变化特点

3.4 有调节的中介作用检验

在对每个预测变量进行了标准化处理后，所有预测变量的方差膨胀因子均低于2.39，因此不存在多重共线性问题．此外，和已有研究发现[33–35]一致，同时也发现年级影响概率推理水平和数学元认知，所以在检验有调节的中介作用时，控制了年级变量的影响．

根据方杰、温忠麟（2018）[38]提出的基于结构方程模型的有调节的中介效应分析步骤，检验性别在数学元认知中介数学焦虑和概率推理关系中的调节作用．首先，判断基准模型是否可以接受．基准模型的检验结果显示，数学元认知的中介效应值为–0.26，Bootrap95%为[–0.34, –0.19]，不包括0，说明中介效应显著．主要拟合指数为：2/=14.27，=0.83，=0.75，=0.18，=0.13．这说明基准模型拟合不好，故不接受基准模型，停止后面的步骤．

然后，分别考察数学元认知知识、数学元认知体验、数学元认知监控在数学焦虑和概率推理之间的中介作用以及性别的调节作用．

第一，检验性别在数学元认知知识中介数学焦虑和概率推理关系中的调节作用．首先，判断基准模型是否可以接受．基准模型的检验结果显示，数学元认知知识的中介效应值为–0.01，Bootstrap95%为[–0.04, 0.02]，包括0，说明中介效应不显著．主要拟合指数为：2/=12.60，=0.89，=0.81，=0.16，=0.08．这说明基准模型拟合不好，故不接受基准模型，停止后面的步骤．

第二，检验性别在数学元认知体验中介数学焦虑和概率推理关系中的调节作用．首先，判断基准模型是否可以接受．基准模型的检验结果显示，数学元认知体验的中介效应值为–0.08，Bootstrap95%为[–0.12, –0.05]，不包括0，说明中介效应显著．主要拟合指数为：2/=9.12，=0.92，=0.86，=0.14，=0.07．拟合指数说明基准模型拟合不好，故不接受基准模型，停止后面的步骤．

第三，考察性别在数学元认知监控中介数学焦虑和概率推理关系中的调节作用．步骤一，判断基准模型是否可以接受．基准模型的检验结果显示，数学元认知监控的中介效应值为–0.16，Bootstrap95%为[–0.24, –0.09]，不包括0，说明中介效应显著．主要拟合指数为：2/=8.55，=0.94，=0.90，=0.07，=0.06．这说明基准模型拟合较好，故接受基准模型，继续后面的步骤．步骤二，判断有调节的中介模型是否可以接受．结果显示，有调节的中介模型=15 513.27，相比基准模型（15 516.15），减少了2.88，表明有调节的中介模型相比基准模型有改善．步骤三，进行Bootstrap置信区间检验．结果显示，13的置信区间为[–0.09, –0.03]，不包括0．根据系数乘积法可知，数学焦虑经过数学元认知监控对概率推理的中介效应受到性别的调节．中介效应为

1(1+3)=–0.21×(0.73–0.28)=–0.15+0.06，

随变化．当=0（“0”为女）时，数学元认知监控的中介效应值为–0.15，Bootstrap95%为[–0.29, –0.09]，不包括0，中介效应显著；当=1（“1”为男），数学元认知监控的中介效应值为–0.09，Bootstrap95%为[–0.19, –0.02]，不包括0，中介效应显著．以上结果表明，与男生相比，女生数学焦虑经过数学元认知监控对概率推理的中介效应显著增加，即性别显著调节了中介效应的大小（见图3）．

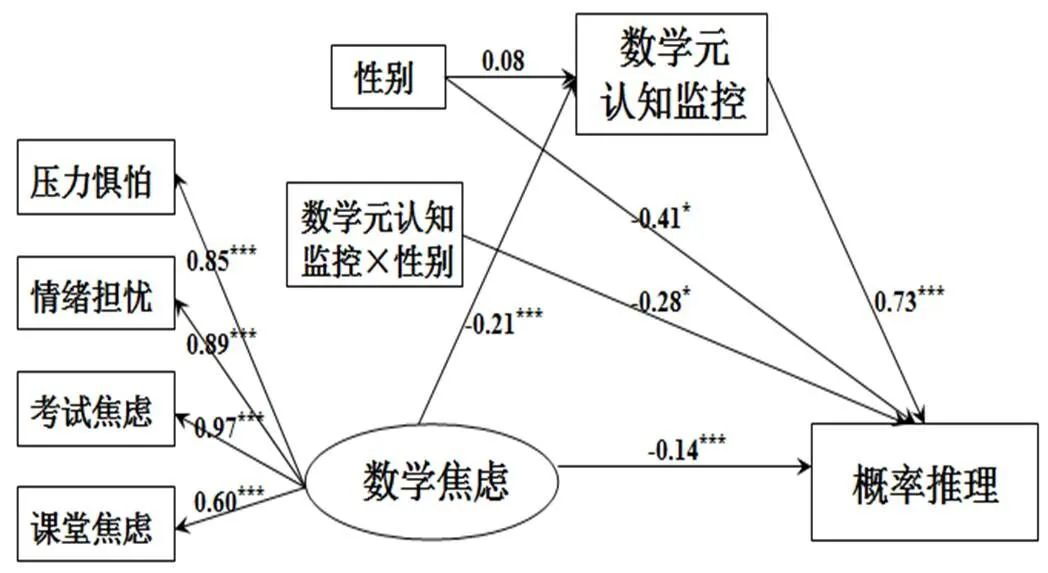
图3 有调节的中介模型路径

4 讨论

消极的感觉和紧张的情况会在不同程度上影响数学任务的成功[39]．研究发现，数学焦虑和概率推理显著负相关，且负向预测概率推理，即数学焦虑水平越高，概率推理能力越差．这与Primi等（2017）[12]的研究发现一致，也验证了加工效能理论．当个体认为认知任务存在困难的时候，焦虑对加工效能的影响会非常明显[40]．随着概率问题变得越来越复杂，给学生带来的推理任务也可能变得更加复杂[41]．许多初中生对包括概率问题在内的数学问题感到头疼、吃力，容易产生焦虑等消极情绪．由于担心负面后果而增加的焦虑会加重个体的执行资源负担，降低策略使用的效率，从而导致较差的数学表现[42]．因此，为了提升青少年的概率推理水平，引导他们缓解数学焦虑，以平和的心态看待数学问题是一个值得深入探讨的话题．

数学元认知在数学认知过程中具有重要作用[23]．研究发现，数学焦虑可以通过数学元认知对概率推理起作用，数学元认知在数学焦虑与概率推理关系中起完全中介作用．这一结果既验证了研究的假设H1，也进一步拓宽了抑制型焦虑模型的适用范围．该模型既是数学元认知在数学焦虑和数学成绩之间起中介作用的理论依据[15]，也可以用于解释数学元认知中介数学焦虑和概率推理之间的关系．当个体处于高数学焦虑状态的时候，其数学元认知资源被占用，难以为个体解决概率推理问题提供必要的元认知资源，从而导致较差的概率推理成绩．此外，从数学元认知的3个成分来看，数学元认知知识在数学焦虑与初中生概率推理关系中的中介作用不显著，而数学元认知体验、数学元认知监控的中介作用均显著．这验证了研究的假设H2．数学元认知的3个成分各有其功能．与数学元认知知识相比，数学元认知体验和数学元认知监控对概率推理的影响更大一些．数学元认知知识涉及个体知识、任务知识及策略知识，而数学元认知体验涉及成就感、焦虑感等数学学习过程中的情感体验，数学元认知监控涉及评价、检验及管理等[43]．随着认知任务难度的增大，学习者的认知体验、情感体验对解题过程中的方向、进展等调节和监控越加显著[36]．即使个体拥有数学元认知知识，但如果不会应用这些知识，再加上如果处于高数学焦虑水平，缺乏积极的数学元认知体验，难以进行有效的数学元认知监控，其概率推理水平也将不如人意．

有研究表明，当面对概率问题的时候，人们经常应用启发式，而不是用正式的分析程序和技术[44]．Stanovich（2011）[45]提出的三重加工心智模型（自主心智、算法心智以及反省心智）在双加工过程理论的基础上增加了“反省心智”，并强调了反省心智对自主心智产生的劣质反应的压制功能和发起产生优化反应的模拟仿真功能．研究中在对高概率推理水平的学生进行个别访谈时发现，在问题解决过程中，他们会不断地反省．以研究中所使用的概率推理量表第4题为例：“将一枚匀质硬币抛掷9次，则下列哪种情况最有可能发生？（H：正面，T：反面） A. THHTHTTHHB. HTHTHTHTH C. AB概率相同．”如果个体在面对这个问题的时候，犯了认知吝啬鬼的思维谬误，默认自主心智的加工，就会选择“B”，因为直觉告诉个体序列“B”比序列“A”更加随机．其实，正确答案是“C”．即选择了概率推理量表第4题正确答案的个体在解答题目的时候通过监控、调节、评价等，可以认为其发挥了反省心智的功能，压制了自主心智的劣质反应，再通过算法心智的功能发挥，最终做出了正确判断——A、B两个序列的概率是相等的．因此，可以从反省的角度，将元认知作为反省心智的一个衡量指标．

从性别的作用来看，研究发现，男生的数学焦虑水平先降后升，女生的数学焦虑水平先升后降．这可能是由于个体发育的性别差异所导致．与男生相比，女生更早进入青春逆反期，更容易出现焦虑．过了这个时期，焦虑等负面情绪体验会有所下降．男生和女生在概率推理水平、数学元认知水平的变化特点还和个体发育及后天学习有关．在数学表现方面，小学阶段之后，男生的优势增加，这种性别差异到中学、大学阶段就更加明显[46]．Primi等（2017）[12]研究发现，在概率推理上存在显著的性别差异，女性的概率推理表现显著低于男性．而该研究发现，男生和女生的概率推理表现无显著差异．这可能和选取的对象有关．前者以高中生和大学生为被试，而这里以初中生为被试．概率推理的性别差异问题有待于今后进一步探讨．有趣的是，研究发现，虽然男生的数学焦虑水平显著低于女生，数学元认知水平显著高于女生，但概率推理水平的性别差异不显著，而且，研究中部分验证了假设H3，即性别调节了数学焦虑经过数学元认知监控对概率推理的中介效应．与男生相比，女生数学元认知监控对概率推理的影响更强．也就是说女生能更好地调动数学元认知监控的功能，发挥数学元认知监控对概率推理的影响．元认知的核心思想是对自己认知过程的监视和控制[47]．意识的记忆监控模型显示，监控和自信有关[48]．一般来说，女性比男性更自信[49]．长期不同的经验塑造了不同的脑结构和机能[50]，再加上，与同年龄段的初中男生相比，女生发育更快一些，心智更成熟一些，更懂得如何在认知活动或问题解决中整合已有的认知资源．所以，尽管在数学学习中存在性别差异，但若重视元认知训练，增强学生的反省和监控能力，必定可以促进他们的数学学习．因此，教师面临的挑战不仅仅是为学生提供更多的概率学习体验，还要提供有意义的体验，从而促进他们对概念的正确理解[51]．在今后的数学教育和数学学习活动中，要尽可能地多给学生提供积极的、丰富的数学学习体验，通过元认知训练来促进学生概率推理能力的发展和数学素养的提高[52–59]．

综上，通过对431名初中生进行调查，阐明了数学焦虑对概率推理的影响、数学元认知的中介作用以及性别的调节作用，丰富了相关研究，并为数学教育工作者和学生家长提供了借鉴和参考．与此同时，研究中也存在一些局限．首先，这里主要采用问卷法，收集到的资料不够全面，未来的研究可以对初中生数学焦虑现状和概率推理水平发展现状开展焦点访谈和个案观察，深入探讨数学焦虑对概率推理的影响．其次，此研究为横向研究，未来的研究可以选取初一年级的学生，从他们入学开始，通过追踪研究深入剖析初中生数学焦虑水平和概率推理水平的发展变化．最后，研究发现数学元认知在中介数学焦虑对概率推理关系中的作用很大，缺乏进行进一步的干预研究和实践佐证，未来的研究可以通过开展数学元认知水平训练，操纵这一变量，从而在实践层面上验证数学元认知对概率推理的影响．

5 结论

（1）数学元认知在数学焦虑与初中生概率推理的关系中起中介作用．

（2）数学元认知知识在数学焦虑和初中概率推理的关系中不起中介作用，而数学元认知体验和数学元认知监控均起中介作用．

（3）性别调节了数学焦虑经过数学元认知监控对概率推理的中介效应．与男生相比，女生数学焦虑经过数学元认知监控对概率推理的中介效应显著增加．

[1] CHASSEIGNE G, MULET E, STEWART T R. Aging and multiple cue probability learning: The case of inverse relationships [J]. Acta Psychologica, 1997, 97 (3): 235–252.

[2] CHIESI F, PRIMI C, MORSANYI K. Developmental changes in probabilistic reasoning: The role of cognitive capacity, instructions, thinking styles, and relevant knowledge [J]. Thinking and Reasoning, 2011, 17 (3): 315–350.

[3] TVERSKY A, KAHNEMAN D. Judgment under uncertainty: Heuristics and biases [J]. Science, 1974, 185 (4 157): 1 124–1 131.

[4] STANOVICH K E, WEST R F. On the relative independence of thinking biases and cognitive ability [J]. Personality Processes and Individual Differences, 2008, 94 (4): 672–695.

[5] FISCHBEIN E, NELLO M S, MARINO M S. Factors affecting probabilistic judgments in children in adolescence [J]. Educational Studies in Mathematics, 1991, 22 (6): 523–549.

[6] STANOVICH K E. Metarepresentation and the great cognitive divide: A commentary on henriques’ “psychology defined” [J]. Journal of Clinical Psychology, 2004, 60 (12): 1 263–1 266.

[7] CHAPAMAN G B, LIU J. Numeracy, frequency, and Bayesian reasoning [J]. Judgment and Decision Making, 2009, 4 (1): 34–40.

[8] SIROTA M, JUANCHICH M, HAGMAYER Y. Ecological rationality or nested sets? Individual differences in cognitive processing predict Bayesian reasoning [J]. Psychonomic Bulletin & Review, 2014 (21): 198–204.

[9] 史滋福，邱江，张庆林．任务情境和证据信息对青少年贝叶斯推理的影响研究[J]．心理科学，2008，31（1）：181–184．

[10] ASHCRAFT M H. Cognitive psychology and simple arithmetic: A review and summary of new directions [J]. Mathematical Cognition, 1995, 1 (1): 3–34.

[11]  GANLEY C M, VASILYEVA M. The role of anxiety and working memory in gender differences in mathematics [J]. Journal of Educational Psychology, 2014, 106 (1): 105–120.

[12]  PRIMI C, MORANYNI K, DONATI M A, et al. Measuring probabilistic reasoning: The construction of a new scale applying item response theory [J]. Journal of Behavioral Decision Making, 2017, 30 (4): 933–950.

[13]  CAREY E, HILL F, DEVINE A, et al. The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance [J]. Frontiers in Psychology, 2016 (6): 1–6.

[14] 周双珠，韩瑽瑽，陈英和．数学焦虑影响数学学业成就的作用机制——数学元认知的中介作用[J]．数学教育学报，2014，23（5）：14–18．

[15] 张婕，黄碧娟，司继伟，等．乡镇小学生的数学焦虑与数学成绩：数学自我效能感和数学元认知的链式中介作用[J]．心理发展与教育，2018，34（4）：453–460．

[16] WOLTERS C A, PINTRICH P R. Contextual differences in student motivation and self-regulated learning in mathematics, English, and social studies classrooms [J]. Instructional Science, 1998, 26 (2): 27–47.

[17]  KAZUHIRO O, TETSUYA H. Beyond intelligence: A meta-analytic review of the relationship among metacognition, intelligence, and academic performance [J]. Metacognition and Learning, 2018 (13): 179–212.

[18] KLACZYNSKI P, COTTRELL J. A dual-process approach to cognitive development: The case of children’s understanding of sunk cost decisions [J]. Thinking and Reasoning, 2004 (10): 147–174.

[19]  KLACZYNSKI P A. Metacognition and cognitive two-process model of decision making and its development [M] // JACOBS J E, KLACZYNSKI P A. The development of decision making in children and adolescents. Mahwah, NJ: Lawrence Erlbaum, 2005: 39–76.

[20] 黄晓学．数学元认知在数学问题解决中的作用[J]．数学教育学报，1993，2（2）：88–89．

[21] 王光明，佘文娟，廖晶，等．高效率数学学习高中生的元认知特征及其教学意义[J]．教育科学研究，2017（4）：46–53，61．

[22] 崔克忍，王向华．元认知与数学思维[J]．教育理论与实践，2005（10）：55–57．

[23] 欧慧谋，唐剑岚．国内数学元认知的研究与思考[J]．课程·教材·教法，2012，32（5）：58–61．

[24] 范文贵，李伟华．西方数学学习性别差异研究述评[J]．比较教育研究，2008（9）：77–82．

[25]  ACKERMAN P L. Determinants of individual differences during skill acquisition: Cognitive abilities and information processing [J]. Journal of Experimental Psychology: General, 1988, 117 (3): 288–318.

[26]  HOFMANS J, MULLET E. Towards unveiling individual differences in different stages of information processing: A clustering-based approach [J]. Quality and Quantity, 2013, 47 (1): 455–464.

[27] BYRNE K A, WORTHY D A. Gender differences in reward sensitivity and information processing during decision-making [J]. Journal of Risk and Uncertainty, 2015, 50 (1): 55–71.

[28] 范叙保，汤炳兴，田中．数学能力成分的性别差异测试分析[J]．数学教育学报，1999，8（4）：70–73，81．

[29] AZEVEDO R, GUTHRIE J T, SEIBERT D. The role of self-regulated learning in fostering students’ conceptual understanding of complex systems with hypermedia [J]. Journal of Educational Computing Research, 2004 (30): 87–111.

[30] MEIJER J, VEENMAN M V J, VAN HOUT-WOLTERS B H A M. Metacognitive activities in text-studying and problem-solving: Development of a taxonomy [J]. Educational Research and Evaluation, 2006 (12): 209–237.

[31] 王芬芬，姜海燕．医学生的个人规划对学业成绩的影响：性别的调节作用[J]．教育与教学研究，2015，29（9）：49–51，56．

[32] JOHNSON M K, HIRST W. MEM: Memory subsystems as processes [M] // GATHERCOLE S, COLLINS A F, CONWAY M A, et al. Theories of memory. Brighton: Lawrence Erlbaum Associates, 1993: 241–286.

[33] 汤服成，何文林．中学生数学元认知知识的调查研究[J]．数学教育学报，2009，18（3）：39–41．

[34] WAVERING M J. Interrelationships among Piaget’s formal operational schemata: Proportions, probability, and correlation [J]. The Journal of Psychology, 1984, 118 (1): 57–64.

[35]  CHIESI F, PRIMI C, MORSANYI K. Developmental changes in probabilistic reasoning: The role of cognitive capacity, instructions, thinking styles, and relevant knowledge [J]. Thinking and Reasoning, 2011, 17 (3): 315–350.

[36] 吴明隆．国民中小学学生社会心理变因与数学焦虑及数学信念关系之研究[J]．教育学刊，1996（12）：287–327．

[37] 唐剑岚，周莹，汤服成．数学问题解决中的元认知问卷量表的设计[J]．数学教育学报，2005，14（4）：48–52．

[38] 方杰，温忠麟．基于结构方程模型的有调节的中介效应分析[J]．心理科学，2018，41（2）：453–458．

[39] VUKOVIC R K, KIEFFER M J, BAILEY S P, et al. Mathematics anxiety in young children: Concurrent and longitudinal associations with mathematical performance [J]. Contemporary Educational Psychology, 2013, 38 (1): 1–10.

[40]  EYSENCK M W, CALVO M G. Anxiety and performance: The processing efficiency theory [J]. Cognition and Emotion, 1992, 6 (6): 409–434.

[41]  WATSON J. The probabilistic reasoning of middle school students [M] // JONES G A. Exploring probability in school. New York: Springer, 2005: 145–169.

[42]  CAVIOLA S, CAREY E, MAMMARLLA I C, et al. Stress, time pressure, strategy selection and math anxiety in mathematics: A review of the literature [J]. Frontiers in Psychology, 2017 (8): 1–13.

[43] 崔宝蕊，李健，王光明．初中生数学元认知水平调查问卷的设计与编制[J]．数学教育学报，2018，27（3）：45–51．

[44]  TVERSKY A, KAHNEMAN D. Judgment under uncertainty: Heuristics and biases [J]. Science, 1974, 185 (4 157): 17–34.

[45]  STANOVICH K E, WEST R F, TOPLAK M E. The complexity of developmental predictions from dual process models [J]. Developmental Review, 2011 (31): 103–118.

[46] 徐速．小学数学学习心理学研究[M]．杭州：浙江大学出版社，2006：214．

[47] 张庆林．元认知的发展与主体教育[M]．重庆：西南师范大学出版社，1997：10．

[48]  NELSON T O, NARENS L. Metamemory: A theoretical framework and new findings [J]. Psychology of Learning and Motivation, 1990 (26): 125–173.

[49]  PALLIER G. Gender differences in the self-assessment of accuracy on cognitive tasks [J]. Sex Roles, 2003 (48): 265–276.

[50]  BYRNES J P, HONG L, XING S. Gender differences on the math subtest of the scholastic aptitude test may be culture-specific [J]. Educational Studies in Mathematics, 1997, 34 (1): 49–66.

[51]  HOURIGAN M, LEAVY A. What do the stats tell us? Engaging elementary children in probabilistic reasoning based on data analysis [J]. Teaching Statistics, 2015, 38 (1): 8–15.

[52] 王光明，李爽．初中生数学学习非智力因素调查问卷的编制[J]．数学教育学报，2020，29（1）：29-39．

[53] 傅海伦，张丽，王彩芬．基于Fuzzy-AHP质疑式数学核心素养评价指标体系的研究[J]．数学教育学报，2020，29（1）：52-57．

[54] 孙思雨，朱雁．初中生数学自我效能感及其校准性的调查研究[J]．数学教育学报，2019，28（6）：27-32．

[55] 陈蓓．知识图谱可视化分析下的数学核心素养研究[J]．数学教育学报，2019，28（6）：87-91．

[56] 郑毓信．“数学深度教学”的理论与实践[J]．数学教育学报，2019，28（5）：24-32．

[57] 朱先东．指向深度学习的数学整体性教学设计[J]．数学教育学报，2019，28（5）：33-36．

[58] 程靖，鲍建生．“四基”：中国特色数学教育体系的核心理念[J]．数学教育学报，2019，28（3）：2-6．

[59] 宁锐，李昌勇，罗宗绪．数学学科核心素养的结构及其教学意义[J]．数学教育学报，2019，28（2）：24-29．

Students’ Mathematics Anxiety and Their Probabilistic Reasoning in Middle School: A Metacognition Related Mediation Model

SHI Zi-fu, XIE Yun-tian

(Department of Psychology, Hunan Normal University, Cognition and Human Behavior Key Laboratory of Hunan Province, Hunan Changsha 410081, China)

This study investigated 431 middle school students’ mathematics anxiety and its relationship to these students’ probabilistic reasoning using Mathematical Anxiety Scale, Probabilistic Reasoning Scale, and Mathematical Metacognition Scale. The results show that: (1) Mathematical metacognition plays a mediating role in mathematical anxiety and probabilistic reasoning; (2) metacognitive knowledge in mathematics has no significant mediating role between mathematical anxiety and probabilistic reasoning; (3) metacognitive experience and metacognitive monitoring in mathematics have significant mediating roles between mathematical anxiety and probabilistic reasoning; and (4) There is a gender moderated the mediating effect of mathematical anxiety on probabilistic reasoning through metacognitive monitoring in mathematics. Compared to male students, the mediating effect of female students’ mathematical anxiety on probabilistic reasoning under metacognitive monitoring in mathematics was significantly increased. Therefore, there is a moderating mediating effect between mathematics anxiety and probabilistic reasoning in middle school.

probabilistic reasoning; mathematical anxiety; mathematical metacognition; gender

G632

A

1004–9894（2020）04–0013–07

史滋福，谢云天．数学焦虑对初中生概率推理的影响——一个有调节的中介模型[J]．数学教育学报，2020，29（4）：13-19．

2020–03–09

湖南省教育厅科学研究重点项目——基于“三重加工心智模型”的青少年概率推理的认知机制研究（16A143）；湖南省研究生科研创新项目——青少年元认知潜在类别与数学学业成绩关系的追踪——基于潜变量混合增长模型的研究（CX20190343）

史滋福（1969—），女，山西太谷人，教授，博士生导师，主要从事思维心理学、数学心理学和心理统计学研究．

[责任编校：周学智、张楠]