基于创课导学的把课堂还给学生的数学教学实践

张享发　戴陈敏

【摘 要】本文阐明创课导学的课堂教学方法的内涵，以“直线与双曲线位置关系”为例，阐述创课导学的课堂教学方法的具体应用，创设让学生“再创造”的数学课堂，通过问题导向、实验导学，把课堂的时间、空间、个性还给学生。

【关键词】数学课堂 创课导学 再创造 问题导向 实验导学

【中图分类号】G  【文献标识码】A

【文章编号】0450-9889（2020）04B-0109-03

荷兰著名数学教育家弗赖登塔尔（1905—1990）认为：“数学教学方法的核心是学生的‘再创造。”他认为在数学教学中，教师应该提供适合作为知识载体的具体情境，使学生通过实践探究，自己“再创造”出概念、法则、定理、公理等数学知识。《普通高中数学课程标准（2017 年）》指出，现代信息技术要“致力于改变学生的学习方式，使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去”。因此，在高中数学课堂教学中，如何创设适合学生“再创造”的教学环境，把课堂还给学生，让学生真正成为课堂的主人，是摆在数学教师面前的新课题。

创课导学是基于广西师范大学唐剑岚博士数学实验创课的观点开展的课堂教学方法。依据高中数学创课导学的课堂教学方法，在日常的高中数学课堂教学中，借助信息技术、实物教具等实验工具可以创设一个让学生“再创造”的数学实验环境，通过关键问题的导向，让学生在动手“实验”的过程中经历观察、猜想、推理等科学方法，主动建构数学模型，养成“用数学”的习惯，从而提升数学素养。现以具体的教学案例对此进行阐述。

一、研究的主要问题

〖问题 1〗过点（0，1）可以作几条直线与双曲线 4x2-y2=4 有且只有一个公共点？

〖问题 2〗过点（0，1）的直线与双曲线 4x2-y2=4 的交点有几种情况？

〖问题 3〗若直线 l 过定点（，0），双曲线：x2-2y2=2。（1）若直线 l 与双曲线有且仅有一个公共点，求直线 l 的方程;（2）若直线 l 分别与双曲线的两支各有一个公共点，求直线 l 斜率的取值范围。

二、重难点突破办法

将教室虚拟为实验室，借助图形计算器、iPad、希沃电子白板等工具构建实验平台，让学生围绕课堂核心问题，创设实验。猜想交点的图形特征，积累分析交点特征的实验猜想经验。通过实验平台动手操作、合作探究、感悟思想、建构知识。

三、教学模式

创课导学的基本模式是：问题—实验—解惑。

四、教学过程

〖问题 1〗

[师]前面我们用什么方法判定直线与椭圆的位置关系？

[生]首先，几何方法，通过图象观察交点个数;其次，代数方法，联立方程组分析根的个数。

[师]如何用几何方法判断过点（0，1）可以作几条直线与双曲线 4x2-y2=4 有且只有一个公共点？

〔学生活动〕大家都尝试在纸上画出过已知点的直线以及相应的双曲线的示意图。由于多数同学所画的双曲线没有突出双曲线有两条渐近线的图形特征，因此通过示意图很难直观判断交点情况。教师随堂巡视，进行个别指导。

学生先在纸上徒手画图，发现无法准确判断交点情况后，再借助图形计算器或 iPad 进行探究求证。通过直线斜率的变化观察直线与双曲线的交点个数情况，找出符合条件的直线。充分交流后形成如下结论：

1.过点（0，1）的直线主要由斜率 k 决定。

2.当直线斜率 k 与双曲线的渐近线不平行时，分别与左支、右支曲线各有 1 条直线满足条件（通过图形计算器、iPad，改变直线的斜率，观察验证）。

3.当直线斜率 k 与双曲线的渐近线平行时，分别与左支、右支曲线各有 1 条直线满足条件（通过图形计算器、iPad，改变直线的斜率，观察验证）。

4.示意图如图 1 所示。

[师]利用代数方法求解时，能否分别求出这四条直线的斜率？

〔学生活动〕尝试联立直线与双曲线的方程组进行求解，利用二次项系数等于零以及判别式等于零，分别求出对应斜率的个数，最后相互验证几何方法、代数方法所得出的结论。

归纳总结：（1）过定点的直线，主要由斜率来确定位置，通过斜率的变化能形成直线束;（2）判断交点个数，先要明确直线斜率与双曲线渐近线的位置关系;（3）联立方程组既可以判断交点个数，又可以明确交点的坐标。

〖问题 2〗

[师]通过刚才的实验，直线与双曲线有哪几种交点的情况？

[生]有三种情况，无交点，1 个交点，2 个交点。

[师]这三种情况下交点的分布有哪几类？

[生]没有交点，左支一个，右支一个，左支两个，右支两个，左右各一个。

实验探究：过点（0，1）的直线与双曲线 4x2-y2=4 的交点有几种情况？请利用图形计算器或 iPad 进行分析总结：随着直线斜率的变化，直线與双曲线的交点的变化情况。记录并填入下表，并用图形计算器演示对应的各种图象。

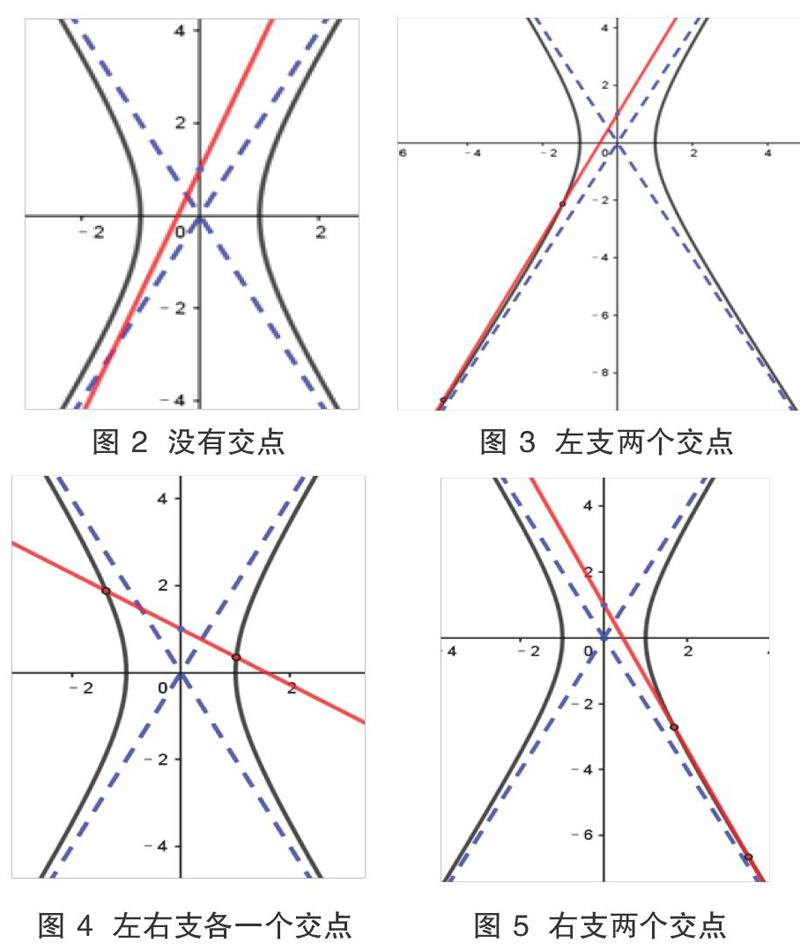
〔学生活动〕利用图形计算器或 iPad，通过改变直线的斜率，观察交点的变化，并进行记录。除了以上的只有一个交点的情况外，有两个交点的情形分别是图 3，图 4，图 5，没有交点的情况如图 2。

按照斜率从小到大的次序归纳 k 的取值范围与交点个数的情况，如下：

过定点（，0）的直线 l 与双曲线 x2-2y2=2 的各种交点的情况，可通过旋转直线 l 来实现（如图 6 所示）。

归纳总结：根据图形计算器图象中交点的变化情况，可以发现交点个数按逆时针旋转的变化，其规律为：没有交点——右支 1 个—— 右支 2 个—— 右支 1 个—— 左右各 1 个—— 左支 1 个—— 左支 2 个—— 左支 1 个—— 没有交点。旋转的时候，主要是直线斜率在变化。

〖问题 3〗

學生利用之前的探究成果独立解题，然后小组交流，检验学习成效。

[第（1）问]

方法一：几何法。通过双曲线方程可以得出定点（，0）正好是双曲线的右顶点，通过作图（如图 7 所示）可以看出，直线与双曲线相切或者与渐近线平行时都是只有一个交点，容易确定直线方程。

方法二：代数法。当直线斜率不存在时，直线 l 为  符合题意;当直线斜率存在时，设直线方程为 ，联立直线与双曲线的方程组，利用判别式等于零，即可求出直线的方程。

[第（2）问]同学们巩固解题方法，加深对两种方法的理解与认识。

归纳总结：通过对比发现，几何法讲究数形结合，通过作图，观察图形变化的特点，能快速解决交点问题。代数方法则通过联立方程组，通过二次项系数为零或者二次方程的根来确定方程组的根，进而确定交点的坐标及交点个数，两种方法，各有优劣。

五、教后总结

本案例是基于高中数学创课导学的课堂教学实践，较为成功地展示创课导学“问题导向，实验导学”的课堂教学理念。本案例依托现代信息技术，借助图形计算器、iPad、希沃电子白板等工具构建实验平台，围绕课堂核心问题，创设让学生“再创造”的数学课堂，通过开展实验探究，把数学课堂还给学生。主要体现在以下三个方面：

（一）把课堂的时间还给学生。高中数学创课导学以帮助学生解惑、提升学生数学素养为根本任务。在本案例中，“创课”从设置系列背景问题开始，借助实验工具，通过实验、演示、推导，不断让学生动手实践。学生在实践过程中动脑、动心、动情、动手，并在探究过程中掌握类比、观察、猜想等学习方法。在导学过程中，始终将学生置于研究者、探索者的位置。学习探索需要过程，有过程就需要时间。在学生进行主动探索、合作探究中，我们既要确保学生学习的时间，又要把学习的主动权还给学生，从而使学生的数学知识得到增加，数学能力得到提高。

（二）把课堂的空间还给学生。高中数学创课导学以“问题导向，实验导学”为设计理念，重视科学思想和数学方法的引导。在本案例的课堂教学过程中，让学生经历遇到实际问题、创设情境、实验探究、小组合作、归纳结论等过程，使学生灵活运用观察、分析、归纳等科学方法。学生围绕“问题”“实验”探究的过程是一个主动参与课堂学习的过程，有实践、有交流、有质疑、有展示、有体验，在规律形成的总结中发展了学生的思维空间，在实验成果的汇报中锻炼了学生的表现空间。

（三）把课堂的个性还给学生。高中数学创课导学注重培养学生的个性化思维。创课导学的课堂教学过程提倡的是充分调动学生的学习积极性，发挥学生的自主能动性。在本案例的教学中，围绕核心问题，开展实验探究。学生动手操作，并经历独立思考、独特感悟、自由联想、自由表达的过程。实验探究的过程，既是交流合作的过程，又是知识生成的过程。在这个过程中，会有问题分析的异中求同，也会有问题解决的成功体验，学生的个性化思维得到发展，使学生在实验中感悟思想，在体验中建构知识。

【参考文献】

[l]唐剑岚，黄一娉，黄梦远.基于5E学习环和HP工具的数学实验创课设计：以《函数图象变换》的教学为例[J].数学周报，2016（9）.

[2]弗赖登塔尔.作为教育任务的数学[M].上海：上海教育出版社，1995.

（责编 卢建龙）