智能网联车环境下考虑反应时间影响的基本图模型

徐桃让,姚志洪,3,蒋阳升,杨 涛

(1. 西南交通大学 交通运输与物流学院, 四川 成都 611756； 2. 综合交通大数据应用技术国家工程实验室, 四川 成都 611756； 3. 重庆交通大学 重庆市交通运输工程重点实验室,重庆 400074； 4. 中铁第一勘察设计院集团有限公司,陕西 西安 710043)

0 引言

随着国家政策对智能网联车发展的推动，智能网联车技术正在日益发展和完善。最新研究[1]表明至2050年道路上的智能网联车比例将达到约75%左右，因此未来较长的时间内道路上的交通流将表现为由传统人工驾驶车辆(即人工车)和智能网联车组成的异质流。由于这种异质交通流的诸多特性与原单一人工车流不同，因此研究这种异质交通流特性对提高交通流运行效率具有显著的理论意义和实用价值。

国外学者对异质交通流特性的研究已取得较为丰富的成果，涉及通行能力[2-3]、交通流稳定性[4-5]等方面。Kesting等[2]通过改变智能驾驶员模型中的相关参数分别模拟人工车跟驰模型和智能网联车跟驰模型，并通过对匝道仿真表明在智能网联车的比例达到25%时匝道的通行能力能得到明显提高。Shladover等[3]考虑了智能网联车在跟驰人工车时的功能退化，仿真研究了高速公路路段的通行能力。在稳定性的研究方面，Lu等[4]研究了由智能网联车组成的交通流的稳定性条件，并通过数值模拟验证了所提出准则的正确性，但缺乏对人工车影响智能网联车条件下异质交通流稳定性的研究。Talebpour等[5]建立了不同智能网联车比例的异质交通流稳定性分析框架，结果表明增大智能网联车比例不仅能提高交通流通行能力，也能有效防止冲击波的产生和传播。

国内学者对异质交通流的研究也已取得一些成果，涉及异质交通流的交通安全[6-7]、稳定性分析[7-10]、基本图模型[9-11]以及通行能力[9-11]等方面。Xie等[8]推导出考虑反应时间的异质交通流线性稳定性条件，通过代入智能驾驶员模型表明智能网联车比例的增加能够提高交通流的稳定性和效率。秦严严等[9,11]用智能驾驶员模型模拟人工车的跟驰行为，使用PATH实验室标定的智能网联车模型模拟智能网联车的跟驰行为，研究了混合交通流的稳定性，并以期望车间时距作为退化后智能网联车与未退化智能网联车的区别项推导了包含智能网联车比例的基本图模型。Yao[10]等分别采用全速度差模型与CACC模型模拟人工车与智能网联车的驾驶行为，并通过求异质交通流的平均车头间距推导出了异质交通流的基本图模型。

通过以上分析可以发现，国内外学者对混有智能网联车的异质交通流研究涉及多个方面，但对其基本图的研究并未考虑反应时间的影响。具体表现在以下两个方面：一方面，鲜有文献在研究异质交通流的基本图模型时考虑了不同类型车辆反应时间的差异，并以此来修正跟驰模型。而智能网联车对交通流的影响本质上源于期望车头间距、反应时间等性能与常规车存在的差异，故反应时间对异质交通流的特性有重要的影响。另一方面，考虑反应时间的研究[12-15]目前主要集中于同质交通流，在人工车与智能网联车组成的异质交通流中极少。因此，本研究采取智能驾驶员模型来同时模拟异质交通流中不同类型车辆的跟驰行为，并在此基础上考虑不同跟驰模式的反应时间，以反应时间的差异区分两种不同类型的车辆，推导出了异质交通流基本图模型，对比分析了考虑反应时间后IDM的合理性与优势，并对模型中交通流通行能力的影响因素进行了敏感性分析，最后通过数值仿真试验验证了模型的正确性与有效性。

1 跟驰模式分析

对于同时存在智能网联车和人工车的混合交通流车队，通过组合分析可知，共存在如图1中所示的4种跟驰模式[8]。

(1) 人工车跟驰人工车

若本车为人工车，前车也为人工车，此时如果前车突然改变驾驶行为(如加减速等)，本车驾驶员首先需要对前车驾驶行为的变化进行感知、识别、判断，再做出决策。该过程需要一定的时间，本研究称为反应时间。这种跟驰模式如图1 (a)所示。

(2) 人工车跟驰智能网联车

若本车为人工车，前车为智能网联车，与第(1)种情况一样，本车也需要对前车行为的变化进行感知、识别、判断再做出决策。因此，其反应时间与模式(1)相同。这种跟驰模式如图1(b)所示。

(3)智能网联车跟驰人工车

若本车为智能网联车，前车为人工车。这种情况下，当前车驾驶行为变化时(如加减速等)，本车通过各种传感设施设备能够迅速、精确地判断出前车的驾驶行为并立刻做出应对措施。因此其反应时间较模式(1)和式(2)更短，但由于前车为人工车，尚不能形成车车通讯。这种跟驰模式如图1(c)所示。

(4) 智能网联车跟驰智能网联车

若本车为智能网联车，前车也为智能网联车。该情况下前车的驾驶行为变化信息可直接通过车车通讯传递给本车，前后车基本可以实现同步改变驾驶行为。因此，该情况下的反应时间可看作车车之间的通讯延误和控制延误，可认为这两辆车以车队形式行驶，即反应时间为0。这种跟驰模式如图1 (d)所示。

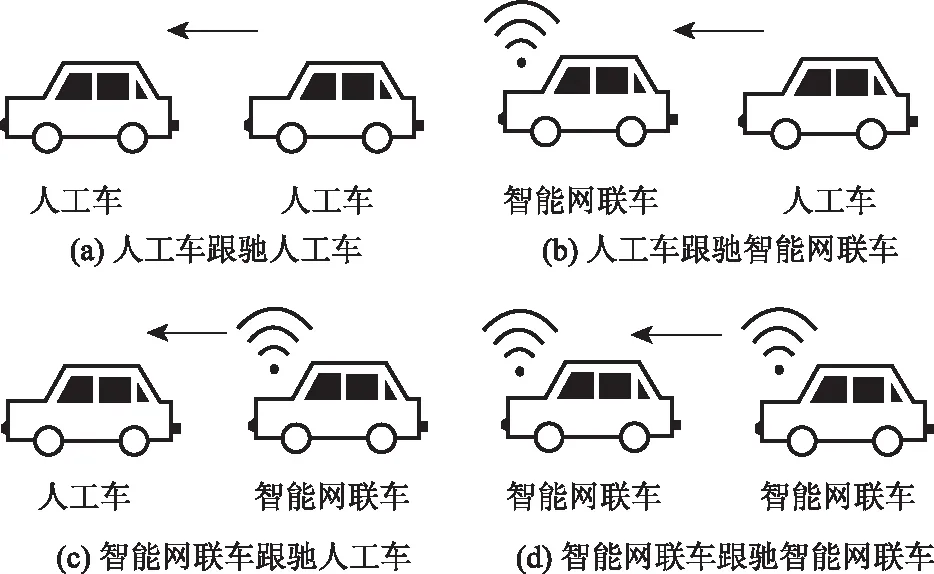
图1 异质交通流中的跟驰模式Fig.1 Car-following modes in heterogeneous traffic flow

1.1 车辆比例关系

假设道路上异质交通流车队中智能网联车所占的比例为P，则从概率论的角度出发可得上述4种跟驰模式的比例，如表1所示[8]。

表1 跟驰模式比例Tab.1 Proportion of car-following modes

1.2 比例关系验证

参考已有研究[11]，对于表1中提出的各种跟驰模式的比例关系结合解析阐述和随机性仿真试验进行验证。

1.2.1解析阐述

由于道路上的车辆数量是守恒的，故表1中推导出的各种跟驰模式的比例在理论上应满足式(1)：

(1)

式中，3个约束条件的含义分别为：跟驰人工车的人工车(比例为Prr)和跟驰智能网联车的人工车(比例为Prc)二者比例之和应等于总的人工车的比例(比例为Pr)；跟驰人工车的智能网联车(比例为Pcr)和跟驰智能网联车的智能网联车(比例为Pcc)二者比例之和应等于总的智能网联车比例(比例为Pc)；人工车比例与智能网联车比例之和应等于1。

将表1中各种跟驰模式的表达式代入式(1)中进行验算，发现表1中的关系表达式均满足式(1)中约束的要求。

1.2.2随机性仿真验证

为了进一步验证表1中各种跟驰模式比例的正确性，借助MATLAB软件设计随机性仿真试验，验证流程如图2所示。

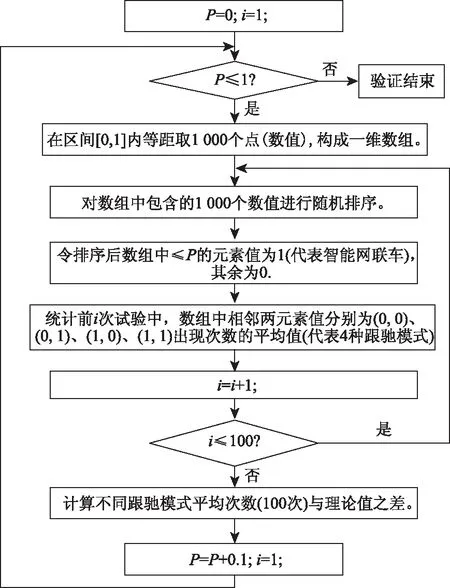
图2 比例验证流程Fig.2 Flowchart of proportion validation

图2中P值为智能网联车比例，i为每一P值下随机性试验的次数。将P值从0至1按步长为0.1进行取值，得到每一P值下100次随机性仿真试验中各种跟驰模式数量的平均值与表1对应关系式计算值之间的差值，如图3所示。

图3 比例验证结果Fig.3 Result of proportion validation

图3中人工车跟驰模式指人工车跟驰人工车和人工车跟驰智能网联车两种跟驰模式。由图3可知人工车跟驰模式数量的误差在2 veh(0.2%)以内，智能网联车跟驰人工车模式的数量误差在7 veh(0.7%)以内，智能网联车跟驰智能网联车模式的数量误差在8 veh(0.8%)以内，因此能够证明表1中推导出的各种跟驰模式比例有效可用。

2 跟驰模型

2.1 智能驾驶员模型

已有研究中，人工车辆跟驰行为的跟驰模型有智能驾驶员模型[16-18](Intelligent Driver Model, IDM) 以及全速度差模型[19-20]等，其中较多研究采用智能驾驶员模型。智能网联车跟驰模型有PATH实验室标定的CACC模型[21-22]，同时也有部分研究[15-16]采用IDM模型。IDM模型由德国学者Treiber等[16]提出，该模型参数的物理意义清晰明确，应用范围较广。因此，采用智能驾驶模型来描述人工驾驶车和智能网联车的跟驰行为。模型表达式如式(2)所示。

(2)

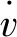
2.2 反应时间

如引言所述，相关研究[9,11]采用IDM模型研究车辆之间的跟驰行为时没有考虑反应时间。实际驾驶过程中驾驶员做出相关操作需要一定的反应时间。在IDM模型表达式中的最小停车间距s0为常数值，没有考虑不同车辆类型(智能网联车和人工驾驶车辆)反应时间的差异。

故考虑反应时间τ内车辆前进的距离，将式(2)中s0替换为s，如式(3)所示。

s=s0+vτ,

(3)

式中τ为反应时间。

故考虑反应时间后的IDM模型形式为：

(4)

式中各符号意义同前。

2.3参数设置2.3.1人工车跟驰模式

当人工车跟驰人工车或智能网联车时，两种跟驰模式的反应时间相同，故统称其为人工车跟驰模式。设人工车驾驶员的反应时间为τ1，则人工车跟驰模式下的最小安全间距可表示为：

s=s0+vτ1。

(5)

2.3.2智能网联车跟驰模式

(1) 智能网联车跟驰人工车：设智能网联车识别前车驾驶行为变化所需要的时间为τ2，则该跟驰模式下的最小安全间距可表示为：

s=s0+vτ2。

(6)

(2) 智能网联车跟驰智能网联车：设智能网联车之间的通信和控制延误(反应时间)为τ3，则此跟驰模式下的最小安全间距可表示为：

s=s0+vτ3。

(7)

2.3.3参数取值

参考相关文献[8]研究车流稳定性时对不同车辆反应时间的取值，取人工车驾驶员的反应时间τ1为0.4 s；智能网联车之间的通信延误很小，取τ3为0；智能网联车跟驰人工车模式下由于无法实现车车通讯，故识别反应时间介于前述二者之间，取τ2为0.2 s；IDM模型中其他参数的取值参考文献[11]，如表2所示。

表2 IDM模型不同参数取值Tab.2 Values of different parameters in IDM

3 异质交通流基本图模型

3.1 基本图模型

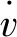
(8)

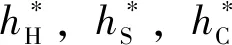
由表1可知：

人工车跟驰模式比例为Pr=(1-P)(1-P)+(1-P)P=1-P；智能网联车跟驰人工车的比例为：Pcr=P(1-P)；智能网联车跟驰智能网联车的比例为：Pcc=P2。

参考已有研究[9-11]，在混合交通流车队中，可将各种跟驰模式稳定状态下车头间距的平均值作为车队的车头间距。设混合交通流车队稳定状态下的总车辆数为N，则其车头间距可以表示为式(9)：

(9)

式中H*为混合交通流稳定状态下的车头间距。

根据交通流密度与车头间距之间的关系，可得密度的表达式如式(10)所示:

(10)

式中k为混合交通流的密度。

将公式(8)、(9)代入式(10)，得到密度与速度的关系式，如式(11)所示：

(11)

同理，根据流量、密度和速度之间的宏观交通流关系式，可进一步得到流量和速度之间的关系式，如式(12)所示：

(12)

式中，Q为流量。

基于以上分析，根据式(11)和式(12)可绘制不同智能网联车比例P下混合交通流流量、密度和速度之间的关系图，如图4所示。

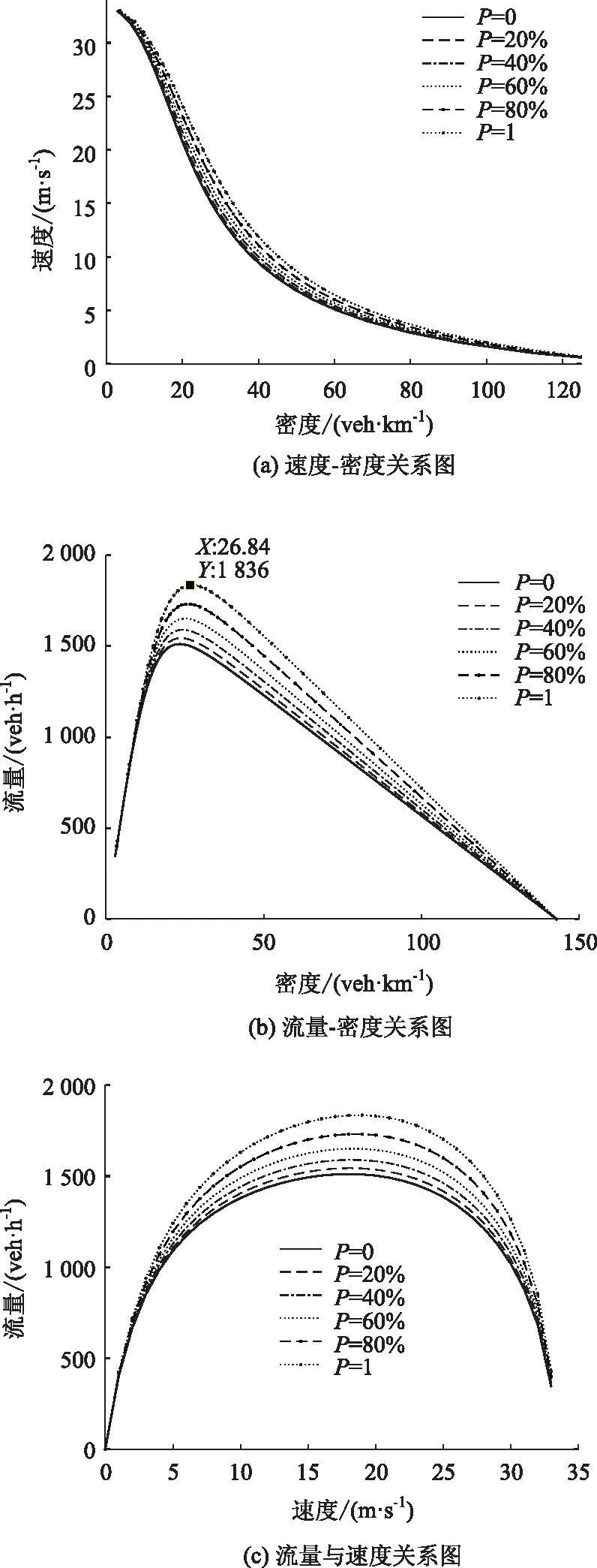
图4 不同智能网联车比例下异质交通流流量、密度和 速度关系Fig.4 Relationship among volume, density and velocity of heterogeneous traffic flow under different proportions of intelligent connected vehicles

由图4可知，在相同的密度和速度下，随着智能网联车比例的增加，道路的通行能力增加，说明异质交通流通行能力与智能网联车比例正相关。进一步可从图4 (b)中发现，当智能网联车比例为100%时，对应交通流的最佳密度为26.84 veh/km，此时的通行能力为1 836 veh/h。分析可知，当不考虑车辆的反应时间时，人工车与智能网联车在IDM模型中各项参数取值均相同，此时异质交通流可以视为同质流，异质交通流基本图模型的表达式将与智能网联车的比例无关，其流量-密度-速度关系图不受P值影响且与图4中P=1时的曲线完全相同(P=1时基本图模型表达式中反应时间项的值为0)，这与实际情况不符。考虑反应时间后，由于不同类型车辆的反应时间不同，异质交通流基本图模型表达式便会包括反应时间项，此时便与车辆组成有关，且由图4结果可知考虑反应时间后随着智能网联车比例的增大，异质交通流的通行能力增大，这说明反应时间对异质交通流的性质具有显著的消极影响作用(P值越大，车流整体的反应时间越小)，也说明考虑反应时间后的IDM模型与实际更相符。混合交通流的通行能力不会无限增大，结合式(12)分析原因可知与IDM模型中的其他参数如自由流速度、最小安全车距等有关。故以下基于流量-密度关系图分析混合交通流通行能力对各项参数的敏感性。

3.2敏感性分析3.2.1自由流速度

在IDM模型中的其他参数取值保持不变的情况下，仅改变自由流速度vf的取值，分析不同自由流速度下混合交通流的基本图。当自由流速度vf依次取15，20，25，30 m/s时，对应的流量-密度关系图如图5所示。

由图5可知，随着自由流速度的增大，混合交通流的通行能力逐渐增大。当自由流速度为15，20，25和30 m/s时，混合交通流的最佳密度分别为41.71，37.83，31.99和29.38 veh/km，对应的流量为1 501，1 634，1 727和1 798 veh/h。

3.2.2最小安全车距

在IDM模型中的其他参数取值保持不变的情况下，仅改变最小安全车头间距s0的取值，分析不同最小安全车头间距下混合交通流的基本图。当最小安全车头间距s0依次取1.4，1.6，1.8，2.0 m时，对应的流量-密度关系图如图6所示。

由图6可知随着最小车头间距的增加，混合交通流的最大通行能力递减。当最小车头间距分别为1.4，1.6，1.8，2.0 m时，混合交通流的最佳密度为27.31，27.15，26.99，26.84 veh/km,对应的最大流量为1 868，1 857，1 846，1 836 veh/h。进一步可以发现，最小车头间距每增加0.2 m，混合交通流的最佳密度减小量约为0.15 veh/km，对应最大流量减小量约为10 veh/h。故与前自由流速度相反，减小最小车头间距有利于增大混合交通流通行能力。

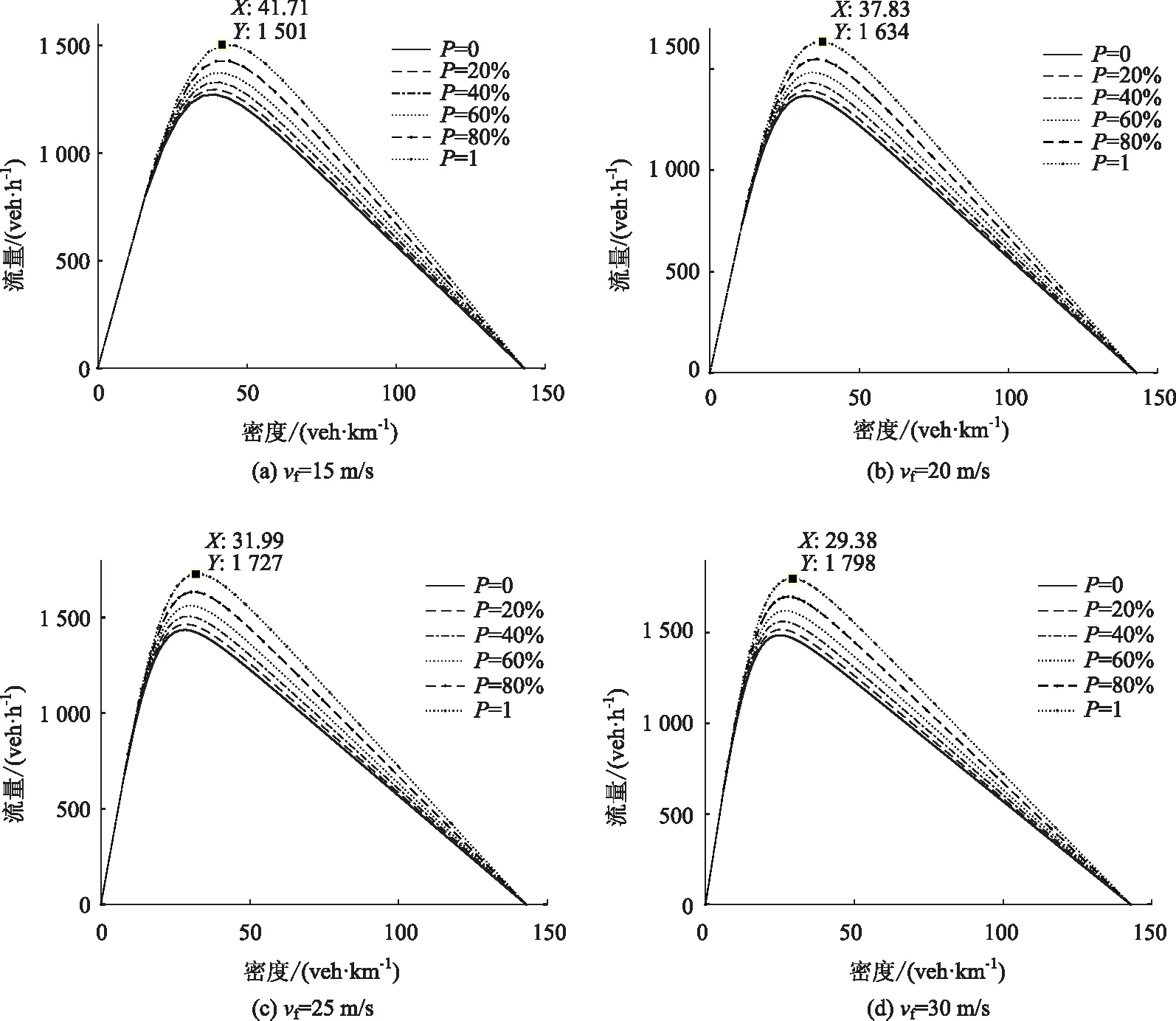
图5 自由流速度对异质交通流通行能力的影响Fig.5 Influence of free flow velocity on capacity of heterogeneous traffic flow

图6 最小车头间距对异质交通流通行能力的影响Fig.6 Influence of minimum headway on capacity of heterogeneous traffic flow

4 数值仿真

4.1 仿真环境设置

为验证本研究混合交通流基本图解析模型的正确性与有效性，设计仿真试验。参考相关文献[9-11]，其中仿真路段设置如图7所示，不考虑车辆变道行为。该路段为包含主干道上游、过渡区、限速区和匝道汇入区的单车道路段，每个区域内均有对应的长度和最高限速值。在匝道区采用随机减速的机制模拟匝道汇入车辆对主路车辆的影响。主干道上游车辆以自由流速度120 km/h驶入路段，在驶入距离超过3 km后进入减速过渡区段，最高限速为100 km/h，行驶距离超过5 km后进入长度为2 km、最高限速为80 km/h的限速区，然后进入长度为2 km、限速为60 km/h的匝道区，经过匝道区后车辆最高限速值逐步增加。在仿真时采用速度与行驶距离函数来控制车辆在不同路段处的最高限速值。在过渡区、限速区和匝道区铺设虚拟检测器，检测器间隔为500 m，每隔5 min统计检测区域内的交通流量和密度用以绘制流量-密度散点图。车辆组成由P值决定，不同类型车辆的到达随机且服从泊松分布。为了统计不同P值下路段的最大流量，将路段的车辆输入设为3 000 veh/h，远大于单车道通行能力(美国交通研究委员会研究成果表明，在标准小汽车的情况下，一条车道的基本通行能力为2 000 veh/h)。仿真时长为3 600 s，仿真精度为1秒/仿真秒，同一智能网联车比例下使用不同的随机种子仿真3次[9-11]。

图7 仿真路段示意图Fig.7 Schematic diagram of road section in simulation

4.2 仿真结果分析

仿真试验中不同跟驰模式的反应时间及IDM模型中其他各项参数的取值同前参数设置部分。仿真获得不同智能网联车比例条件下宏观交通流流量-密度关系图，其中智能网联车辆的比例P取值分别为0，20%，40%，60%，80%和100%。仿真结果如图8所示，其中曲线为理论曲线，黑色点为仿真采集的密度-流量数据。

由图8可知：(1) 不同智能网联车比例条件下，仿真数据波动性较大，部分仿真数据与理论曲线有较大差异，主要原因为仿真环境下交通流很难达到稳定状态，导致部分非稳定状态下的数据与理论值差值较大；(2) 仿真数据虽然有所波动，但均在理论曲线两侧，整体趋势与理论结果一致，证明了本研究混合交通流基本图解析结果的有效性；(3) 随着智能网联车比例的增加，散点图对应的最大流量也逐渐增大，流量-密度散点整体向上提升，与解析模型分布曲线的趋势一致，证明了解析模型的正确性。

5 结论

考虑了智能网联车环境下不同跟驰模式的反应时间，基于智能驾驶员模型，推导出了混合交通流的基本图模型，并通过参数敏感性和数值仿真试验得出以下结论：

(1) 随着智能网联车辆比例的增加，路段的通行能力逐渐增大，说明提高智能网联车辆比例能够有效提高现有道路的通行能力，也说明反应时间对异质交通流的通行能力具有显著的消极影响作用。

(2) 自由流速度越大，对应的混合交通流通行能力也越大；最小安全间距越大，道路通行能力越小，且最小车头间距每增加0.2 m，混合交通流的最佳密度减小约为0.15 veh/km，对应最大流量减小约为10 veh/h。

(3) 仿真结果与解析结果基本一致，证明了本研究宏观交通流基本图解析模型的正确性和有效性。

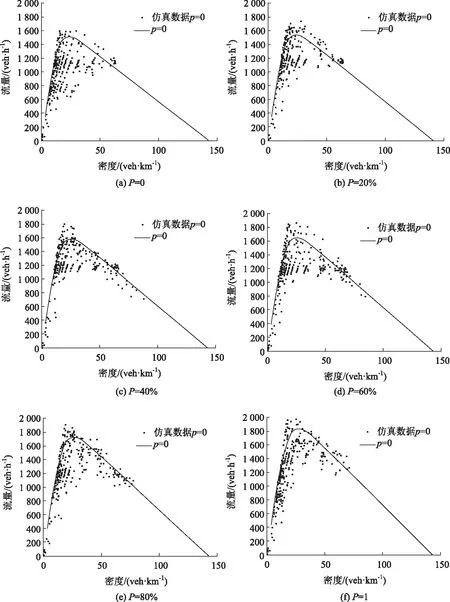
图8 仿真结果Fig.8 Simulation result

文章的创新点在于考虑了车联网环境下不同跟驰模式反应时间的差异，将其反映在了跟驰模型中，并以改进后的跟驰模型为基础推导出了基本图模型。在研究不同跟驰模式时，本研究均采用了智能驾驶员模型，因此进一步研究可通过考虑采用不同的跟驰模型来分别模拟不同类型的跟驰模式。同时，文章在对模型进行数值仿真验证时采用了含有上匝道与限速区的单车道，未考虑实际交通环境中换道行为对车辆跟驰行为的干扰，故未来可进一步考虑在双车道或更加复杂的交通环境下进行仿真验证，从而提高仿真的准确性。