高陡坡土工格栅加筋土堤地震动力响应分析

段彦福，刘 杰，宋 亮，麻 佳

(1. 新疆交通规划勘察设计研究院，新疆 乌鲁木齐 830006；2.石河子大学，新疆 石河子 832003)

0 引言

土工格栅加筋陡坡土堤具有良好的抗震性能，然而这种结构的抗震设计理论研究还不完善，动力响应尚不明确，阻碍了这一结构形式在工程中的大量应用。近几年国内外学者在土工格栅加筋结构领域研究较多，吴燕开等[1]、蒋建清等[2]、汪益敏等[3]，进行了数值模拟方面的研究。胡幼常等[4]、李亮[5]等，进行了理论方面的研究。李庆海等[6]、王丽艳等[7]、朱宏伟等[8]、El-Emam M等[9]进行了室内试验方面的研究。El-Sherbing[10]通过对双面加筋路堤的研究发现宽高比对两侧土压力分布有着较大影响。前人研究发现加筋形式不同，在地震荷载作用下，土压力大小和破裂面不同。对于高陡坡土工格栅加筋土堤不同厚高比在不同地震波作用下与位移、筋材受力函数关系的研究还未见相关报道。

以某高陡坡土工格栅加筋土堤项目为研究对象，采用Midas GTS NX软件进行有限元数值分析。在同一高度下，对不同土工格栅层间距的高陡坡土工格栅加筋土堤进行动力分析，建立不同地震波作用下任意高度处位移、筋材受力大小的计算方法，为高陡坡土工格栅土堤抗震设计提供理论依据。

1 工程概况

该高陡坡土工格栅加筋土堤工程坡面材料为加筋绿色格宾，坡体内采用HDPE单向塑料土工格栅，采用砾类土填筑。高度30 m的土堤长134.5 m，高度20 m的土堤长322.6 m，顶宽均为4 m，土堤两侧边坡坡率均为1∶0.364。其中30 m高坡体分三级填筑，如图1所示，20 m高坡体分两级填筑，如图2所示，台阶宽度均为2 m，整体平面图如图3所示。采用的单向土工格栅设计极限抗拉强度分别为37.8，28.9，20 kN·m-2。通过运土坡把砾类土运到填筑地点进行分层碾压，现已完工，如图4所示。

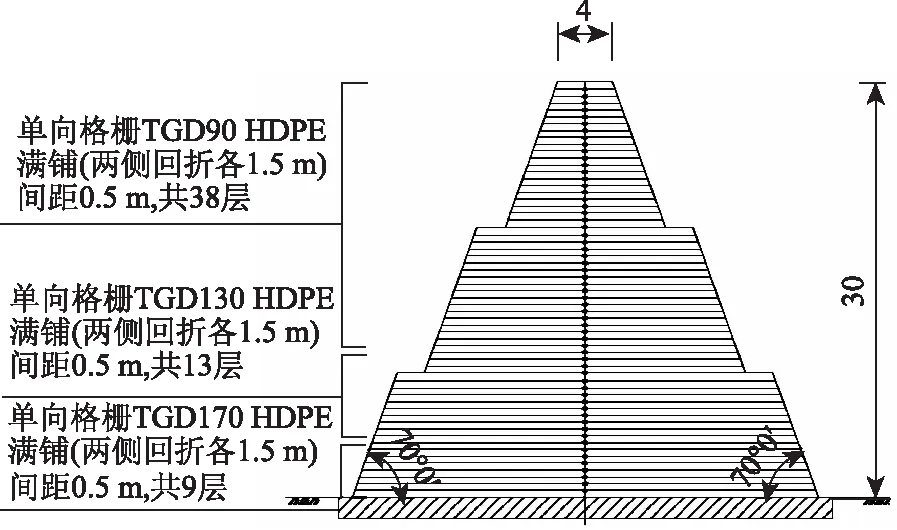
图1 三级土堤截面示意图(单位:m)Fig.1 Schematic diagram of 3-step earth embankment section (unit:m)

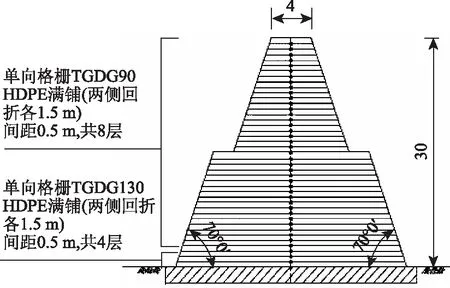
图2 二级土堤截面示意图(单位:m)Fig.2 Schematic diagram of 2-step earth embankment section(unit:m)

图3 整体平面图(单位:m)Fig.3 Overall plane(unit:m)

图4 高陡坡土堤Fig.4 An earth embankment on high steep slope

2 建立数值模型

2.1 模型建立

模型与实体工程比例为1∶1，分别建立填土层厚度0.4，0.5，0.6，0.7，0.8 m模型，其中0.5 m填土层厚模型是与实体工程填土厚度相同，如图5所示。为了得到不同模型在不同地震波作用下的位移和抗拉强度响应，每个模型上以A点为测点测位移，每层土工格栅中间单元为测点测抗拉强度。边界约束部分，地面以上无约束，地面以下为二维自由场约束。

图5 三维模型Fig.5 3D model

2.2 模型材料参数选取

材料参数如表1所示，材料参数通过项目地勘报告，类似土样与土工格栅复合体的大型三轴试验结果得到[11]。如表2中土工格栅的相关参数，通过土工格栅单向拉伸试验及筋-土界面特性试验测得。为了控制变量，建立模型时统一取土工格栅弹性模量3.7×107kN·m-2。

表1 材料参数Tab.1 Material parameters

2.3 阻尼设置及地震波选取

在地震加速度作用下，加速度较小时，土工格

表2 土工格栅截面和接触特性参数Tab.2 Geogrid section and contact characteristic parameters

栅应变很小，但阻尼依然存在，此时模型滞回圈过小无法得到阻尼特征[12]，所以采用瑞利阻尼修正这种不足，取阻尼比为0.05。震动周期T和频率f通过特征值分析得到，最大周期分别为5.023，最小为2.076，自由场建立在自然地基土的4个面上，约束为弹簧约束。

地震设防烈度为9度，8度，7度，6度，对应设计加速度分别为a≥0.4g，a≥0.3g，a≥0.2g，a≥0.1g，由于烈度6度地震响应小，所以对6度区不做分析[13]。在软件自带地震波型库中选取每个烈度所对应的相似加速，如表3所示。

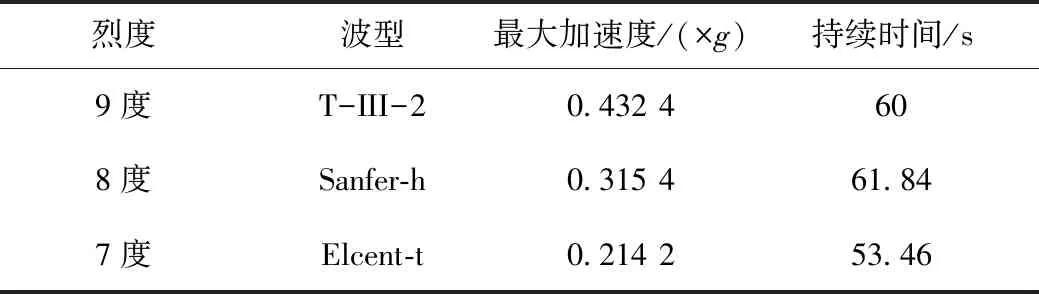
表3 地震波Tab.3 Seismic waves

上述3种地震波的地震加速度曲线a，b，c，如图6所示。进行数值分析时，选取地震波后把测点到导入历程分析中，每种地震波同时作用5个模型。

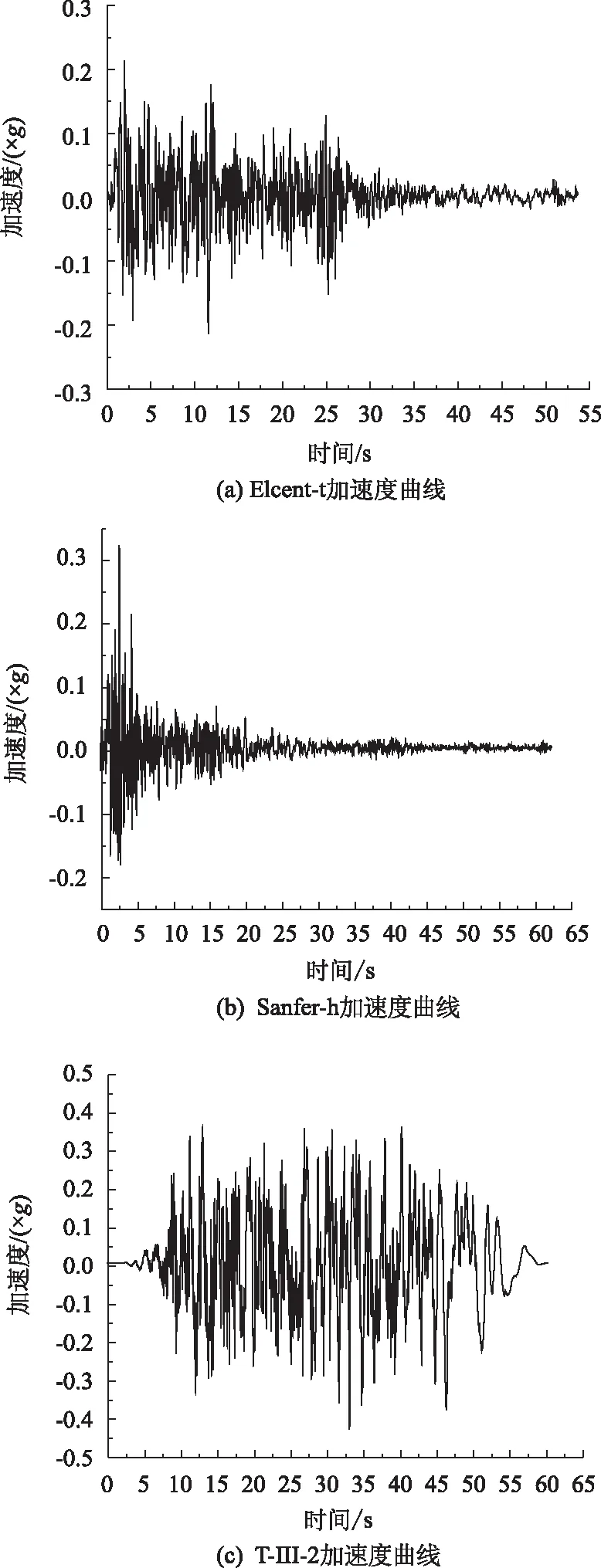
图6 地震波加速度曲线Fig.6 Acceleration curves of seismic wave

2.4 厚高比

在地震荷载作用下，除填土性质和土工格栅的抗拉强度及筋土作用参数外，土工格栅铺设层间距是结构位移和筋材受力的主要影响因素，也是结构设计的主要指标。为了研究在地震荷载作用下，土工格栅铺设层间距与位移以及筋材受力的关系，引入厚高比定义，即土工格栅铺设层间距与结构高度的比值，式(1)为结构总高度，式(2)为厚高比值e=h/H，其中填土的层厚就是土工格栅间距。本次有限元数值分析模型的厚高比如表4所示。

(1)

(2)

式中，hi为土工格栅厚度；hj为填土厚度。

表4 结构厚高比Tab.4 Structural thickness-height ratio

图7 地震响应加速度曲线Fig.7 Acceleration curves of seismic response

3 有限元结果分析

3.1 加速度分析

图7为3种不同地震波作用下不同厚度填土测点A的位移曲线d，e，f。可以看出结构响应加速度随着地震加速度的增加而增大，测点反应也越激烈，相同自由场下不同厚度填土加速度曲线和输入地震波的波型基本保持一致，并且厚高比越大加速度响应越大。在地震加速度作用下，填土层越厚意味着结构内部土工格栅对填土的约束力越小，填土就越自由，虽然填土材料参数相同，但是随着填土层厚的增加单层填土的质量也在增大，单位土工格栅所承受的应力越大，振动时的自由度也越大，因此在相同的地震波作用下，填土层的厚度决定了结构整体地震响应加速度大小。

3.2 放大倍数分析

地震加速度放大倍数除受高陡坡土工格栅加筋土堤高度影响外，还与填土层厚度有关。3种地震波作用下，不同填土厚度高陡坡土工格栅加筋土堤测点A处地震加速度放大倍数如表5所示，可以发现不同加速度作用下，测点A处的地震加速度放大效应不同。对于同一种地震波，土堤填筑层厚越大，结构对加速度的放大倍数越大；对于不同地震波，地震波的加速度越大，放大倍数越大。

表5 放大倍数Tab.5 Magnification

可见，在不同地震波加速度作用下，不同填土层厚加速度放大倍数有明显的差异，其原因除了各种地震波频谱特性有较大的差异外，还与填土层厚度有很大关系。填土层越小土工格栅层数越多，抗变形能力越强，结构刚度相应也越大，滤波消耗功率也越多，放大倍数相应也小。消耗功率可由式(3)表示[14]，消耗功率多少与土工格栅层数呈正相关。

(3)

式中,Dr为耗散功率;θ为旋转角;r为旋转角θ处对应的半径;φ为摩擦角;kt坡体内抗拉强度;v为速度。

3.3 水平位移分析

对3种不同地震波作用下，填土厚度0.4～0.8 m 共计5个模型进行数值分析，得到填土厚度与最大水平位移之间的关系如图8所示，可发现随着地震加速度和填土层厚度增大，测点A位移呈线性增长。不同加速度,地震波作用下，从下到上每一层填土中心节点处水平位移曲线，如图9所示，需要说明的是填土层厚度不同，对应的层数也不同。由图9可知，在地震加速度作用下各层填土水平位移均呈非线性增长，Elcent-t地震波作用在填土厚度为0.4 m的模型上时，位移变化率较小，T-III-2地震波作用在填土厚度为0.4 m的模型上时，位移变化率较大。

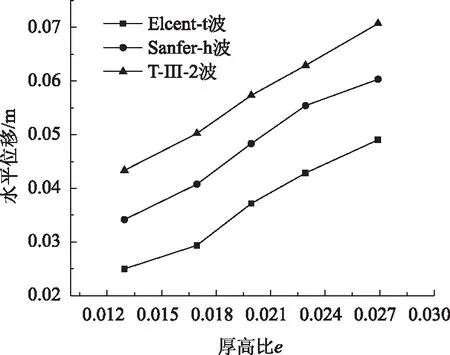
图8 最大位移曲线Fig.8 Maximum displacement curves

图9 加速度地震波曲线Fig.9 Acceleration seismic wave curves

图10为T-III-2地震波在最大加速度时刻作用0.8 m厚填土层的水平位移云图，可以看到此时结构有倾倒的趋势，但未发生整体破坏。图11为0.4 m厚填土层位移云图，在同一种地震波作用下0.4 m厚填土层与0.8 m厚填土层水平位移相比，前者明显小于后者，说明厚高比越小结构越稳定。

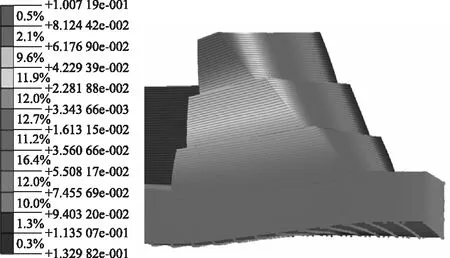
图10 0.8 m水平位移云图(单位:m)Fig.10 Nephogram of 0.8 m horizontal displacement(unit:m)

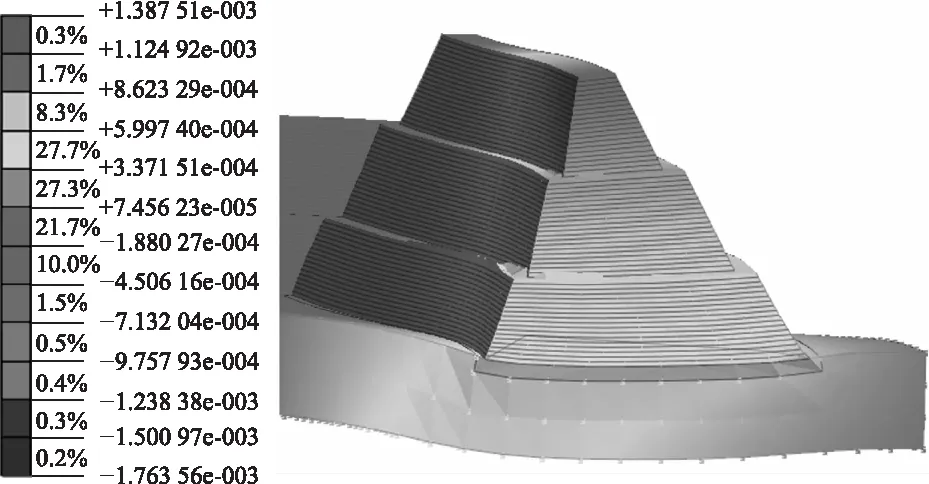
图11 0.4 m水平位移云图(单位:m)Fig.11 Nephogram of 0.4 m horizontal displacement (unit:m)

3.4 土工格栅受力分析

土工格栅受力监测点为每一层土工格栅接近模型中心的单元，地震波作用下，厚高比与土工格栅最大轴力之间的关系如图12所示，可得出随着地震加速度和填土层厚度增大，单元的最大轴力呈二次型增长模式。每层土工格栅在不同地震波作用下最大加速度时刻的轴力如图13所示，可以得出厚高比越大，在地震加速度作用下任意时刻的轴力越大，并且土工格栅轴力从下到上线性变小。因此，在土工格栅加筋土堤设计中为了保证良好的抗震效果，可采用上疏下密的布筋形式或在等间距布筋时，中下部应加大土工格栅的抗拉强度[11]。通过对土工格栅受力分析，可以看出发生7～9级地震时，土工格栅在极限抗拉强度范围内，不会出现断裂破坏，从而可以判断在该区段震级下结构不会发生整体性破坏，说明土工格栅加筋土堤作为一种柔性结构具有良好的抗震性能。

图12 最大轴力Fig.12 Curves of maximum axial force

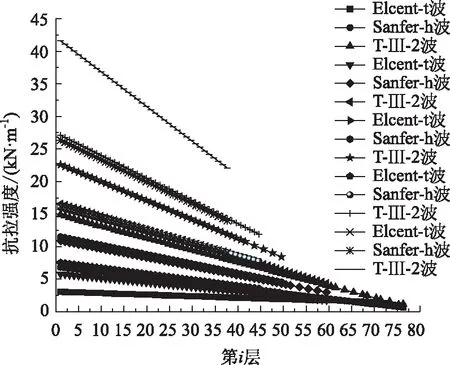
图13 每层土工格栅轴力云图Fig.13 Nephogram of axial force in each layer of geogrid

图14 0.4 m土工格栅受力云图(单位:kN)Fig.14 Nephogram of axial force in 0.4 m geogrid(unit:kN)

图15 0.8 m土工格栅受力云图(单位:kN)Fig.15 Nephogram of axial force in 0.8 m geogrid (unit:kN)

如图14和图15为T-III-2地震波加速度最大时刻，0.4,0.8 m填土厚土堤的土工格栅轴力分布云图，从云图中可以看出，0.4 m填土厚土堤的土工格栅轴力要比0.8 m的小，这是因为相同高度下土工格栅的层数越多填土层越多，每层填土的质量越小，分布在土工格栅上的压力越小，从而土工格栅受到的轴力也就越小。

加筋结构物通常抵抗竖向荷载的能力比抵抗侧向变形的能力强[15-18]。在地震作用下结构除了受到自身重力的影响外，还受到地震引起的惯性力作用，任意时刻，加速度的大小和方向在不断变化，惯性力方向及大小也不同，所以地震作用下结构内部土工格栅的内力分布并不均匀，即各层土工格栅的轴力沿格栅长度方向均呈现为非线性分布。

4 建立方程

4.1 任意时刻位移方程

曹建洲[12]等根据单自由度体系强迫振动理论来建立筋材最大位移方程，结合简谐荷载见式(4)：

FP(t)=Fsinθt。

(4)

作用有阻尼影响的微分方程，见式(5)：

(5)

求解任意时刻的动力位移，见式(6)：

y(t)=ypsin(θt-ϑ)。

(6)

振幅yp可用式(7)表示：

(7)

式中，ξ为地震作用的效应折减系数；yp为振幅；yst为荷载最大值F静力作用下位移；w为固有频率；β1为动力系数；θ为荷载频率；ϑ为相位移。

简谐荷载有规律可循，有些动荷载不是简谐荷载，但是具有周期性，可通过富士系数展开，可进行无限个简谐荷载叠加得到规律。地震波为不规则荷载，无规律可循，此时式(6)计算任意时刻的动力位移不适用，就需要改进。式(4)可以变化为式(8)，由式(8)得到不规则地震加速度曲线下地震振幅峰值曲线。

(8)

式中，Fp(t)为地震振幅峰值；ai为任意时刻加速度；ti为任意时刻。

得到变化后有阻尼影响的微分方程，见式(9)：

(9)

则变化后任意时刻的位移见式(10)，从而得到不规则地震荷载下任意时刻位移。

(10)

4.2 建立任意高度的位移方程

地震加速度作用下任意时刻不同高度水平位移不同，为了得到任意高度的水平位移，结合任意时刻位移式(10)，并且假设此位移为结构最高处某点位移，得到的测点运动轨迹为圆弧，为了方便计算可把弧线看作直线y(t)，如图16虚线为结构整体位移。图17为位移几何关系，其中L垂直高度H，测点绕平衡O点转过的长度为y(t)，转角为θ，θ如式(11)表示。

。

(11)

图16 位移示意图Fig.16 Schematic diagram of displacement

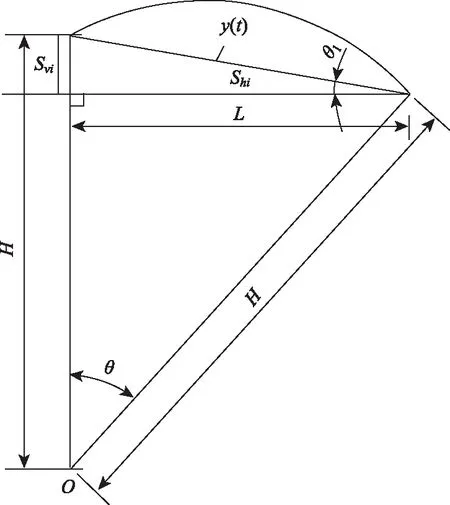
图17 位移几何Fig.17 Displacement geometry

由图17几何关系得任意高度水平位移如式(12)：

(12)

式中,Shi为任意时刻水平位移；Hi为任意高度。

根据式(12)水平位移和几何关系可得到垂直位移，见式(13)：

(13)

式中，Svi为任意时刻垂直位移。

4.3 潜在滑裂面的位置

地震惯性力可分为垂直分量和竖直分量，分别由式(14)和式(15)表示[19]，采用拟静力法进行动力作用时土工格栅受力状态，如图18所示。从图中可以看出土工格栅轴力大小由惯性力和重力决定，由于结构不规则有些部位惯性力大，有些部位小，轴力的大小相差也较大，图中B为填土的受力状态，A点就是土工格栅某时刻地震作用下的受力状态，也是土工格栅上最大力的集中点，每一层土工格栅都有一个最大轴力点，这些最大轴力点的连线接近圆弧形状，由此可以得出此圆弧就是发生地震时的潜在滑裂面。

Fhi=ahξWiαi/g，

(14)

Fvi=ahξWiαi/(3g)，

(15)

式中，Fhi为水平惯性力；Fvi为竖向惯性力；Wi为集中于测点i的土条重力；ah为水平方向设计地震加速度；αi为测点i的动态分布系数。

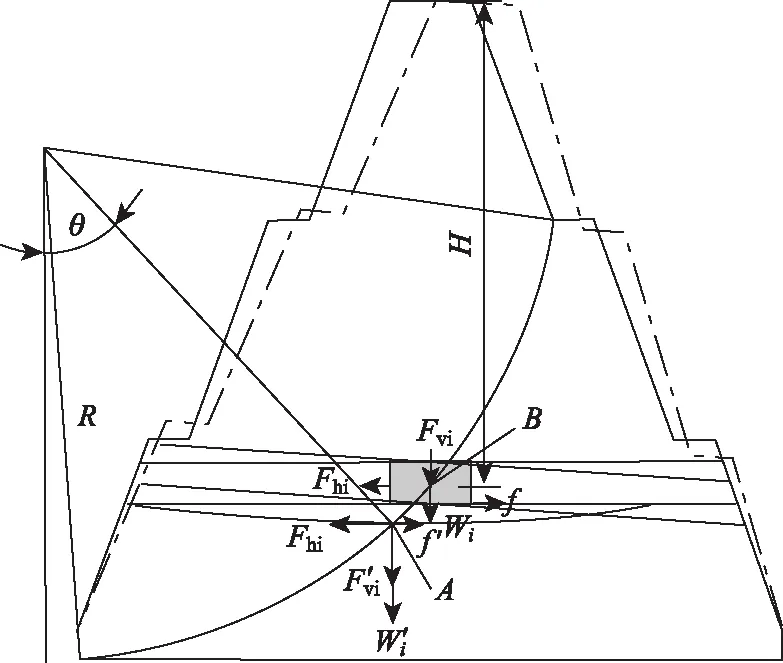
图18 土工格栅轴力分布Fig.18 Distribution of axial forces in geogrid

4.4 建立任意层土工格栅拉力方程

建立公式(16)来表示每层填土的质量在单位长度土工格栅上拉力[20]。从总体受力情况来看随着地震加速度的增大筋材受力增大，因为随着加速度的增大结构的惯性力也在增大，同时土工格栅抵抗惯性力的能力也随着提高。

Ti=ERεRtb=mig，

(16)

式中，Ti土工格栅拉力；ER为土工格栅变形模量；εR为最下层土工格栅的应变；tb为土工格栅截面积；mi为某层填土的质量。

图19为土工格栅A点地震时的受力状态，该受力考虑下层填土对土工格栅的支撑力，其压力和支撑力的合力为W′i，并且假设土工格栅两端固定。

图19 A点受力状态Fig.19 Stress state at point A

第i层土工格栅所受土层的重力为第i层以上所有土层的重力之和，如式(17)所示。因为填土层为梯形如图20所示，由填土层几何形状可得每层填土的自重应力，如式(18)所示。

图20 填土层几何形状Fig.20 Fill layer geometry

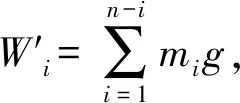
(17)

(18)

式中,W′i为填土重力Wi作用在土工格栅上的压力;n为总层数;γ为土的重度;θ1为坡角。

合力所围成的夹角β大小如式(19)所示：

(19)

式中，F′hi为作用在土工格栅上水平惯性力;F′vi作用在土工格栅上垂直惯性力。

由此可以得到地震作用下任意层某一点土工格栅合力如式(20)所示，式(21)适用梯形几何土层土工格栅合力计算:

(20)

(21)

5 理论计算的数值验证

5.1 位移和抗拉强度验证

为了验证理论计算的正确性，首先算得在T-III-2 波最大加速度时刻转角θ为0.014 2°，然后分别计算0.027厚高比下，填土每一层中心处位移及土工格栅单元的抗拉强度、位移和抗拉强度的计算值与数值分析值对比，如图21、图22所示，从图中可以得到理论计算结果和模拟结果趋势大致一致。

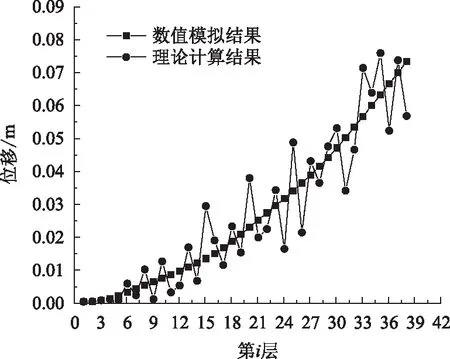
图21 位移对比Fig.21 Comparison of displacements

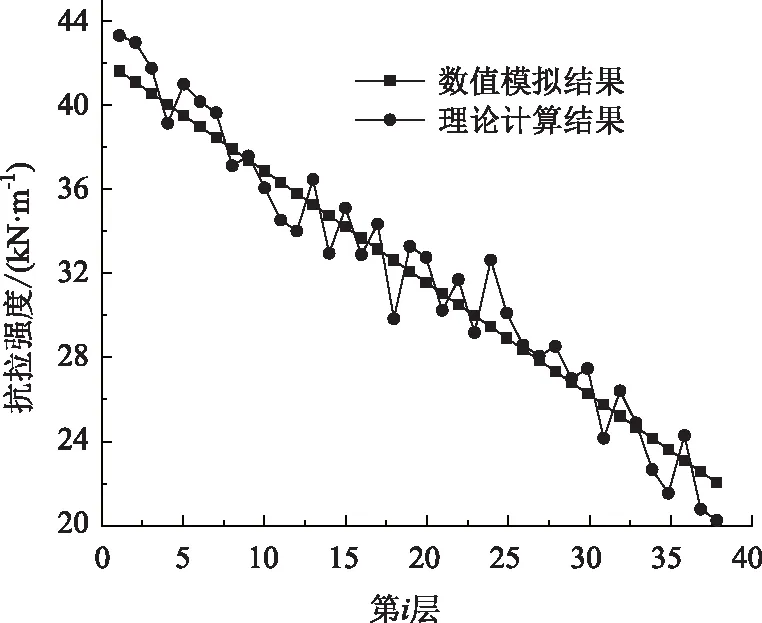
图22 抗拉强度对比Fig.22 Comparison of tensile strengths

6 结论

(1)高陡坡土工格栅加筋土堤厚高比越小结构耗散的地震动力能量越多，抗震性越好，相反越大，抗震性越差。厚高比越大地震加速度下位移和土工格栅受力越大，相反越小，位移和土工格栅受力越小。在土工格栅加筋高陡土堤设计中为了保证良好的抗震效果，可采用上疏下密或等间距的布筋形式。

(2)随着地震加速度和厚高比的增大，土工格栅单元的最大轴力呈二次型增长模式，从上到下每一层填土中心附近土工格栅轴力线性减少。不同地震加速度下不同厚高比土堤水平位移呈非线性增长模式，从上到下每一层填土中心处的位移呈二次型增长。

(3)在地震作用下土工格栅受力大小与惯性力有密切的关系，土工格栅由惯性力决定。通过每一层土工格栅上受力最大点的连线，可以得出地震荷载作用下的潜在滑裂面。通过理论计算值与模拟值对比，发现二者的结构位移值、土工格栅抗拉强度值较接近，说明理论计算具有一定的合理性。