塔梁连接方式对多塔悬索桥地震反应的影响

郑锋利,陈逸民,李建中,徐之文

(1.温州瓯江口大桥有限公司,浙江 温州 325002， 2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

0 引言

随着我国交通与经济的发展，大跨度桥梁的建设也越来越多，其中悬索桥以缆索为主要承重构件，是目前跨越能力最强的桥型。相对于传统的两塔悬索桥或者自锚式悬索桥，三塔悬索桥可实现连续长大跨越，突破单一跨径的限制。我国现已建成的泰州长江大桥、瓯江北口大桥均为世界级三塔四跨悬索桥。

悬索桥的塔、梁、墩之间的连接方式对桥梁抗震性能有很大的影响[1-4]。目前世界上已建成的多塔悬索桥中，主要采用的塔梁连接体系有：主梁纵向无约束体系(主梁与塔、边墩间仅采用纵向活动支座)，中塔固接体系(主塔与中塔固接，主梁与边塔、边墩间无约束)，以及上述体系附加纵向约束装置(如阻尼器或弹性连接)的组合体系。对于缆索支承桥梁合理的纵向减振体系，科研人员和结构工程师进行了广泛而深入的研究[5-7]，既有研究表明：中塔固接体系主塔内力响应较大，梁端纵向位移较小，主梁纵向无约束体系能够改善桥塔的内力，但存在主梁纵向位移过大的问题，为改善悬索桥在静力、动力下的结构响应，悬索桥常采用附加纵向约束装置的组合体系。

在塔、梁间设弹性连接装置或阻尼器等是控制梁端位移的主要措施[8-14]，国内外许多桥梁应用了此类装置。叶爱君等[15]研究了流体黏滞阻尼器连接体系对超大跨度斜拉桥地震反应的影响。邬都[16]等以虎门二桥为背景，研究了双塔悬索桥抗震体系中黏滞阻尼器的减震效果，结果表明桥梁梁端位移和主要构件的内力都有显著改善。邓育林等[17]研究了在三塔悬索桥中塔处设置弹性索对多塔悬索桥地震反应的影响，结果表明：应用弹性索明显减小了主梁梁端位移、主梁与次边跨间相对位移以及边塔弯矩，但中塔内力反应影响不大。易凌志[18]等以国内某大跨混合梁斜拉桥为例，研究得出近断层地震作用下，选用阻尼器体系或者组合体系相较于弹性连接体系，减震效果更为理想。

为探究多塔悬索桥合理的抗震结构体系及阻尼器装置对悬索桥抗震的影响，本研究以一座三塔悬索桥为背景，分析研究了中塔塔梁固接体系、主梁纵向无约束体系及设置黏滞阻尼器组合体系的地震响应特点，并进行了黏滞阻尼器参数分析。

1 背景工程与地震动输入

本研究以温州瓯江北口大桥为背景进行研究，温州瓯江北口大桥连接温州乐清与瑞安，是浙江省甬台温高速公路复线温州乐清至瑞安段和温州市南金公路上的控制工程，主桥采用(230+2×800+348)m三塔公铁两用悬索桥方案，桥梁全长2 178 m，矢高78.82 m，矢跨比为1/10.15。两主跨跨越主航道及副航道。全桥总体布置图见图1。

瓯江北口大桥主梁为钢桁梁，上层两幅为高速公路车道，下层两幅为南金公路车道，中间为铁路轨道。中塔为钢筋混凝土A型主塔，南北两边塔为门型塔；中塔采用沉井基础形式，南北边塔采用群桩基础。梁体与中塔、边塔和边墩之间采用纵向活动支座，无约束；横桥向主梁与中塔、边塔和边墩间采用固接。

图1 瓯江北口大桥主桥立面图(单位：cm)Fig.1 Elevation of main bridge of Oujiang River North Estuary Bridge (unit: cm)

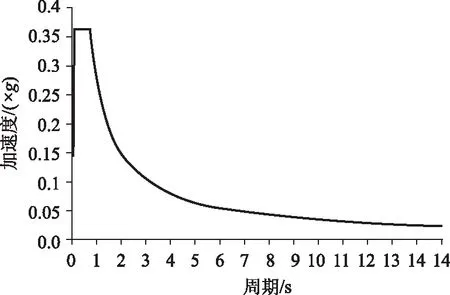
图2 地震动加速度反应谱(阻尼比0.02)Fig.2 Response spectrum of ground motion acceleration (damping ratio: 0.02)

针对场地特点，提供的瓯江北口大桥主桥50 a超越概率2%的水平向地震动加速度反应谱(2%阻尼比)如图2所示。其中，竖向地震荷载取为水平地震荷载的0.65。

在进行非线时程分析时，以场地50 a超越概率为2%水平下的水平加速度反应谱(阻尼比取2%)为目标谱拟合了7条水平时程波，计算结果取7条地震动输入下的平均结果。

2 动力模型与动力特性

根据瓯江北口大桥主梁的特点，建立的空间动力模型如图3所示。

图3 悬索桥的有限元计算模型Fig.3 Finite element model of a suspension bridge

在建立空间动力模型时，采用空间梁单元模拟主桥加劲梁、主塔、边墩，采用杆单元模拟主缆和吊杆。建模时考虑了恒载几何刚度对主缆、吊杆和主塔的影响。荷载方面主梁桁架和二期恒载在梁单元上以线质量形式施加。按刚体近似模拟桩基础承台，承台质量设置在质心处。考虑到中塔采用沉井基础，中塔塔底采用固接，边塔和边墩采用桩基础，在承台底加6个方向的弹簧来模拟桩基础的作用。

为了研究黏滞阻尼器的减震效果，本研究在进行不同约束体系比较时，将黏滞阻尼器的参数设置为变量。黏滞阻尼器的阻尼力取决于塔梁间的相对速度，它们之间的关系可表达为：

F=C·Vα，

(1)

式中，α为阻尼指数(阻尼指数范围一般取0.1～2.0)；C为阻尼系数。

对于阻尼器的基本参数，阻尼系数C影响阻尼器的阻尼力和耗能能力，阻尼指数α决定黏滞阻尼器的非线性特征，当阻尼指数α=1.0时，阻尼器为线性阻尼器，式(1)退化为F=C·V；当阻尼指数α=0时，阻尼器为纯摩擦阻尼器，相应的式(1)退化为F=C。阻尼指数α对阻尼力的影响趋势取决于塔梁间的相对速度，当相对速度V<1.0 m/s时，阻尼力随指数减小而增大，当相对速度V>1.0 m/s时，阻尼力随指数α增大而增大。

表1为采用所建立的空间动力模型计算出的主桥前10阶振动周期和振型特征。顺桥向累计参振质量达到95%时所需要选取的振型数量为910阶，对应周期为0.056 s；横桥向累计参振质量达到95%时所需要选取的振型数量为922阶,对应周期为0.048 s；竖向累计参振质量达到95%时所需要选取的振型数量为950阶,对应周期为0.028 s。由表1可以看出，瓯江北口大桥的第一阶振型为横向反对称振动，周期为9.805 s；第二阶振型为主梁纵向振动，振动周期为9.636 s。

表1 计算模型基本动力特性Tab.1 Basic dynamic characteristics of calculation model

注：振型描述和振型图如下所述，其中名词“一阶”为单跨内的形状特征，“正对称”或者“反对称”为针对两跨的形状特征。

3 塔梁连接方式对地震反应的影响

为了比较多塔悬索桥纵桥向主梁与塔、墩连接关系对结构地震响应的影响，本研究针对以下5个工况进行研究：

(1)工况1：纵桥向，主梁与塔、边墩间无约束(仅采用纵向活动支座)，本研究称主梁纵向无约束体系；

(2)工况2：纵桥向，主梁与中塔固接，主梁与边塔、边墩间无约束，本研究称中塔固接体系；

(3)工况3：在工况1的基础上，主梁与中塔、边塔采用黏滞阻尼器，并对黏滞阻尼器的参数进行分析；

(4)工况4：在工况2的基础上，主梁与两座边塔处采用黏滞阻尼器，并进行黏滞阻尼器的参数分析；

(5)工况5：在工况1的基础上，主梁与两座边塔处采用黏滞阻尼器，并进行黏滞阻尼器参数分析。

3.1 主梁纵无约束体系与中塔固接体系

表2为采用非线性时程方法计算出的主梁无约束体系和中塔固接体系结构地震响应。由表2可以看出，对于主梁的梁端位移，中塔与主梁固接体系位移为0.543 m，相对较小，而对于中塔塔底响应，中塔与主梁固结体系的塔底弯矩、剪力分别为半漂浮体系的1.32倍和1.21倍。对于边塔塔底响应，两种体系差别不大。

3.2 梁体与主塔、边塔均采用阻尼约束

工况3为在主梁纵无约束体系的基础上，3个桥塔处均设置阻尼器。由于桥梁是纵向非对称悬索桥，故选取了中塔、北边塔、南边塔的塔底内力响应进行比较。在对阻尼器参数进行分析时，阻尼指数α取0.3，阻尼系数C分别取1 000，3 000,5 000,7 000,9 000(阻尼系数C的单位为kN/(m/s)0.3)。

图4(a)～(c)分别为梁端位移、塔底剪力、塔底弯矩随阻尼器参数变化图，图4(d)为阻尼器阻尼力和塔梁间相对速度随阻尼器参数变化图。

表2 主梁纵无约束及中塔固接体系主要地震响应Tab.2 Main seismic response of system of longitudinal unrestricted main girder and fixed middle pylon

由图4可以看出，设置阻尼器时主梁梁端位移显著减小。当阻尼系数C增加，主梁位移减小，塔梁间相对速度减小，阻尼力呈线性增加，而各塔塔底弯矩和剪力虽然有所减小，但减小幅度不大。一般在罕遇地震下要求桥梁的主梁梁端位移控制在30 cm 以内，考虑到阻尼器参数增大会导致建设成本明显增多，阻尼器参数设置为α=0.3，C=9 000 kN/(m/s)0.3较为经济合理。

3.3 中塔固接边塔设置阻尼约束

工况4为在中塔固接体系基础上，两座边塔处均设置阻尼器。针对这种塔梁连接方式，边塔阻尼器参数取值与工况3相同。阻尼器系数C对主梁梁端位移、塔底剪力、塔底弯矩、阻尼力的影响见图5。

图4 工况3的地震反应随阻尼器参数变化图Fig.4 Seismic response varying with parameters in case 3

图5 工况4的地震反应随阻尼器参数变化图Fig.5 Seismic response varying with damper parameters in case 4

由图5(a)可以看出， 当阻尼系数大于3 000 kN/(m/s)0.3后，主梁位移迅速减小到0.3 m以下，然后逐渐减小。可以看出，中塔固结的塔梁连接方式，梁端位移相对于漂浮体系梁端位移较小，并且设置边阻尼器也起到了很好的限位作用。此外，与全阻尼器体系对比，中塔固接并设置边阻尼器的结构体系，边塔塔底反应略有减小。

由图5(a)～(c)还可以看出，主梁位移随阻尼系数增大而减小，但当阻尼系数C达到一定值时，主梁位移变化速率减缓，且各塔塔底弯矩趋势缓慢，考虑到过大的阻尼系数会导致较高的成本，因此推荐的阻尼器参数为α=0.3，C=3 000 kN/(m/s)0.3。

3.4 仅边塔设置阻尼约束

采用半漂浮体系，在两个边塔处均设置阻尼器， 对边塔阻尼器进行参数分析，边塔阻尼器参数对主梁位移、塔底剪力、塔底弯矩及阻尼力的影响见图6。

图6 工况5的地震反应随阻尼器参数变化图Fig.6 Seismic response varying with damper parameters in case 5

由以上分析结果可看出，中塔放开，在边塔设置阻尼器时的地震响应与全阻尼器时的地震响应变化规律基本一致。对比可以看出，在边塔处设置阻尼器与全阻尼器体系相比，主梁位移稍微大一些，塔底弯矩的变化趋势相似，由此可以得到，中塔处不设阻尼器时与设置阻尼器时结构的内力、变形无明显变化。

对比各结构体系下地震响应结果如表3所示，阻尼器参数取推荐值。

表3 多塔悬索桥各结构体系下的地震反应比较Tab.3 Comparison of seismic responses of multi-pylon suspension bridges under each structural system

由表3可知，中塔固接，边塔放开体系的中塔塔底弯矩最大；与半漂浮体系相比，设置阻尼器的3种结构体系主梁梁端位移及中塔塔底弯矩均显著减小，边塔塔底弯矩差别不大；中塔固结可减小梁端位移，但相应的塔底地震响应会增大；当不考虑经济成本时，中塔固接，边塔设置阻尼器的结构体系地震响应相对较小。中塔放开，边塔设阻尼器体系与全阻尼器体系相比，中塔与边塔塔底处弯矩和剪力基本相同，但梁端位移较大，可考虑适当提高边塔处阻尼器的阻尼系数C。

4 结论

多塔悬索桥的塔、梁、墩之间的连接方式对桥梁地震响应有显著影响，选取合理的结构形式可有效控制地震反应。本研究通过比较不同方案下的桥梁位移和内力，研究了多塔悬索桥的合理抗震结构形式，并对黏滞阻尼器进行了参数分析，主要结论如下：

(1)中塔固接体系多塔悬索桥的梁端位移可以得到有效控制，但其中塔受力最为不利，可考虑调整中塔与边塔的合理刚度比，从而提升结构受力效率。

(2)相较于主梁纵向无约束体系，设置黏滞阻尼器可显著减小多塔悬索桥的地震响应，梁端位移得到有效控制，且塔底地震响应也略有减小。阻尼系数C影响减震效果，当阻尼系数增大时，结构地震响应可显著减小。

(3)由于黏滞阻尼器随塔梁间相对速度变化的规律呈非线性特征，对阻尼器进行参数研究十分必要。优化阻尼器参数时，需要综合考虑悬索桥地震下的主梁位移、主塔塔底受力以及阻尼器的造价和性能。

(4)对于中塔固接，边塔设置阻尼器的体系，随着阻尼系数的增加，当阻尼系数C超过一个定值时，主梁位移减小趋势变缓，考虑到造价和效益，阻尼器参数可参照这个数值进行设置。

(5)中塔放开，边塔设置阻尼器体系结构的受力、位移与全阻尼体系基本一致，因此，在保证结构安全的情况下，可适当考虑中塔处放开，依靠边塔阻尼器和纵向滑动支座来限制主梁位移。

(5)对于中塔固接，边塔设阻尼器体系，当阻尼器参数较小时，减震效果不明显，主要依赖中塔固接来限制梁端位移，相应的中塔塔底响应略大。阻尼器参数的合理取值也受到结构自身刚度的影响，而当结构的位移越小，则必有一处内力增大，选取合理的结构体系和阻尼器参数就是使桥梁抗震的各个效应达到一个均衡的最优解。