智能汽车测试工况与用户工况关联评价模型

李文亮，周 炜，宋 毅，张 禄，张金玲

(1. 交通运输部公路科学研究院 运输车辆运行安全技术交通行业重点实验室，北京 100088； 2.北京邮电大学，北京 100876)

0 引言

智能汽车是当前全球汽车与交通领域发展及研究的前沿热点，是各国争抢的战略制高点[1-2]。为了保障智能汽车安全上路，需要在试验场内开展大量测试来验证智能汽车功能和性能。尽管在国内外已经开展了相关标准和体系的研究和制定[3-5]，但缺少对试验场测试工况与用户工况关联评价模型开展研究。

周炜[6-7]等开展了汽车试验场可靠性道路试验仿真与搓板路强化系数研究，为汽车可靠性强化道路试验规范的制定、验证和优化提供依据。祝安定[8-10]等基于雨流计数研究汽车试验场路面强化关系。于海波[11-13]研究了针对传统汽车试验场可靠性试验技术规范存在的问题，提出了一种与用户用途关联的汽车可靠性试验方法。Elgharbawy M[14-15]等介绍了智能汽车自适应功能测试的基本原理，包括常用的验证和验证过程。

本研究基于人-车-路协同的行车风险场的概念[16]，建立智能汽车测试工况与用户工况关联评价模型，结合算例对所建立的关联模型进行分析。

1 理论研究

1.1 危险度模型

危险度模型如下所示[9]。

(1)

Fj=Es_jMjRjexp[-k2vjcosθj](1+Drj)，

(2)

式中，Es_j为物体j位置处的场强合矢量；ER_j、EV_j、ED_j分别为势能场、动能场、行为场在物体j位置处的场强合矢量；Fj为车辆j当前行车状态的危险程度；Mj为物体j的等效质量；Rj为(xj,yj)处的道路条件影响因子；k2为大于零的待定常数；vj为物体j的速度；θj为物体j速度方向与Ej方向的夹角；Drj为车辆j中驾驶人的驾驶风险因子。

1.2 匹配模型

以危险度进行匹配，用户危险度求和量与试验场求和量一致，如式(3)所示。

∑[Xi][Hi]=∑[Yj][Lj],

(3)

式中，Xi，Yj分别为用户和试验场的不同危险度；Hi，Lj分别为Xi,Yj所对应的工况次数。

匹配模型提出3个原则：

(1)尽量涵盖最大危险度；

(2)减少小危险度的次数，增加大危险度的次数，实现加速；

(3)危险度-工况次数分布曲线尽量接近。

1.3 评价模型

评价原则采取以下4个影响因素：(1)危险度分布相似性，相似性越大越好；(2)加速系数，加速系数越大越好；(3)最大危险度，越接近用户极限值越好；(4)样本危险度覆盖率，危险度覆盖率越大越好。

工况危险度分布相似性定义为两条曲线距离均方根的倒数，表示为r：

(4)

式中，R为用户和试验场工况次数-危险度曲线的距离均方根;y，y′分别为用户和试验场曲线中，相同横坐标下的纵坐标。

样本危险度覆盖率ε表示为：用户数据中各个危险度区间内工况次数所占总工况次数的百分比与其对应系数φi的乘积再求和：

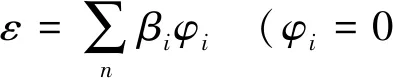
(5)

式中，βi为用户数据中各个危险度区间内工况次数所占总工况次数的百分比，对应系数为φi为0或1，当测试规程在危险度区间i中存在工况，则φi为1，否则为0。

加速系数η表示为用户工况次数总和与试验场工况次数总和之比：

(6)

最后采取有效性指数作为综合评价模型，按照有效性指数对不同测试规程的优劣性进行排序。有效性指数=加速系数/加速系数的和+危险度覆盖率/危险度覆盖率的和+最大危险度/最大危险度的和+危险度分布相似性/危险度分布相似性的和，再将4个影响因素分别乘以各自所分配的权重，即：

(7)

式中，λi为有效性指数；ci,ki,fi,si分别为加速系数、危险度覆盖率、最大危险度、危险度分布相似性；ac,ak,af,as分别为4个影响因子的权重系数。

2 实际算例分析

2.1 模型应用

图1为两车沿道路中心线同向行驶的工况[9]。

图1 两车沿道路中心线同向行驶工况Fig.1 Working condition of 2 vehicles drive in same direction along road centerline

用户实际工况采用某企业提供的某城市2012 年全年的交通事故数据中部分追尾事故工况数据[3]。危险度计算结果，两车速度以及对应的工况次数在表1中详细给出。

2.2 用户实际工况数据

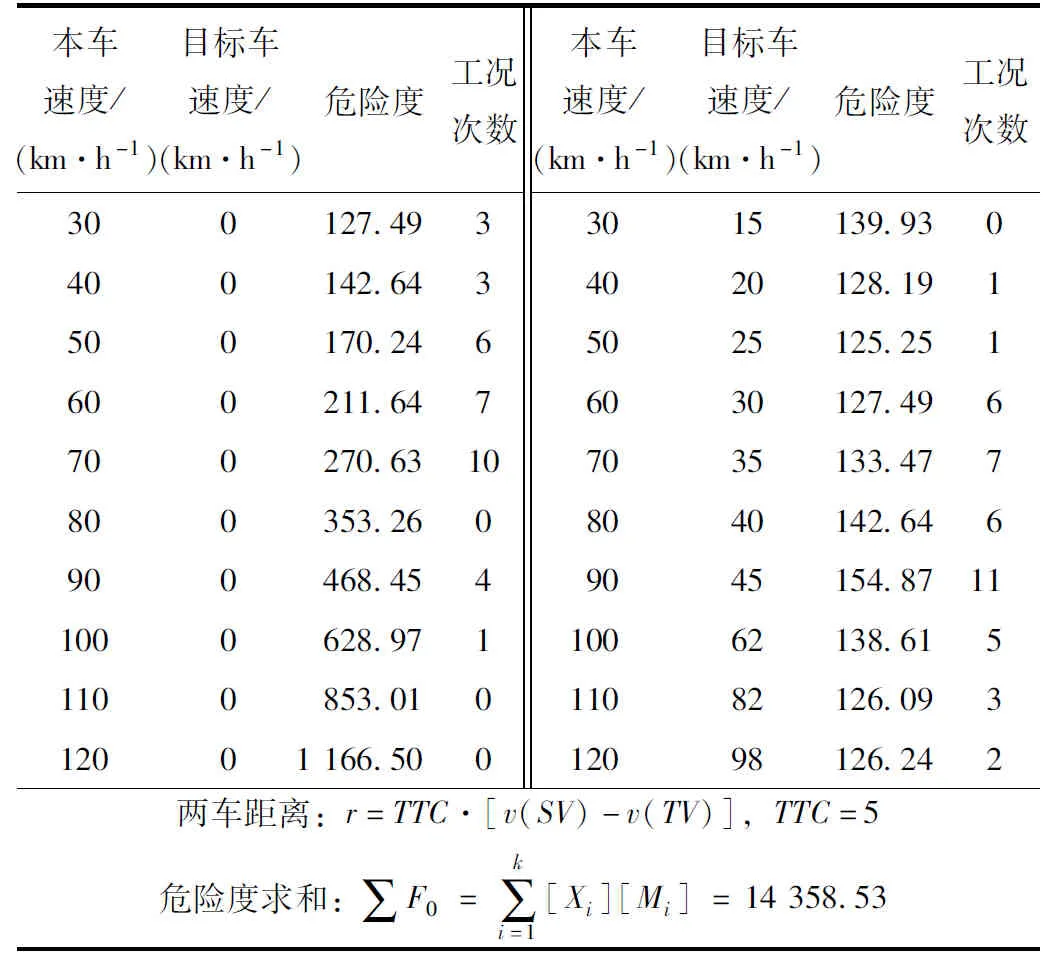
表1 用户工况次数分布Tab.1 Frequency distribution of user’s working conditions

将工况次数的危险度分布用直方图区间来表示，如图2所示。

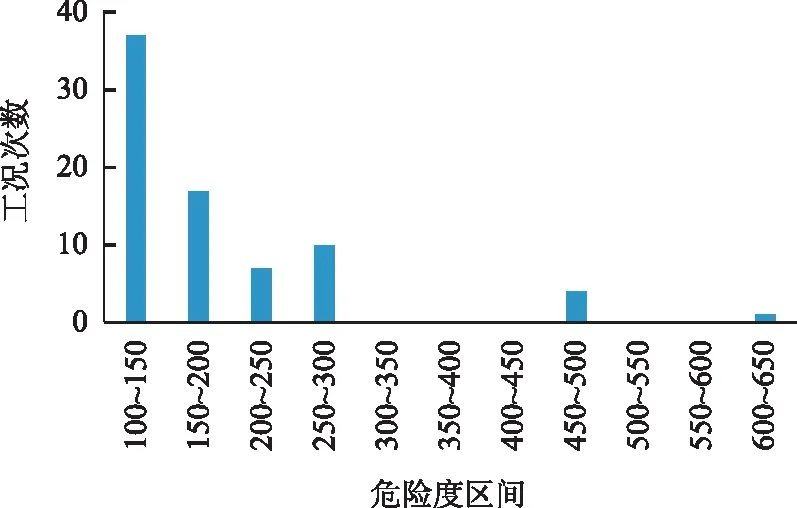
图2 用户危险度区间-工况次数直方图Fig.2 Histogram of user’s risk degree interval vs. frequency of working conditions

2.3 试验场工况数据

参考JT/T 1242—2019、GB/T 33577—2017、ISO 22839标准[4,17-18]，给出表2～表4这3个测试规程。

表2 测试规程1工况次数分布Tab.2 Frequency distribution of working conditions in test procedures 1

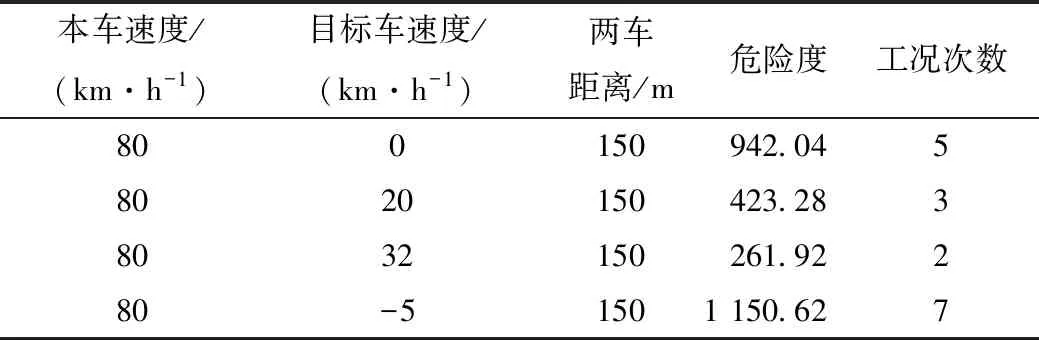
表3 测试规程2工况次数分布Tab.3 Frequency distribution of working conditions in test procedures 2

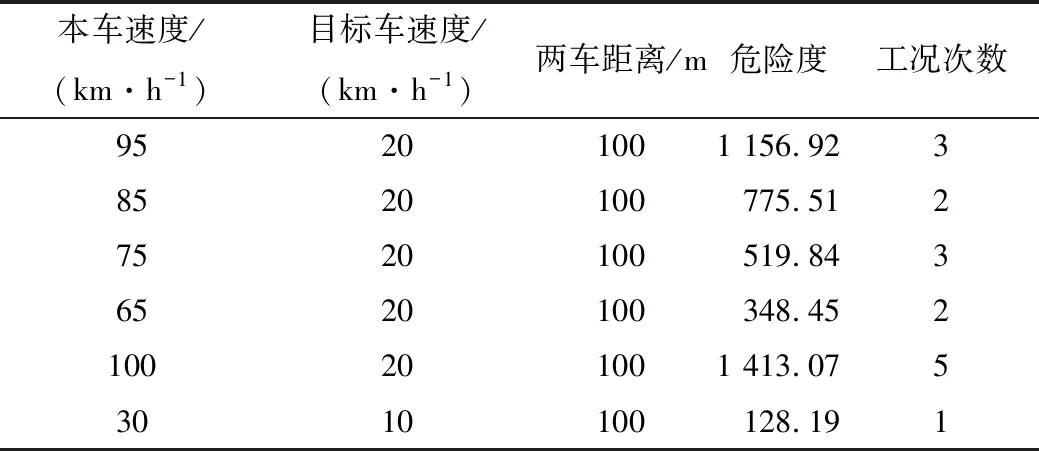
表4 测试规程3工况次数分布Tab.4 Frequency distribution of working conditions in test procedures 3

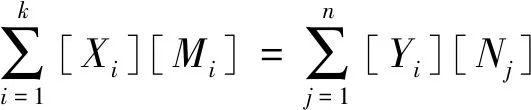
图3为用户与3个测试规程的危险度-工况次数分布曲线对比。

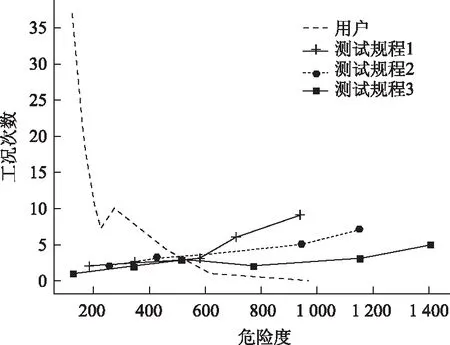
图3 危险度-工况次数分布图Fig.3 Curves of risk degree vs. frequency distribution of working conditions

可以看出，测试规程与用户数据相比，均减小了小危险度的工况次数，增加了大危险度的工况次数，从而达到加速试验以及危险度匹配的要求。下面从加速系数、样本危险度覆盖率、最大危险度、危险度分布相似性4个方面来计算3个测试规程的有效性指数，从而评估3个测试规程的优劣。

2.4 有效性评估

有效性指数可以根据式(6)求得。其中加速系数的计算由式(5)给出，加速系数的值为用户工况次数总和与试验场工况次数总和之比，用户工况次数由表1给出，总数为76次；各个测试规程的工况次数在表2～表4中已经给出，分别求和即可得到。

危险度覆盖率的计算由式(4) 给出，先求出用户数据中各个危险度区间内工况次数所占总工况次数的百分比，再对照每个测试规程涵盖的危险度落到了哪些区间，将这些危险度区间所对应的百分比叠加即可得到危险度覆盖率。

最大危险度的值取每个测试规程中危险度最大的数值。危险度分布相似性的计算由式(3)给出，先求出用户和试验场两条曲线垂直方向上的距离均方根，再取倒数即可得到。各测试规程的4个评价指标以及有效性指数的计算结果如表5所示。

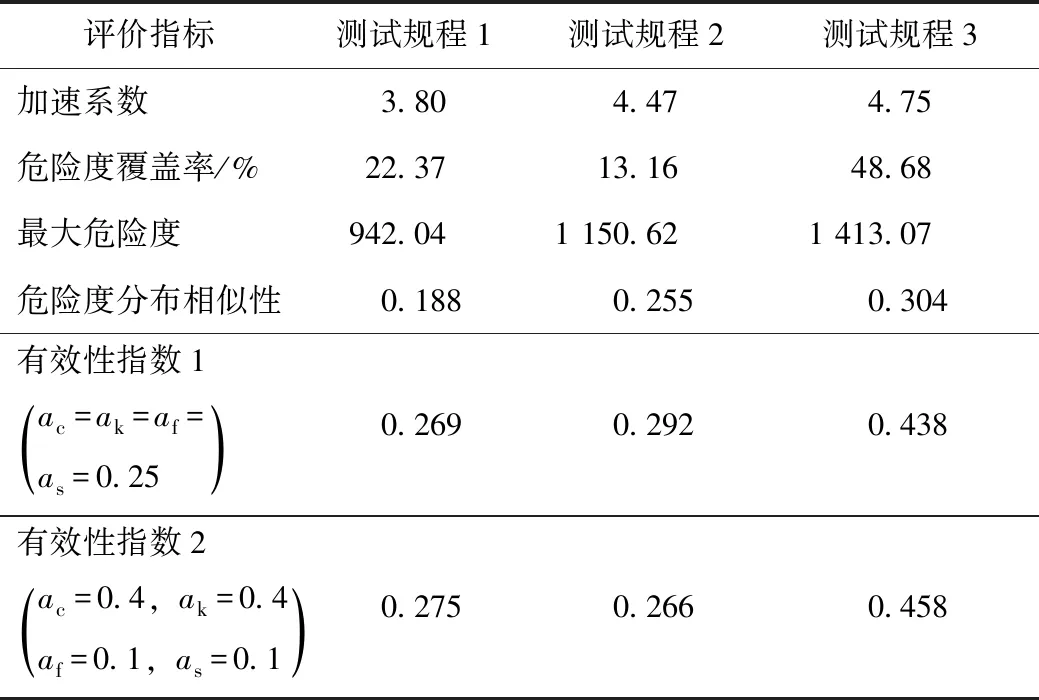
表5 各测试规程有效性指数对比Tab.5 Comparison of effectiveness indicators in different test procedures

当4个影响因素的评价指标权重分配相等时，即当ac=ak=af=as=0.25时，测试规程3的有效性最高，规程2次之，规程1有效性最低。可以看出测试规程3的4个评价指标均高于测试规程1和2，尤其是危险度覆盖率和最大危险度两个指标上明显大于前两个规程。

测试规程中如果需要更多考虑到更大的加速系数以及更大的样本危险度覆盖率，可以将权重重新分配，即当ac=0.4,ak=0.4,af=0.1,as=0.1时，测试规程3的有效性最高，规程1次之，规程2有效性最低。可以看出改变了权重分配之后，测试规程1和2的大小关系发生了变化。在加速系数和危险度覆盖率权重较高时，测试规程1的有效性优于测试规程2。

权重的分配会在一定程度上影响最后的评价结果，如果在测试过程中有不同的需求，可以根据需求来调整4个评价指标的权重。

3 结论

(1)首次建立了智能汽车测试工况与用户工况的关联模型，通过“危险度”建立了测试工况与用户工况内在的理论关联关系。通过计算分析可以得出，3个测试工况的危险度求和均接近实际用户危险度求和，均达到匹配模型的要求。

(2)首次建立了智能汽车测试工况有效性评价模型，评价模型定义了加速系数、危险度覆盖率、最大危险度、危险度分布相似性4个要素，综合提出了有效性指数，对测试工况的有效性进行科学定量评价。

(3)本研究建立的关联模型和有效性评价模型，为智能汽车测试工况的制定和评价奠定了理论基础，文中对模型验证数据较少、场景单一，后续研究将进一步丰富验证数据，完善“危险度”模型，更加科学合理的揭示智能汽车测试工况与用户工况的内在关系，实现用户工况到测试工况的快速科学映射。