基于社会力的自动驾驶汽车行人轨迹预测模型

杨文彦，张 希，陈 浩，金文强

(上海交通大学 机械与动力工程学院，上海 200240)

0 引言

行人是重要的交通参与者，由于缺乏外界保护，行人也是交通参与者中最为弱势的群体，除此之外，行人的运动特性与过街时的行为特征复杂多变，在人车混行的路口，面对来车，行人可能采取加速前行或止步避让等不同的行动[1]。人类驾驶员可相对容易地判断出行人的意图，进而选择继续行驶或是停车避让，而自动驾驶场景下，仅通过传感器检测、跟踪难以得出行人下一步的运动轨迹，如果只要检测到有行人就停下避让，在一些场景下可能使车辆的控制过于保守，影响通行的效率，而错误的判断则可能造成人车相撞导致行人伤亡的惨剧。研究表明，当车辆以50 km/h的速度行驶时，提前0.16 s进行制动，可使人员伤亡的概率降低15%[2]，由此可见，为自动驾驶汽车建立行人轨迹预测模型，对可能与车辆产生交互的行人的运动轨迹进行预测，能够给自动驾驶汽车的控制预留时间，提高安全性与通行效率。

国内外学者已经开展了一些行人轨迹预测的相关研究，包括基于多重环境的行人过街行为预测模型[3]；基于动态贝叶斯网络(Dynamic Bayesian Network，DBN)的概率预测模型[4];基于马尔可夫链，考虑行人个性和过去行为状态的预测模型[5]；分析行人微观动力学特性的社会力模型(Social Force Model)[6]等。社会力模型由Dirk Helbing和Peter Molnar提出，将行人与外界空间的相互作用量化为引力和斥力，此后许多学者在此基础之上对社会力模型做出了改进，例如由单个行人拓展到人群[7]，考虑行人的路径选择[8]等，并将其运用到轨道交通行人流仿真[9]、人群疏散[10]、信号灯控制下路口行人过街仿真[11]等领域。

上述研究，提出行人过街与否的概率模型，或是从微观动力学的角度研究行人的行走行为，进行模拟和仿真，鲜有预测行人行走的精确轨迹用于自动驾驶领域。基于以上问题，本研究提出一种基于社会力的自动驾驶汽车行人轨迹预测模型，整合了判断行人行为意图的行人走、停决策和改进的社会力模型，首先通过行人走、停决策判断行人面对来车选择继续行走还是停下避让，对于继续行走的行人，通过改进的社会力模型预测其行走轨迹，模型还考虑了性别、年龄等行人个体特征对其决策与轨迹的影响，模型框架如图1所示。

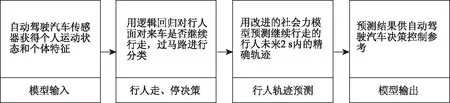
图1 模型框架Fig.1 Model framework

1 行人走、停决策

在人车混行的路口，过街的行人面对来车可能选择继续行走，也可能选择停下避让，准确地判断行人是否会继续行走，是行人轨迹预测的前提。行人是否继续行走，受到多种因素的影响，包括行人个体特征和人车之间的距离、车速。图2为本研究所考虑工况。

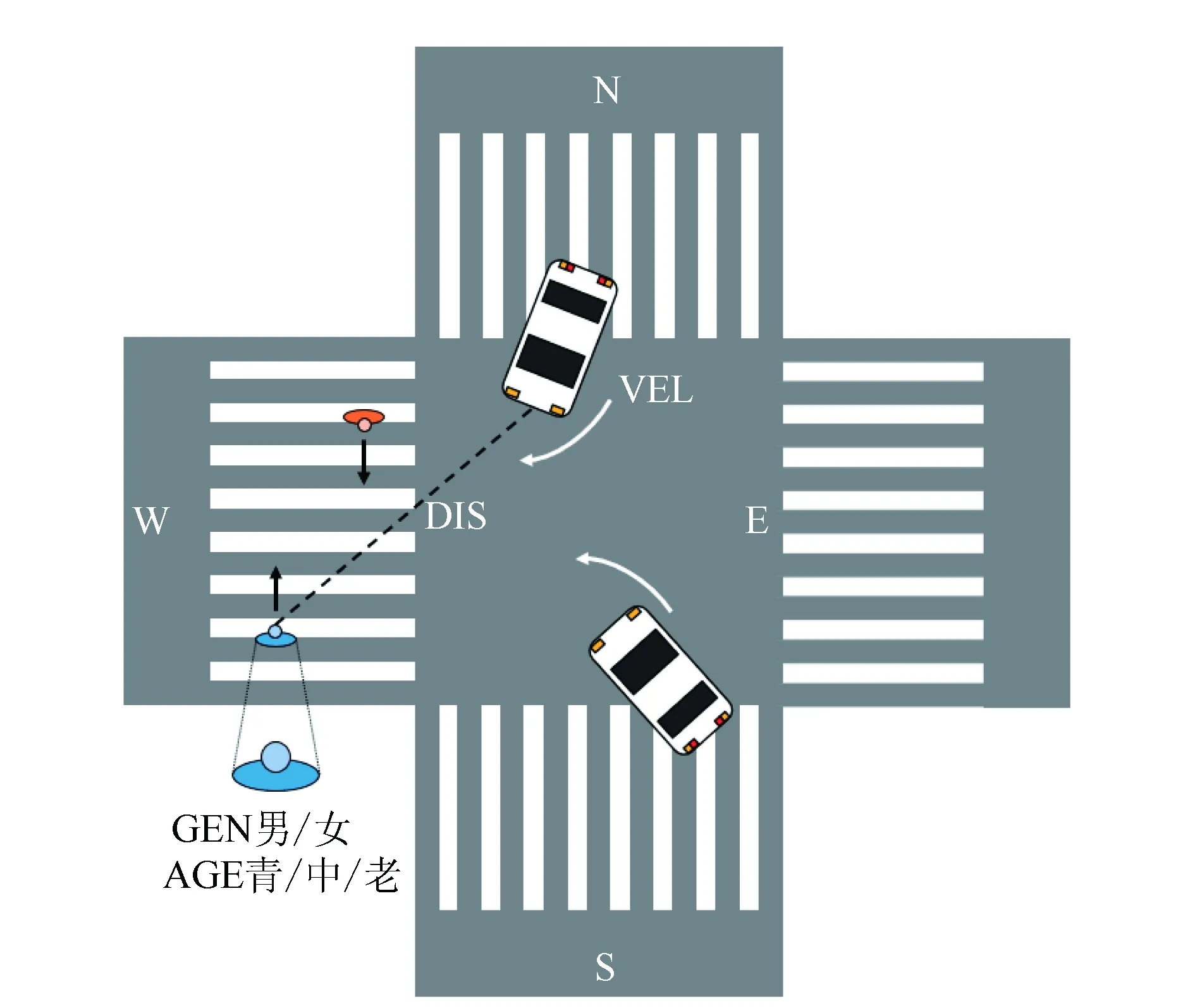
图2 行人走、停决策工况Fig.2 Working condition of pedestrian’s walking or stopping decision

考虑一十字路口，当南北方向信号灯为绿灯时，行人通过斑马线过街，南北方向行驶的车辆左转或右转进入东西方向，由此与行人产生冲突。考虑以下4个因素作为自变量:(1)行人的性别GEN,男：1;女：0。(2)年龄AGE，青年(30岁以下)：0；中年(30～60岁)：1；老年(60岁以上)：2。(3)人与车之间的距离DIS，如图2所示，定义为行人到车头中部的距离。汽车的行驶速度为VEL。行人面对来车是否继续前进(走：1，停：0)作为因变量，对行人的行走行为进行分类。行人的走、停决策基于二元逻辑回归，假设函数hλ的表达式为：

(1)

式中，自变量x=[1,GEN,AGE,DIS,VEL]T为一向量，第1项对应常数项，其余各项对应前文所述4个影响因素。λ=[λ0,λ1,λ2,λ3,λ4]T为逻辑回归的系数，通过训练得到。逻辑回归的代价函数为：

ln[1-hλ(x(i))]}，

(2)

式中，m为训练样本的数量；hλ(i)为样本i的假设值；y(i)样本i的真实值。给定初值λini，通过梯度下降的方式求得代价函数的全局最优，此时的λ就是模型所需的系数，如表1所示。

表1 逻辑回归系数Tab.1 Logistic regression coefficients

将训练好的模型用于走、停决策，将某场景下的自变量x代入公式(1),hλ>0.5时认为行人继续行走；hλ<0.5时认为行人会停下等待。

2 改进的社会力模型

2.1 模型简介

自Dirk Helbing和Peter Molnar提出社会力模型[6]后，许多研究者根据不同的应用场景提出了一系列社会力模型的变体[12-14]。在上述研究的基础上，针对人车混行路口的应用场景进行了改进，着重考虑了混行路口环境(斑马线、车辆)对行人的影响，改进的社会力模型公式为：

Fα=Fd+Fb+Fp+Fv，

(3)

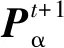
2.2 驱动力

驱动力为驱动行人向目标点移动的力，假定行人在没有干扰的情况下沿直线向目标点走去，受到其他行人和环境干扰时，行人的行走方向会发生变化，此时，驱动力Fd将使行人回到原来的行走方向上。驱动力的公式为：

(4)

式中，vd为理想速度矢量，其大小为理想速率vd；vα为实际速度矢量，通过公式(3)迭代计算得到，τα为调整时间，衡量行人速度变化的快慢。

驱动力示意图如图3所示，在实际应用中，为了确定目标点，利用自动驾驶汽车车载传感器观测行人1 s，由观测1 s内行人的起点和终点连线方向作为行人行走的理想方向，向量vd的方向即为此方向。

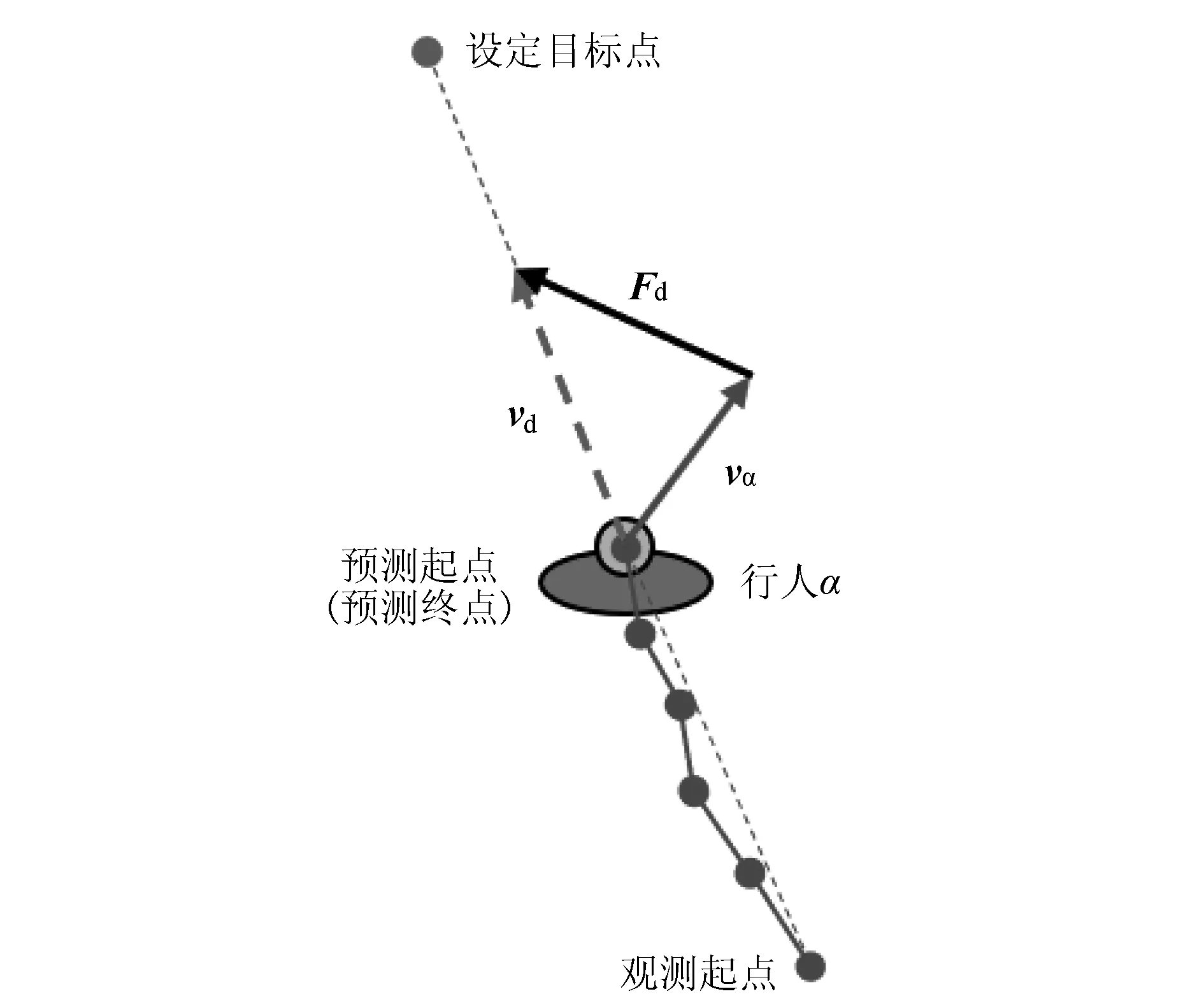
图3 驱动力Fig.3 Driving force

2.3 斑马线约束力

行人过马路时，通常会在斑马线内行走，以获得更高的安全感。模型假设当行人因避让他人或车辆等原因行走在斑马线外时，斑马线边界会有一作用力使其回到斑马线内部；当行人在线内，但因周围环境影响有走出线外的趋势时，斑马线边界对其有一作用力使其继续保持在线内行走。斑马线约束力的公式为：

(5)

2.4 行人间相互作用力

在一定范围内，行人面对迎面走来的其他人会有避让的趋势，这种趋势通过行人之间的相互作用力体现。关于这个力的作用范围，已有研究给出了结果，例如：半径10 m，圆心角120°的扇形[15]；半径8 m，圆心角170°的扇形[16]。在本研究中，斑马线总长度较短，约为8.4 m。综合考虑斑马线长度、行人的观察习惯，设定力的作用范围为半径R=6 m，圆心角Angle=170°的扇形，扇形的对称轴与行人α的速度向量vα方向在一条直线上。行人之间的相互作用力示意图见图5，为了表示得更加清晰，图中只画出了行人α的受力情况，行人β1和β2在行人α的力作用范围内，行人β3不在此范围内，因此，行人α和行人β1和β2之间存在相互作用力。经典社会力模型[6]中，行人之间排斥力的势场为一椭圆，参考经典社会力模型，通过以下方法构造此椭圆：以行人α和行人β1为例：行人β1在时间步长Δt内以速度vβ1行走了一段位移向量，以该向量的起点和终点作为椭圆的两个焦点，以行人α作为椭圆上一点构造椭圆。bβ1为椭圆的半长轴，ταβ1为椭圆上行人α所在点的切线方向，nαβ1为椭圆上行人α所在点的法线方向，行人α受到行人β1对其作用力亦沿此方向，行人α受到行人β2对其作用力同理。

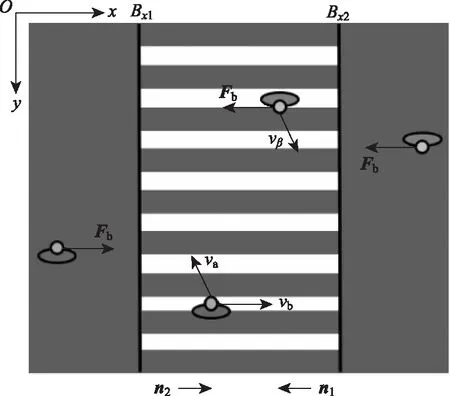
图4 斑马线约束力Fig.4 Boundary force of crosswalk

行人α受到行人β对其作用力的公式为：

(6)

图5 行人之间相互作用力Fig.5 Effect forces between pedestrians

式中，Ap为强度系数，Bp为距离系数，两者待标定；Pα和Pβ为行人α和行人β的相对于原点的位置向量；vβ为行人β的速度向量；Δt为时间步长；nαβ为图5所示力场椭圆上行人α所在点的法线方向；bβ为椭圆的半短轴。行人α受到的其他行人对其作用力的合力为：

(7)

2.5 车辆对行人影响力

面对来车选择继续行走通过马路的行人会受到车辆对其影响力，具体表现为：横坐标方向上有远离来车的运动趋势，纵坐标方向上有加速，尽快通过的趋势，其表达式为：

(8)

式中，Av为强度系数，Bv为距离系数，两者待标定；车辆对行人影响力与人车之间距离有关，此外，不同于行人与行人，行人于车辆在大小上存在差异，为了衡量这种差异，将行人和车辆等效为圆形，人的半径为rα，车辆的半径为rv，定义为车宽的一半；dαv为从车头中点指向行人的向量；ταv为垂直于dαv且远离车辆方向的单位向量。车辆对行人影响力如图6所示。

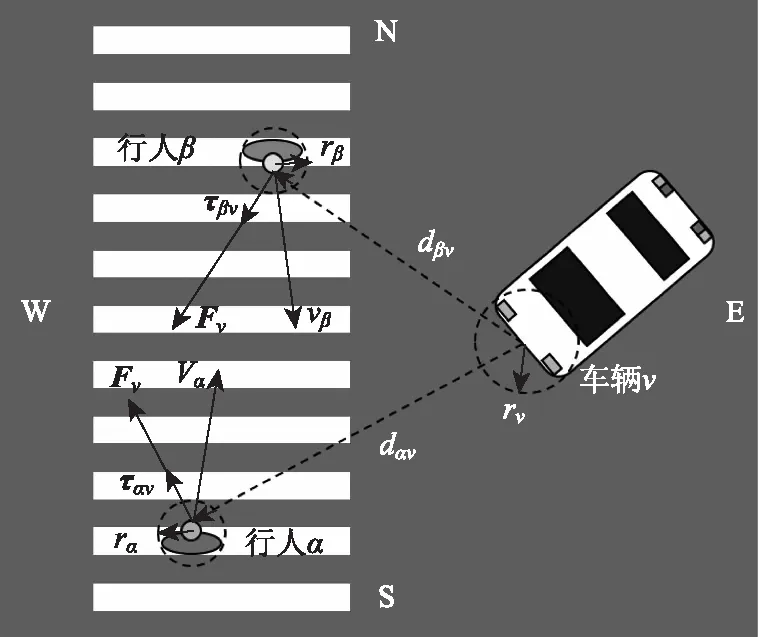
图6 车辆对行人影响力Fig.6 Influence force of vehicle on pedestrians

3 数据采集与模型参数标定

3.1 数据采集

为了标定改进社会力模型中各分力的常系数，以及验证轨迹预测的准确性，需要采集真实的行人行走轨迹。在中国上海某人车混行路口，通过四旋翼无人机，从40 m左右的高度，俯视角度拍摄行人行走的轨迹，另外，在路口两侧架设相机，同步地拍摄行人行走的视频，从中得到行人的性别和年龄，数据采集的示意图如图7所示。

图7 数据采集方法Fig.7 Data collection method

采集的行人行走数据共9 h30 min，经过筛选，共有525组行人的轨迹被运用到参数标定中，120组行人轨迹被运用到模型验证中。

3.2 坐标转换

采集的行人轨迹，通过视频处理，以0.2 s为间隔，分割为图片，使轨迹离散化，再通过图像处理，得到图片中行人的像素坐标。为了获得行人的位置、速度、加速度等运动状态信息，需要将图片中的像素坐标转化为与现实尺度对应的物理坐标。利用直接线性变换法[17-18](其示意图如图8所示)进行坐标变换需要先确定4个参考点，取斑马线4个角点，实地测量，构建物理坐标系，得到参考点的物理坐标，参考点的像素坐标通过图像处理得到，将2组坐标代入线性方程组：

(9)

式中，u=[u1,u2,u3,u4]T和v=[v1,v2,v3,v4]T为参考点像素横、纵坐标向量；x=[x1,x2,x3,x4]T和y=[y1,y2,y3,y4]T为参考点物理横、纵坐标向量；l1～l8为待求的转换系数，图片的像素坐标y方向向下为正，为了统一，建立的物理坐标系也一律取y方向向下为正。

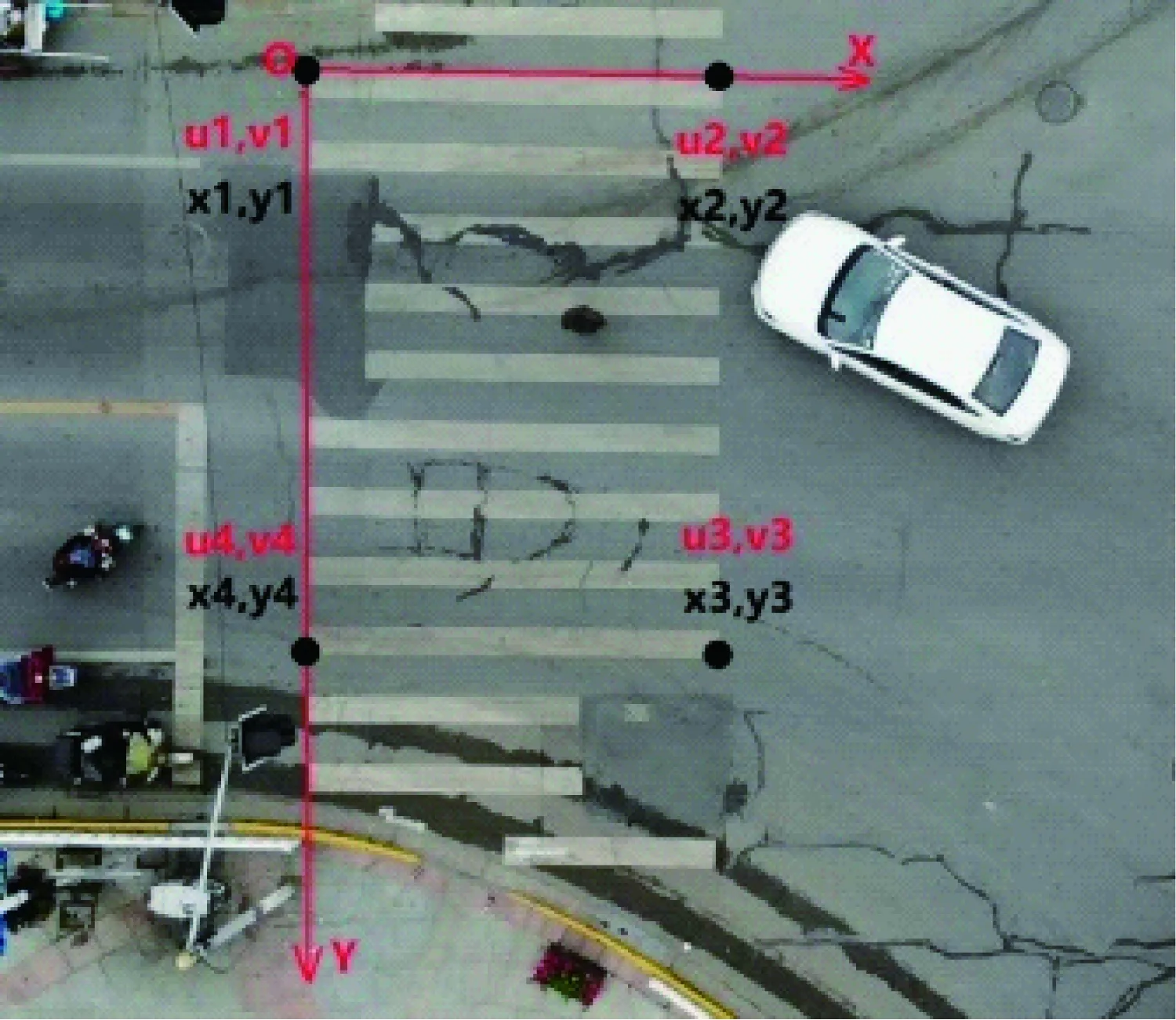
图8 直接线性变换法Fig.8 Direct linear transformation method

求解线性方程组，得到转换系数l1～l8后，对于一点的像素坐标[u,v]T，可以利用式子：

(10)

将其转换为物理坐标[x,y]T。

3.3 改进的社会力模型参数标定

本研究改进的社会力模型中的参数，一部分可以通过观察行人行走轨迹直接获得，这部分参数称为可测量参数，另一部分参数无法通过观察行走轨迹直接得到，需要用统计学的方法获得，这部分参数称为不可测量参数。

3.3.1可测量参数标定

可测量参数包括行人的理想速率vd和调整时间τ，这两个值会影响公式(4)所示驱动力Fd的大小。和走、停决策相同，将不同年龄段的行人划分为3类：青年：30岁及以下；中年：30～60岁；老年：60岁及以上。本研究的场景下，儿童大多和成年人结伴而行，其参数与同行成年人一致。

行人的理想速率vd定义为：行人在没有他人、车辆等外界因素干扰下，在斑马线内沿直线行走时速度的大小，此参数的标定通过选取符合定义的行人行走视频，通过视频处理与图像处理，图片帧之间位移差和时间差相除得到。标定结果显示，不同年龄段行人的理想速率存在一定的差异，青年人理想速率vd的均值μ=1.53 m/s，标准差σ= 0.163 m/s；中年人μ= 1.35 m/s，σ= 0.157 m/s；老年人μ= 1.21 m/s，σ= 0.150 m/s。

行人调整时间τ定义为：行人从当前速度(一般为一个较低的速度)加速到理想速度所需的时间，此参数的标定通过视频与图像处理，通过记录行人从开始行走加速到匀速行走所需的时间得到。标定结果显示，不同年龄段行人的调整时间存在一定的差距，青年人调整时间τ的均值μ= 1.60 s，标准差σ= 0.224 s；中年人μ= 1.61 s，σ= 0.288 s；老年人μ= 1.66 s，标准差σ= 0.299 s。

3.3.2不可测量参数标定

不可测量参数为改进的社会力模型各分量中的常系数，这些系数无法从图像中直接测量获得，对于这些参数，使用极大似然估计(Maximum Likelihood Estimation)法[19]进行标定。

令参数向量θ=[Ab,Bb,Abr,Bbr,Ap,Bp,Av,Bv]T,假设社会力合力F=[Fx,Fy]T满足均值向量为μ，协方差矩阵为∑F的二维正态分布，F为θ的函数，所以μ=μ(θ)也是θ的函数，列出二维正态分布的极大似然函数：

(11)

式中，aj(i)为行人j在i时刻的加速度，通过图像处理方法得到。对于整段用来进行参数标定的行人轨迹，共有N个行人，每个行人j有Mj个时刻，则整段轨迹的极大似然函数可表示为：

(12)

两边取对数，得到对数形式的极大似然函数：

[aj(i)-μ(θ)]。

(13)

求对数极大似然函数lnL(θ,M,N)对于θ的导数，令导数为0得到对数极大似然函数的最大值，此时的θ各分量的值就是参数标定的结果，不可测量参数的标定结果如表2所示。

4 模型验证

通过3.1节所述数据采集方法，3.2节所述数据

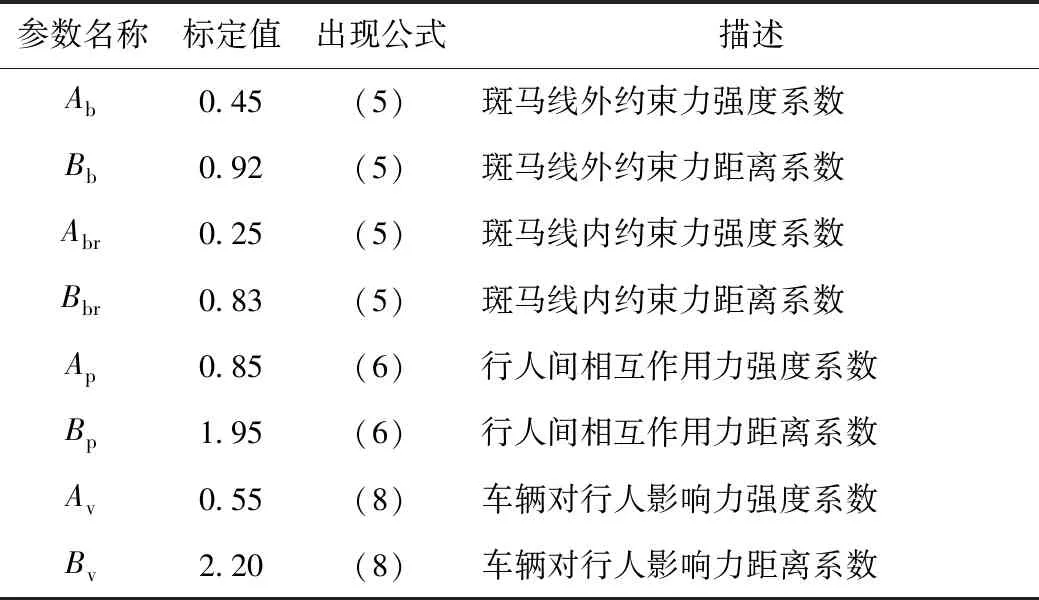
表2 不可测量参数Tab.2 Non-measurable parameters

处理方法可以得到行人面对来车所采取的真实决策和行人行走的真实轨迹，将相同的初始条件输入行人走、停决策和改进的社会力模型，可以得到模型对于行人走、停及其行走轨迹的预测结果，通过真实轨迹与预测结果的对比来验证模型的准确性。

进行验证的路口为中国上海某人车混行的路口，其中，路口的宽度为11.85 m，斑马线宽度为6.00 m，车辆接近、通过斑马线时的平均速度为3.36 m/s。

4.1 行人走、停决策验证

对于100个有过马路意向的被测行人，一方面记录他们面对来车的所采取的真实反应(继续行走、停下等待)，另一方面通过图像与数据处理，得到性别、年龄、人车距离、车速等自变量，并将自变量x=[1,GEN,AGE,DIS,VEL]T导入公式(1)所述的假设函数中，得到逻辑回归预测的结果，表3为逻辑回归分类。

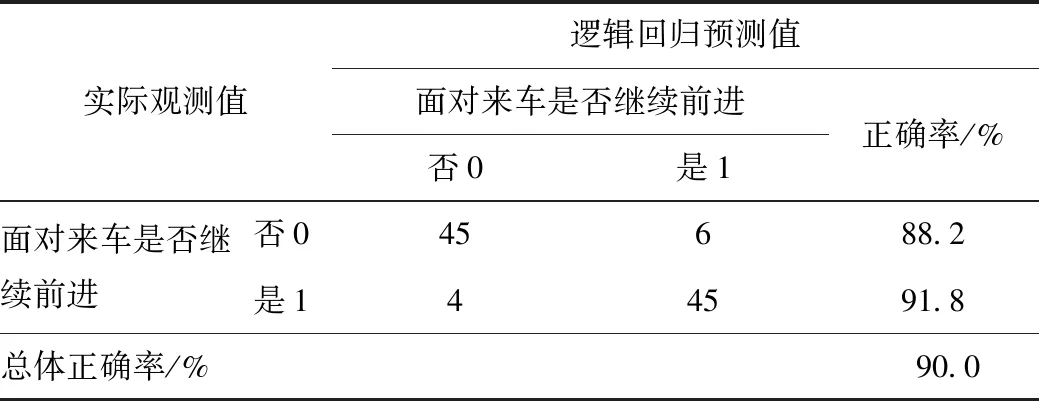
表3 逻辑回归分类Tab.3 Classification of logistic regressions

对于实际选择继续前进的行人，走、停决策预测其行走的正确率为91.8%；实际选择停下等待的行人，走、停决策预测其停下的正确率为88.2%；走、停决策总体预测正确率为90.0%，能够在一定程度上判断面对来车行人的行为，为轨迹预测做好准备。

4.2 改进的社会力模型验证

改进的社会力模型的准确程度通过行人的真实轨迹和模型所生成轨迹之间的差异来衡量，定义两个衡量指标：平均位移误差AE、最终位移误差FE，其公式分别为：

(14)

(15)

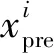
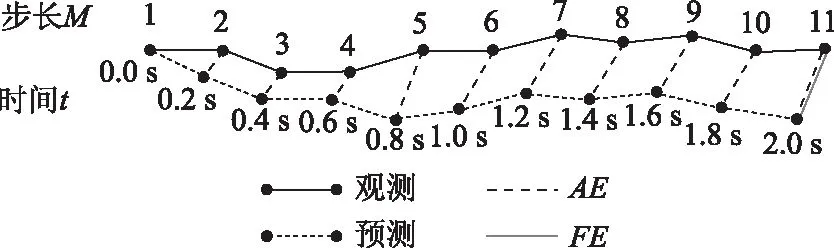
图9 误差度量Fig.9 Measurement of errors

预测的总时长为2 s，视频处理时，每0.2 s分一帧，所以整个预测过程有11帧。平均误差AE为每一帧误差的平均值，最终误差FE为最后一帧的误差。验证场景分为单个行人的轨迹预测和多个行人的轨迹预测，如图10所示。

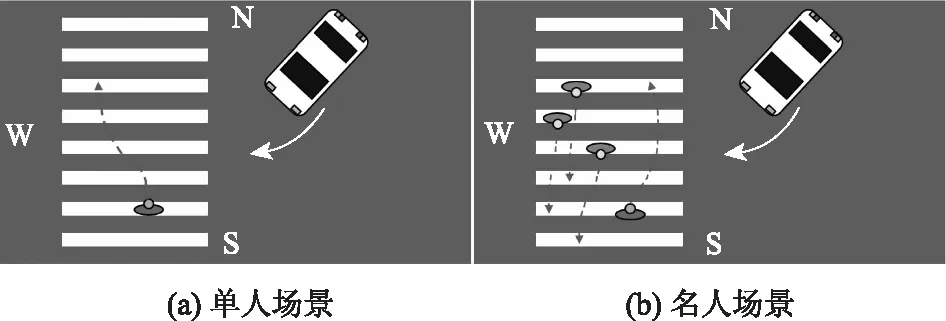
图10 轨迹预测验证场景Fig.10 Verification scenes of trajectory prediction

4.2.1单人场景轨迹预测

如图11(a)所示，某一行人自北向南通过斑马线，此时有一左转车辆与行人交互，行人在车辆影响下有向西避让的趋势，图11(b)为行人真实位移与社会力模型预测位移随时间变化的对比，图11(c)为预测轨迹与真实轨迹对比。

图11 单人场景轨迹预测Fig.11 Trajectory prediction of single-pedestrian scene

随着时间的推移，预测位移与真实位移之间的误差略有增加，但预测轨迹与真实轨迹基本重合。该场景下，轨迹预测的误差AE=0.078 m，FE=0.129 m。

4.2.2多人场景轨迹预测

图12 多人场景轨迹预测Fig.12 Trajectory prediction of multi-pedestrian scene

如图12(a)所示，5个行人(两个自北向南，3个自南向北)通过斑马线，此时有一左转车辆与行人们交互,图12(b)为5个行人位移误差的平均值随时间变化图，图12(c)为各个行人预测轨迹与真实轨迹对比图。该场景下，各行人轨迹预测误差AE的平均值为0.072 m，FE的平均值为0.145 m。

4.2.3总体验证结果

选取其他符合上述两类场景的其他真实行人轨迹各10组，取误差AE，FE的平均值，得到总体验证结果如表4所示，平均误差AE小于15 cm,最终误差FE小于25 cm，能够在一定程度上预测行人轨迹。

表4 总体验证结果Tab.4 Overall verification result

5 结论

本研究提出的基于社会力的自动驾驶汽车行人轨迹预测模型，由行人走、停决策和行人轨迹预测两大部分组成。考虑了年龄、性别等个体差异性对于行人面对来车采取决策的影响以及不同年龄行人行走速度和反应速度的快慢，并将这些差异通过改进的社会力模型予以体现。通过视频处理和图像处理完成了模型中可测量参数的标定，通过极大似然估计法完成了不可测量参数的标定。通过采集行人的真实轨迹与模型预测轨迹相对比，验证了走、停决策与轨迹预测的准确性。验证结果表明，走、停决策准确率为90.0%，轨迹预测AE的均值小于15 cm，FE的均值小于25 cm，模型具有一定的准确性。

本研究只考虑了行人轨迹的预测，然而在更为复杂的交通环境中，还存在着骑自行车(电动车)等其他交通参与者与自动驾驶汽车发生交互的情况，准确预测他们的运动轨迹，对于交通安全很有意义，这也是接下来研究方向所在。