黄土边坡悬臂式与全埋式单桩抗滑桩现场模型试验

李 哲，朱振国，张 娟，曹升亮

(1.长安大学 公路学院，陕西 西安 710054；2. 中交第一公路勘察设计研究院有限公司，陕西 西安 710075)

0 引言

抗滑桩广泛应用在公路边坡支挡设计中，按桩后土的边界条件可分为悬臂式和全埋式抗滑桩等。这种差异导致两类抗滑桩在相同的滑坡推力作用下展现出不同的受力变形过程。在这方面，国内外学者利用各类缩尺模型试验对模型抗滑桩进行了多角度的研究，分析了抗滑桩在不同边界条件下土压力分布模式和桩身内力分布状态，如Wei Dong Guo[1]等研究了模型桩(700 mm×50 mm圆形截面桩)在土体水平移动作用下的受力状态，试验中控制的变量包括水平移动的土体高度和施加在模型顶的法向荷载，其中，当法向荷载等于0时，该试验相当于模拟了全埋式抗滑桩的荷载传递过程，在此条件下得到的桩身弯矩曲线近似呈“S”形分布。刘洪佳[2]等将4根缩尺模型抗滑桩并排埋置在3.4 m×1.8 m×2.1 m的模型箱中，模拟悬臂式抗滑桩的受力状态，采用竖向堆载的方法对滑体土块施加荷载，达到模拟侧向完全临空时滑坡体与抗滑桩相互作用的效果，得出重塑黄土条件下模型抗滑桩桩侧土压力、土抗力及桩身弯矩分布规律，模型桩的破坏点位于滑面以下25 cm。祝廷尉[3]等，进行了单排嵌岩抗滑桩的室内缩尺模型试验，模型桩为小尺寸钢筋混凝土构件，滑带土材料选用直径小于4 mm的玻璃珠，滑体为现场带回的原位土，基岩层采用砌体结构，测定了嵌岩抗滑桩桩侧压力分布形式及合理作用点位置。魏作安[4]亦通过独特的方法对单排抗滑桩受力特点进行室内试验研究，推导出作用在抗滑桩上的滑坡推力表达式。文献[5-8]中均采用了不同的方法探究抗滑桩受力及失效特性，总结这些单排抗滑桩室内模型试验后发现：室内模型试验桩周土材料为重塑土，其应力应变曲线与原状土差别较大，试验研究成果反映了重塑土与桩的相互作用，但难以反映原状土条件下桩土相互作用关系。

因此， 针对黄土边坡中的单排抗滑桩提出新的缩尺模型试验方案，将前人使用的室内方法移至现场边坡平台上，以单桩形式分别研究桩顶埋设在边坡平台上和桩顶埋设在边坡坡脚的单排抗滑桩，揭示单桩条件下抗滑桩在原状黄土中的受力变形及失效规律，为黄土边坡中的单排抗滑桩设计计算提供试验支持。

1 抗滑桩原位模型试验

1.1 依托工程介绍

延西线G65w高速公路沿线存在多个人工高陡边坡，自通车以来，多个工点边坡及其内部的抗滑桩出现持续位移。沿线边坡中的抗滑桩主要分为两类，一类是桩顶埋设在边坡平台上的抗滑桩，称为半坡桩，占绝大多数，另一类是桩顶埋设在边坡坡脚处的抗滑桩，数量较少。取沿线同时包含两类抗滑桩的典型工点列于图1中。

图1 岳屯边坡剖面图Fig.1 Profile of Yuetun slope

从桩前桩后土的边界条件来看，半坡桩处于悬臂式与全埋式抗滑桩之间，因其桩前土侧向临空条件，在设计该类抗滑桩时，往往不考虑临空部分的桩前土抗力，因此将其归于悬臂式抗滑桩，坡脚桩为全埋式抗滑桩。

1.2 试验选址

高边坡上的现场模型试验选址应满足安全性、场地尺寸、运输条件等均满足要求的地点。位于延西线G65w高速公路万花隧道出口处高陡边坡，其第4级平台宽度约20 m，长度约100 m，综合比选后确定该处为现场模型试验场地。

图2 模型试验场地图Fig.2 Photo of model test site

现场土体各参数由试验前开展的大型原位直剪试验和常规室内试验综合确定，见表1。

1.3 试验相似比

现场模型试验的关键构件为模型桩，现浇法无法满足传感器安装要求，故模型桩的制作方法选用预制法。在成桩材料选择上，钢管[9]、石膏、砂混合物[10]、尼龙材料[11]、PVC管[12]等，很多研究者选用与原型相同的钢筋混凝土材料，取得了较好的试验效果[13-16]。参照文献[3]中提出的模型桩相似比设计和成桩工艺，本次现场模型试验所用模型桩的几何相似比取1∶40。相应的各物理量相似比分别为：CE=1,Cσ=1,Cε=1,Cρ=1,Cq=1∶40。其中E为弹性模量，σ为桩身应力，ε为桩身应变，ρ为桩内配筋率，q为桩侧荷载。

表1 现场土体参数Tab.1 Parameters of in-situ loess

原型抗滑桩截面尺寸为2 m×3 m，桩长25 m～40 m不等，考虑到模型桩在原状土中的嵌固问题，模型桩取最长桩长设计，即按桩长40 m的原型抗滑桩进行相似设计。原型抗滑桩中桩内配筋采用多排有效直径为64 mm的HRB400钢筋束，受拉区配筋率约为0.4%。按照相似比计算所得模型桩参数见表2所示。其中模型桩桩顶加长5 cm用于架设百分表。2.37×104N/mm2

表2 模型桩参数表Tab.2 Parameters of model pile

模型桩截面钢筋布置见图3。

图3 模型桩截面钢筋布置图(单位：mm)Fig.3 Layout of reinforcement in model pile (unit: mm)

模型桩桩身传感器包括混凝土应变片和微型土压力盒，如图4所示。

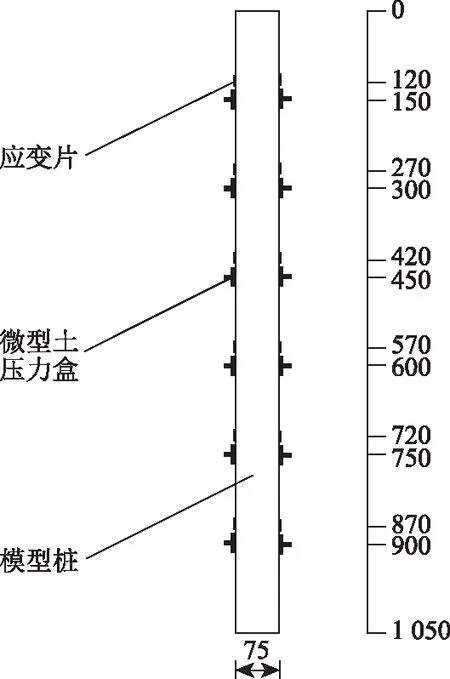
图4 模型桩桩身传感器布设图(单位：mm)Fig.4 Layout of sensors on model pile (unit: mm)

1.4 试验设计

现场抗滑桩单桩缩尺模型试验设计与实施过程中的主要控制点包括：

滑体土块部分设计：现场模型试验中，滑坡推力施加为试验加载的关键问题，为了保证原状土体与抗滑桩相互作用，滑体土块仿照土体原位剪切试验[10]中剪切土块的原理进行设计，土块尺寸为60 cm×60 cm×33 cm。为模拟滑坡体内部应力状态，在试验前对土块竖向固结，固结应力300 kPa。固结完成后拆除滑体土块前进方向的钢板，在掏槽位置填入原状黄土。

模型桩埋设：选用洛阳铲人工打孔的方式降低对周围土体的扰动，洛阳铲为自行加工的方形洛阳铲，尺寸60 mm×90 mm，略大于布满传感器的模型桩。打孔后在孔底夯实水泥土直至设计标高形成结实的孔壁，防止塌孔。孔内放入模型桩后，灌入水泥土浆液填塞模型桩与桩孔间缝隙，保证抗滑桩与桩周土的紧密贴合，提高与周围土体的摩擦力。

模型桩桩前土设计：模拟悬臂式抗滑桩采用人工切削土体的方法用削土刀将桩前土按现场实测边坡坡率(坡脚为51°)制备成高度为50 cm的边坡模型，共设两级台阶，台阶高度25 cm，宽度20 cm，平台宽度为15 cm，试验布置形式见图5；对于全埋式模型桩，桩顶清除桩前土表面杂草根系等，整平桩前长1 m、宽2 m范围内的土体，试验布置形式见图6。

图5 悬臂式单桩抗滑桩模型试验设计Fig.5 Model test design of single cantilever anti-slide single pile

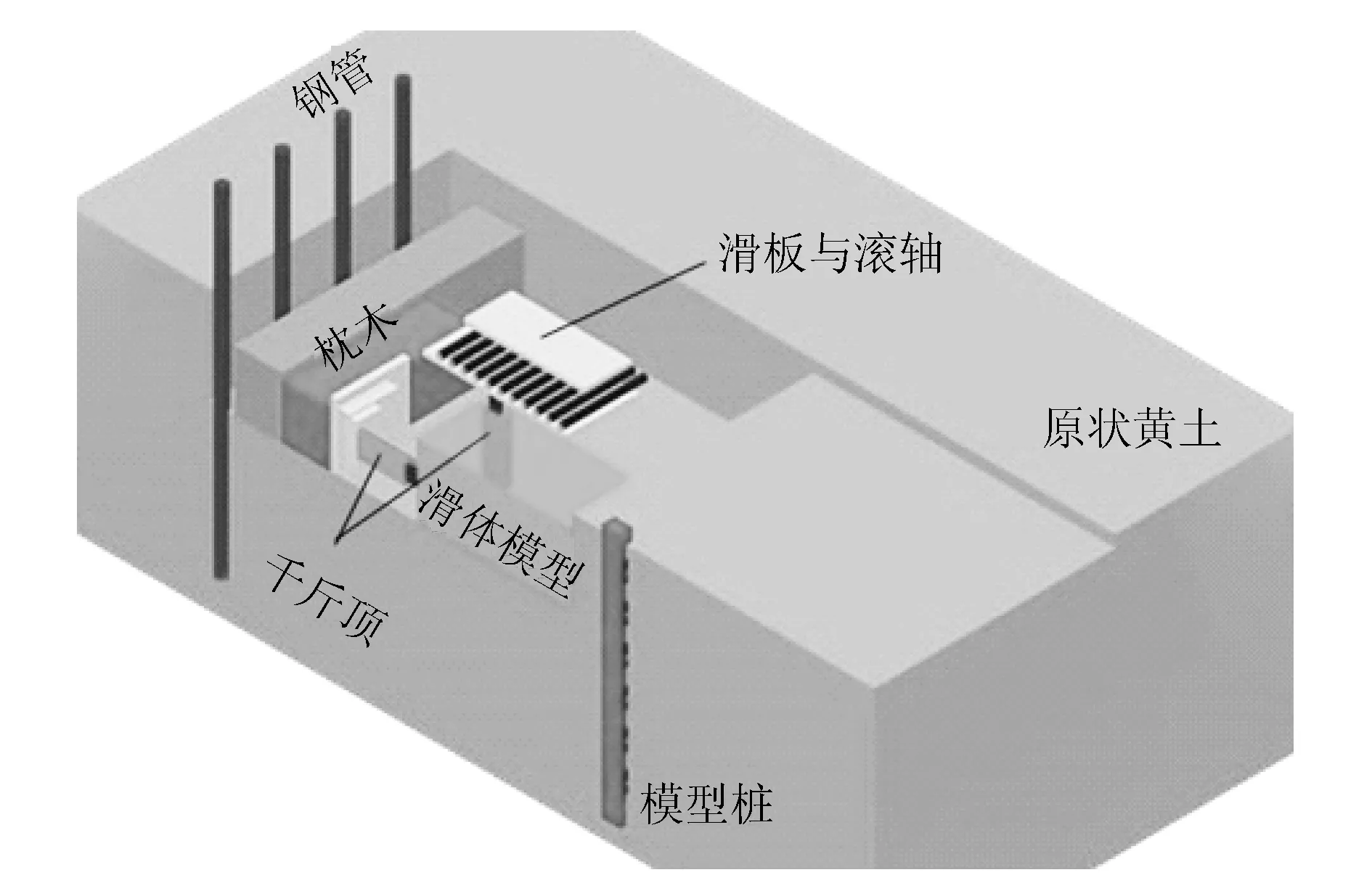
图6 全埋式单桩抗滑桩模型试验设计图Fig.6 Model test design of full-buried single anti-slide pile

1.5 模型试验水平向加载方案

试验时需要在滑体模型后侧逐级施加水平荷载，施加荷载采用液压千斤顶进行，初级水平荷载值选用法向荷载的10%，即30 kPa，后续各级荷载值为10 kPa。

水平荷载不能无限制施加，因此本次试验中，判定停止施加水平荷载的依据主要为：在同一荷载施加级数上，桩顶产生的水平向位移等于或大于滑体模型产生的水平向位移。

1.6 试验数据采集设备

试验监测数据包括滑体土块水平位移、桩顶位移、桩侧土压力及桩身应变。位移采集设备为机械式百分表，模型桩桩顶粘贴长10 cm，宽5 cm的玻璃片，扩大桩顶表面积，防止试验过程中因桩顶前进导致百分表表针滑落。传感器应变采集仪器为DH3816N静态应变测试仪，记录频率为1次/s。

1.7 试验流程

现场模型试验的主要流程如图7所示。

2 试验结果分析

2.1位移结果分析2.1.1水平和竖向位移结果分析

整理试验获得的模型桩桩顶位移数据，绘制桩顶累计位移与加载过程关系曲线，悬臂式模型桩见图8，全埋式模型桩见图9。

从图8和图9中可以看出，两类模型桩在受力变形直至破坏的过程中，模型桩桩位移以水平方向为主，在两种埋设条件下，桩顶水平位移均随荷载的增加而增长，增长的趋势由缓慢至快速。对比两种埋设条件来看，悬臂式桩桩顶出现的水平位移、竖向位移均大于全埋式桩。桩顶产生的竖向位移主要是由于桩身裂缝处以上部分发生偏转造成的，试验结束后并没有发现模型桩底部出现明显上拔趋势。

2.1.2模型桩受力阶段划分

在模型试验加载过程中，两类模型桩的水平位移值和滑体土块的水平位移值均经历了差值逐渐增大-差值峰值-差值逐渐减小的过程，当桩周土出现水平位移但其值大于抗滑桩的水平位移时，抗滑桩发挥了阻滑作用，抗滑桩到达极限状态前，桩周土的水平位移与抗滑桩的水平位移差值应为最大值，当抗滑桩的水平位移值开始接近桩周土的水平位移时，抗滑桩已经失效。因此，比较两类模型桩桩顶水平位移增量与滑体土块水平位移增量，如图10和图11所示。据此将模型桩的受力变形过程划分3个阶段：第1阶段，水平推力逐渐通过土体传递至模型桩桩身，但该阶段推力不足以使模型桩产生位移；第2阶段，在水平荷载集聚到一定程度时，桩身开始产生水平位移，但位移是在容许范围内，并未达到极限状态；第3阶段，模型桩到达极限状态，模型桩完全失效，失去其阻滑能力。

图7 试验流程图Fig.7 Flowchart of test

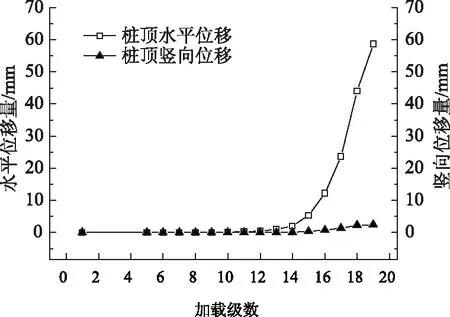
图8 悬臂式模型桩桩顶水平和竖向位移累计曲线Fig.8 Curves of horizontal and vertical displacements of cantilever model pile at pile top

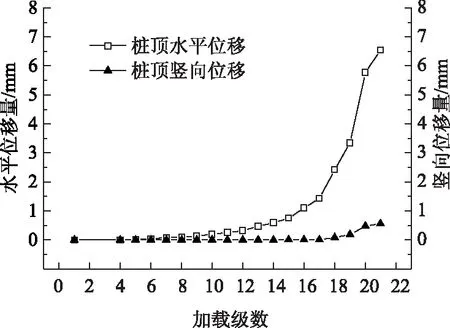
图9 全埋式模型桩桩顶水平和竖向位移累计曲线Fig.9 Curves of horizontal and vertical displacements of full-buried model pile at pile top

将3个阶段分别定义为：抗滑桩未变形阶段、抗滑桩有效变形阶段、抗滑桩失效阶段。其中3个阶段的两个界限分别定义为临界启动荷载和临界阻滑荷载。

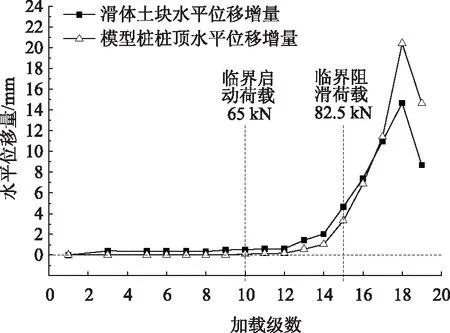
图10 悬臂式模型桩桩顶和滑体土块水平位移增量曲线Fig.10 Curves of horizontal displacement increment of cantilever model pile at pile top and landslide mass

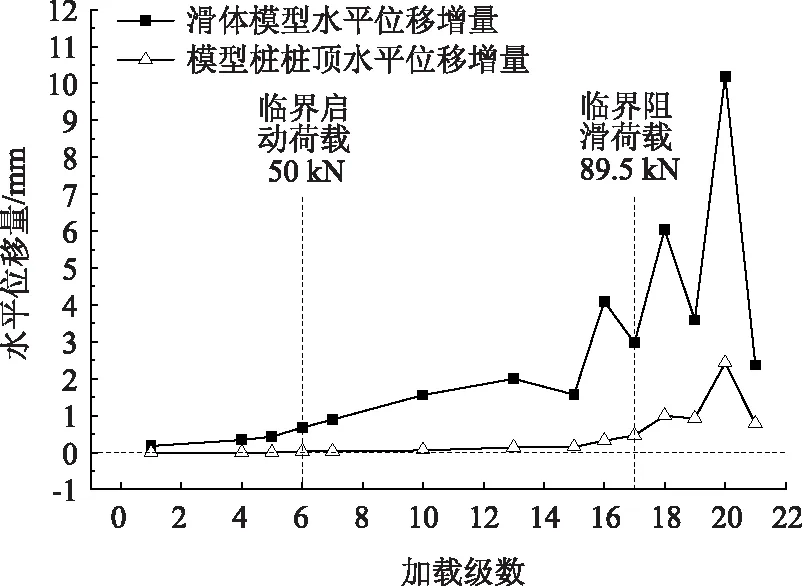
图11 全埋式模型桩桩顶与滑体土块水平位移增量曲线Fig.11 Curves of horizontal displacement increment of full-buried model pile at pile top and landslide mass

由图10可知，第10级荷载(65 kN)为悬臂式抗滑桩的临界启动荷载，第15级荷载(83 kN)为其临界阻滑荷载。由图11可知，第6级荷载(50 kN)为全埋式抗滑桩的临界启动荷载，第17级荷载(89.5 kN)为其临界阻滑荷载。

根据受力阶段划分结果对比两种埋设条件下模型桩的两个界限点发现：相比于悬臂式桩，全埋式桩的临界启动荷载较低，但全埋式桩的临界阻滑荷载明显高于悬臂式桩。因此可以确定，全埋式桩受力过程比悬臂式桩要长，且它能发挥的最大抗滑能力比悬臂式桩大。

2.2 土压力结果分析

为研究悬臂式和全埋式抗滑桩桩前土压力、桩后土抗力的变化规律及分布形式，对试验测得的微型土压力盒数据进行分析。

2.2.1悬臂式模型桩土压力分析

悬臂式单桩模型试验加载过程中模型桩桩侧各点土压力及土抗力曲线如图12所示。

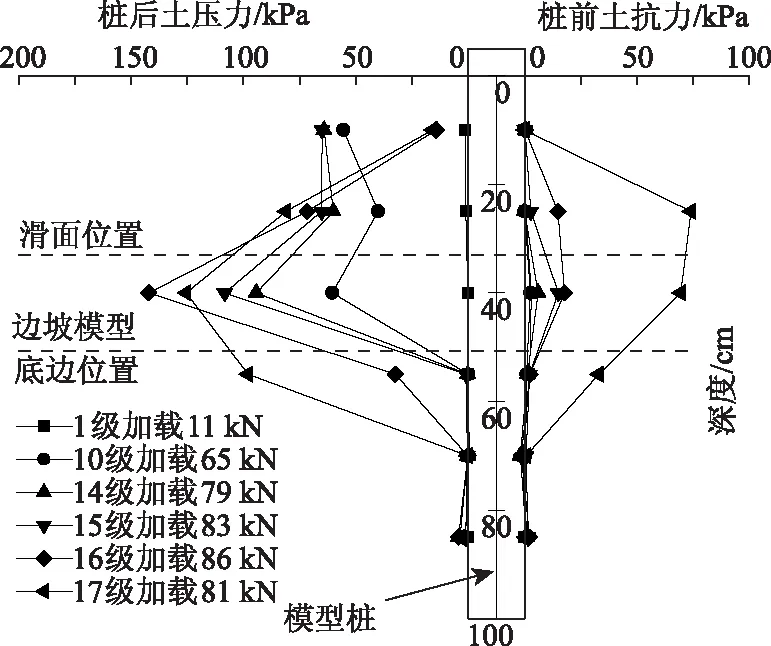
图12 悬臂式单桩模型桩侧压力变化曲线Fig.12 Curves of soil pressure on side of single cantilever model pile

悬臂式模型桩受力的前两个阶段为水平荷载传递至模型桩身使其产生弹性变形的过程，在这两个阶段中，模型桩结构完整，桩身受到的土压力随水平荷载的增加而增加，由图12可以看出，施加水平荷载过程中(1～15级)，桩身土压力分布规律近似，模型桩上部(深度0 ～55 cm范围)各个土压力盒测得的数据随着荷载的增大按分布规律逐渐增加，但在此过程中，桩前土抗力很小，很多压力盒没有测到土压力值，仅在深度40 cm处测得值较小的土压力。自16级荷载施加后，模型桩桩侧土压力和土抗力的分布形式发生明显的改变，桩前土抗力大幅度增加，说明此时桩已进入第3受力阶段，桩身已经开裂破坏。

2.2.2全埋式模型桩土压力分析

全埋式单桩模型试验加载过程中模型桩桩侧土压力及土抗力变化规律曲线如图13所示。

图13 全埋式单桩模型桩桩侧压力变化曲线Fig.13 Curves of soil pressure on side of single full-buried model pile

全埋式模型桩受力的前两个阶段亦为水平荷载传递至模型桩身使其产生弹性变形的过程，在这两个阶段中，模型桩结构完整，桩身受到的土压力随水平荷载的增加而增加，由图13可以看出，施加水平荷载过程中(1级～17级)，桩身土压力分布规律近似，模型桩上部(深度0～55 cm范围)各个土压力盒测得的数据随着荷载的增大按分布规律逐渐增加，与悬臂式桩不同的是，在这一阶段，全埋式桩出现了明显的桩前土抗力，其分布形式近似倒梯形。自18级荷载施加后，模型桩桩侧土压力和土抗力的分布形式发生明显的改变，其中桩前土抗力的分布形式变化最大，由倒梯形分布变成了随深度增加先增大后减小的分布规律，说明此时桩已进入第3受力阶段，桩身已经开裂破坏。

2.3 弯矩结果分析

试验过程中，通过对粘贴在模型桩表面应变片的连续测试，根据式(1) 进行弯矩计算。

M=EIΔε/B,

(1)

式中,M为模型桩桩身弯矩值；E为模型桩桩身材料的弹性模量;I为模型桩的截面惯性矩；B为模型桩桩身受力区应变片与受压区应变片的距离。根据式(1)分别对悬臂式和全埋式模型桩桩身弯矩进行分析。

2.3.1悬臂式模型桩弯矩分析

悬臂式单桩模型试验加载过程中模型桩桩身弯矩变化规律曲线见图14。

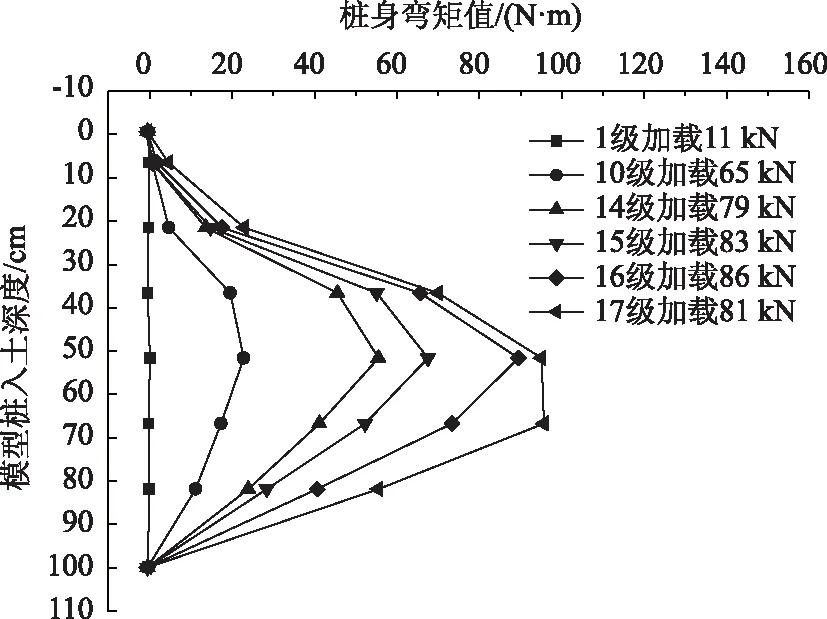
图14 悬臂式单桩模型桩桩身弯矩变化曲线Fig.14 Curves of bending moment of single cantilever model pile

由图14可以看出，悬臂式桩在水平向荷载作用下，桩身弯矩呈“D”形分布，在加载的过程中，各点弯矩值按“D”形分布规律较为均匀的增加，在深度约52 cm处，存在一个最大值点，说明悬臂式桩的最大弯矩值点在该点附近。在15级荷载施加后，桩身弯矩仍遵循原有的分布规律，但16级荷载施加后，桩身弯矩在原有分布形式下扩大了增幅，尤其是位于最大弯矩值点附近。17级荷载施加后，桩身弯矩发生重分布，最大弯矩值点下移值深度66 cm 附近，且该级荷载无法到达设计荷载(89.5 kN)。由此可以说明，模型桩的破坏是自15级加载后产生的。

2.3.2全埋式模型桩弯矩分析

全埋式单桩模型试验加载过程中模型桩桩身弯矩变化规律曲线见图15。

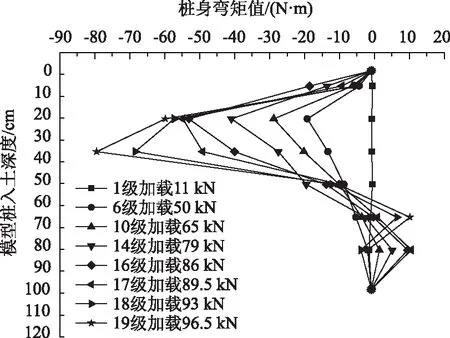
图15 全埋式单桩模型桩桩身弯矩图Fig.15 Curves of bending moment of single full-buried model pile

由图15可以看出，全埋式桩和悬臂式桩的桩身弯矩分布形态截然不同，近似呈“S”形分布，各测点的弯矩值随着水平荷载的增大均匀增减，最大弯矩值点位于深度22 cm附近。自17级荷载施加完成后，模型桩桩身弯矩开始出现小范围变化，18级荷载施加后，桩身弯矩发 生明显的重分布，反弯点上升，模型桩入土深度37 cm处测点的弯矩值成为最大弯矩值点。

2.4 破坏模式

在两类模型试验结束后，分别开挖桩周单侧土体，观察桩身破坏点位置，见图16。而后将模型桩取出，描绘其破坏形态，见图17。

图16 模型桩破坏形态图Fig.16 Failure of model piles

图17 模型桩破坏模式简图(单位:cm)Fig.17 Failure pattern of model piles(unit:cm)

悬臂式模型桩破坏点位于模型桩入土深度约67 cm 处，桩身混凝土开裂，可见内部配筋。桩前土体出现裂缝，模型桩属于单点弯折破坏，弯折方向为滑坡推力方向。

全埋式模型桩破坏点位于模型桩入土深度约32 cm 和56.5 cm处，两处破坏点开裂方向相反，其中56.5 cm处桩身混凝土开裂程度大于32 cm处，桩周土体有隆起的现象。

3 结论

(1)试验中，悬臂式模型桩在入土深度67 cm处发生破坏，该点为滑面下约35 cm处；全埋式模型桩在入土深度32 cm和56.5 cm处发生破坏，两破坏点开裂方向相反，两破坏点分别位于滑面处和滑面下约24.5 cm处。

(2)按模型试验过程中模型桩和滑体土块水平位移结果将模型桩划分为3个受力阶段，分别为抗滑桩未变形阶段、抗滑桩有效变形阶段、抗滑桩失效阶段。悬臂式模型桩对应的3 个阶段分别为加载的第1～10级、第10～15级、第15级以后，全埋式模型桩对应的3个阶段分别为加载的第1～6级、第6～17级、第17级以后。

(3)将3个阶段的两个界限分别定义为临界启动荷载：悬臂式模型桩为第10级荷载(65 kN)，全埋式模型桩未第6级荷载(50 kN)和临界阻滑荷载：悬臂式模型桩为第15级荷载(83 kN)，全埋式模型桩为第17级荷载(89 kN)。

(4)悬臂式模型桩桩后土压力值在前两个阶段与全埋式模型桩近似，两者分布曲线形态相近，但在到达第3阶段时，悬臂式模型桩土压力值几乎重分布，而全埋式模型桩土压力值分布规律与前两个阶段类似，在数值上增长快速。悬臂式模型桩出现桩前土抗力主要是在第3阶段，而全埋式模型桩在3个阶段中均出现了桩前土抗力。

(5)试验中，悬臂式模型桩桩身弯矩分布形式呈近似“D”形；全埋式模型桩桩身弯矩分布形式呈近似“S”形，桩身存在负弯矩和正弯矩并具有反弯点。两类模型桩桩身弯矩均在第3阶段时发生重分布现象。

(6)悬臂式模型桩处于第1阶段的时间较长，第2阶段很短，其受力变形破坏的时间短，破坏前桩前土抗力几乎没有出现；全埋式模型桩处于第1阶段的时间较短，第2阶段较长，其受力变形直至破坏的时间长，破坏前已经出现土抗力，使得全埋式模型桩极限抗滑能力更大。