车桥耦合振动的桥面非平稳随机激励模拟

陈水生，赵 辉，，夏钰桓

(1.华东交通大学，江西 南昌 330013；2.湖北恒大建设工程有限公司，湖北 武穴 435400)

0 引言

车辆在桥上行驶时，高低不平的桥面状况不仅影响车辆行驶安全和乘坐舒适性，也是桥梁产生随机振动的主要激励源。在空间上处于车轮与桥梁间的桥面高低起伏状况具有很大的随机性，如何建立有效的﹑贴近实际的桥面不平顺随机激励输入模型，对研究车桥耦合系统的振动规律至关重要。文献[1-2]研究桥面不平度对简支梁桥振动响应的影响；文献[3-4]用不同的方法模拟桥面不平度，分析连续梁桥的振动响应；文献[5-6]分析了桥面不平度对钢管混凝土拱桥振动响应的影响；文献[7]考虑车辆六轮的相互关系，分析不同桥面路况等级和不平顺随机激励相干程度对连续箱梁桥振动响应的影响；文献[8]研究路面平稳激励对二分之一车悬架系统振动响应的影响。上述研究的桥面不平度激励样本都是平稳的高斯随机过程，车辆在桥上是匀速行驶的。然而，当车辆变速行驶时，桥面不平度激励在时域上就是一个非平稳随机过程，此情况下采用平稳随机过程模拟桥面不平度就难以体现车桥耦合系统的非平稳振动响应特征。因此，对于由桥面不平度引起的车桥耦合振动响应研究，桥面激励应考虑为非平稳随机过程，更符合真实的车桥实际关系状态。文献[9-11]分析车辆在桥上紧急制动产生的桥面非平稳随机激励对桥梁振动响应的影响；文献[12-13]研究了路面凸凹这一非平稳路况对结构及车辆振动响应的影响;文献[14]研究四分之一车在路面非平稳激励作用下的振动响应；文献[15]分析了两轴二分之一车非匀速行驶时车桥系统的振动响应，非平稳桥面激励样本验证不充分；文献[16]基于虚拟激励法研究了桥面非平稳随机激励对桥梁振动响应的影响，但桥面不平度激励为一致激励，没有考虑前后车轮的时间滞后；文献[17-18]建立了车辆各轮相关的路面非平稳随机激励模型，但模型没有验证。针对上述研究中存在的不足，本研究建立了车辆六轮相关的桥面非平稳随机激励模型，通过工程实例验证了非平稳随机激励模型的有效性，并将非平稳随机激励应用到车桥耦合系统的振动响应研究中。

1 单轮桥面非平稳随机激励模型

设三轴汽车最前方两车轮的桥面不平顺激励为q1(t)和q2(t)，中间轴两车轮的桥面随机激励为q3(t)和q4(t)，第三轴两车轮所受的桥面激励为q5(t)和q6(t)，前轴到中轴之间的距离为l1，前轴到后轴之间的距离为l2，车辆左轮迹与右轮迹的间距为B，汽车各轮间的平面位置如图1所示。

图1 车辆六轮平面布置图Fig.1 Plane layout of 6 wheels of vehicle

以车辆行驶的距离s为变量，根据滤波白噪声法可得单轮桥面不平度为：

(1)

式中，Ωc=2πnc，nc为路面空间截止频率。由于

(2)

公式(2)代入公式(1)可得：

(3)

因为W(s)是参数化白噪声，不能直接在公式(3)中应用，依据协方差等效法可得单轮桥面非平稳随机激励输入方程[19]：

(4)

在式(4)中因为W1(t)为平稳过程，可以直接使用。

2 左右轮相关桥面非平稳随机激励模型

车辆左右轮迹的桥面激励相关模型需要输入左右轮的相干函数，在此采用文献[20]的相干函数模型。依据随机振动的理论，振动系统的输入激励与输出响应之间的互功率谱Sxy(w)为振动系统频响函数Hxy(w)与输入激励自谱密度Sx(w)的乘积，系统频响函数的模与相干函数相等，即：

|Hxy(w)|=cohxy(w)。

(5)

采用二阶Pade近似计算，将公式(5)转换为左前轮及右前轮桥面激励输入的状态方程和输出方程：

(6)

3 前后轮相关桥面非平稳随机激励模型

同一侧的轮迹，中轮和后轮的桥面激励滞后前轮一段时间，在车辆行驶速度为v时，左侧中轮和左侧后轮的桥面激励输入可写成：

(7)

根据前后轮的传递函数关系，采用二阶Pade近似计算即可求出左前轮和左中轮桥面输入相关性的状态方程和输出方程[21]：

(8)

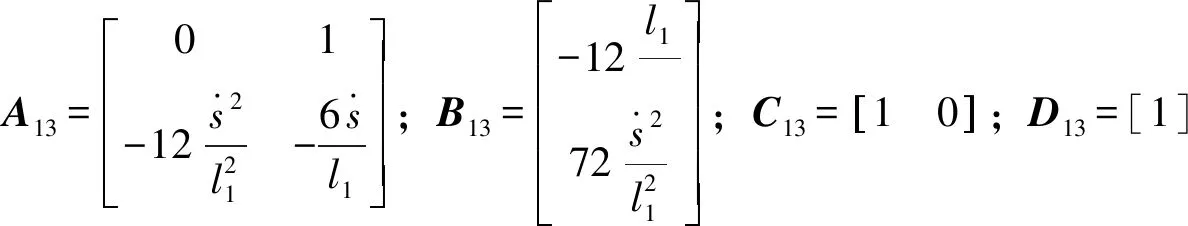
同理可得q5(t)的桥面非平稳随机激励输入的状态方程和输出方程。综上所述，便可得到车辆六轮桥面非平稳随机激励输入的时域方程为：

(9)

式中，

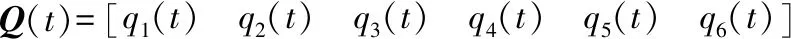
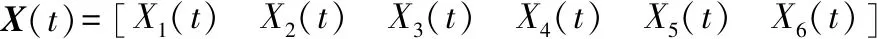
4 工程实例分析

以大塅水库桥为研究对象，该桥位于江西奉铜高速公路铜鼓县大塅镇，为3×30 m预应力混凝土先简支后连续T梁桥，单幅桥的横桥向由6片T梁组成，T梁的高度为2 m，桥梁总跨径为90 m。桥梁横断面布置：0.5 m(防撞栏)+11.65 m(行车道)+0.5 m(防撞栏)+0.35 m(隔离带)。桥面结构层分别为：4 cm厚改性沥青混凝土抗滑表层、6 cm 厚中粒式改性沥青混凝土、三层改性防水层和10 cm厚C50混凝土桥面铺装层。桥梁设计荷载为公路-I级，下部结构为桩柱式桥墩。

4.1 车辆六轮相关桥面非平稳随机激励模型验证

为了更精确地计算桥面不平度对车桥耦合系统的影响，采用LXBP-5型公路连续式八轮平整度仪对大塅水库桥的桥面状况进行了测试。在桥梁的两个行车方向上采集多组数据，其中一组桥面不平度离散数据如图2所示，利用快速傅里叶变换技术对数据进行处理可得相应的功率谱密度，实测桥面不平度的功率谱密度与国家标准GB 7031—86的比较如图3所示，从图可知，桥面状况处于B级到C级之间，在此取桥面不平度系数Sq(n0)≈128×10-6m2/m-1。

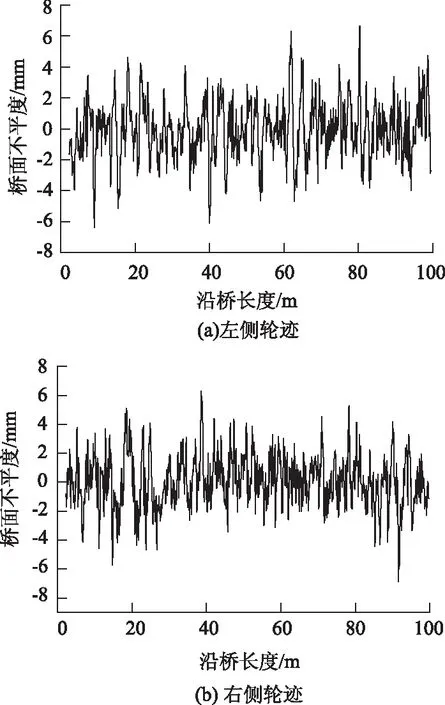
图2 实测桥面不平度Fig.2 Measured bridge deck roughness

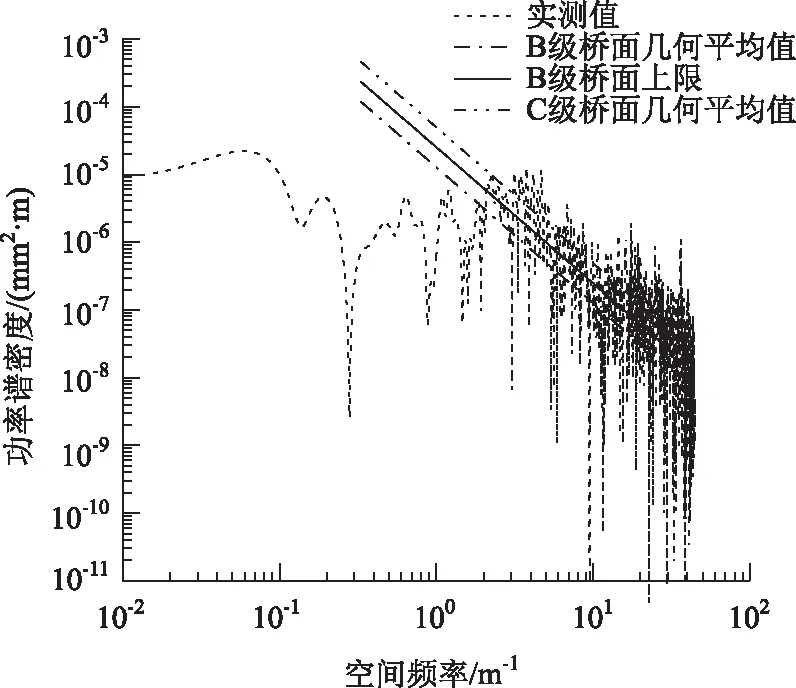
图3 实测值与国家标准对比Fig.3 Comparison between measured value and national standard values

以一辆三轴后八轮汽车为研究对象，车辆左右轮距B=1.8 m，前中轴距l1=3.6 m，前后轴距l2=4.8 m，采用大塅水库桥桥面不平度系数，按照上述方法生成桥面非平稳随机激励样本。车辆行驶的初速度v0=0 m/s，加速度a=2 m/s2，采样时间10 s,可得车辆6个车轮的桥面非平稳随机激励输入如图4所示，从图可以看出，当车辆加速行驶时，因桥面不平顺引起的非平稳随机激励信号的幅值随时间 (速度)的增大而增大。

当车辆以速度v行驶在桥梁上时，依据空间频率n和时间频率f之间的关系f=vn，可将空间频率(n1,n2)内的位移功率谱密度Sq(n)变换为时间频率(f1,f2)内的位移功率谱密度Sq(f)：

(10)

式中，空间参考频率为n0=0.1 m-1；桥面不平度系数为Sq(n0)。

对车辆各轮的桥面非平稳随机激励样本进行功率谱变换，并与公式(10)计算的理论值进行对比，如图5所示，从图中可以看出：非平稳激励样本的功率谱与理论功率谱吻合得很好。

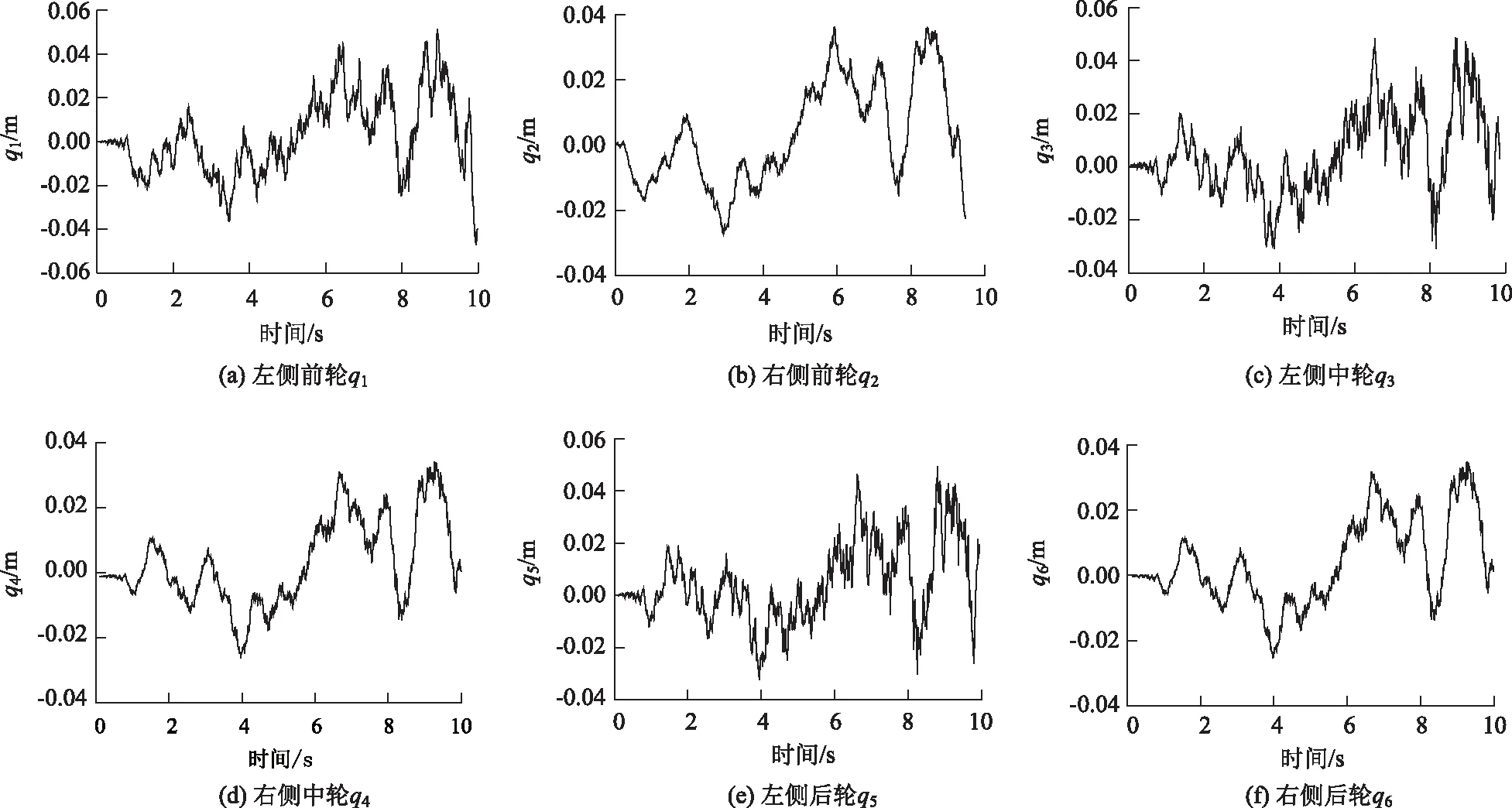
图4 六轮相关桥面输入时间历程Fig.4 Time history of 6-wheel correlated bridge deck input

图5 六轮相关桥面非平稳激励的功率谱Fig.5 Power spectra of 6-wheel correlated bridge deck non-stationary excitation

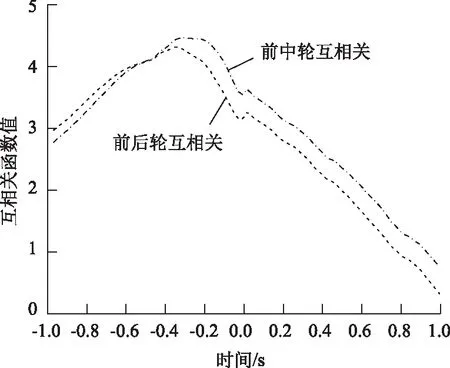
图6 前中后轮互相关函数Fig.6 Cross-correlation functions of front, middle and rear wheels

图7 左右轮相干函数值与理论值对比Fig.7 Comparison of left and right wheels coherence function value with theoretical value

4.2车桥耦合振动响应分析4.2.1车桥耦合振动方程

取车辆总重约330 kN，前轴重64.7 kN，中后轴重265.3 kN，采用传统的弹簧-质量-阻尼振动体系，将三轴汽车简化为九自由度空间模型，考虑车体竖向位移、纵向点头和侧翻，简化车辆模型如图8所示，车辆各项参数的取值与文献[16]相同。依据车辆系统振动原理，建立九自由度空间车辆振动方程如下：

(11)

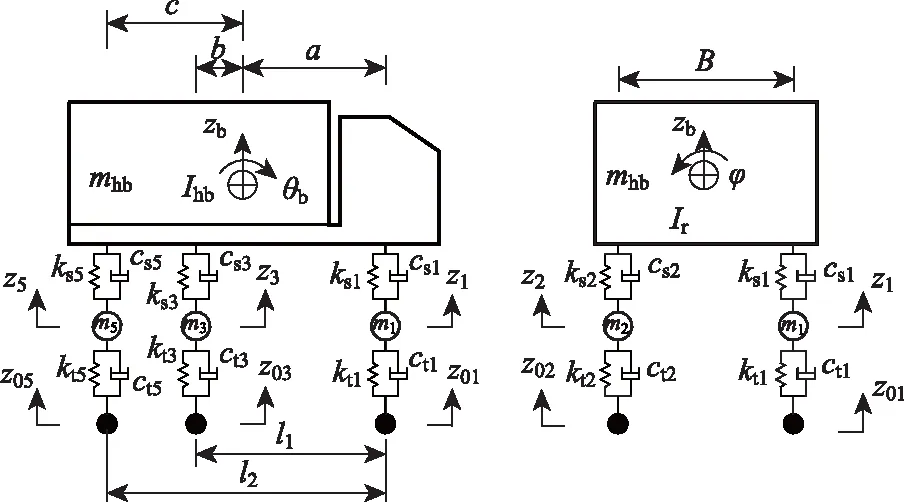
图8 车辆模型的侧面和正面Fig.8 Side and front of vehicle model

依据设计图纸的尺寸和材料属性，运用ANSYS软件建立大塅水库桥的精细有限元模型，基于对大塅水库桥现场模态测试数据，通过改变主梁、桥面铺装层和横隔梁的混凝土弹性模量及密度，使桥梁有限元模型的基频和振型特征接近现场实测数据，修正后的有限元模型如图9所示。为减少车桥耦合计算矩阵维数，采用模态综合叠加技术建立桥梁的振动方程：

(12)

(13)

式中，qi为第i个车轮的桥面不平度随机激励值，联立公式(11)～(13)，可得车桥耦合振动方程：

(14)

(15)

公式(14)中的Mbv，Cbv，Kbv分别为车桥相互作用模型的质量、阻尼和刚度矩阵；Fw为路面不平顺随机激励引起的车桥耦合竖向荷载；u为广义坐标向量，u=[y1y2…yrz1…z6zbθbφ]T。将前文模拟得到的六个车轮非平稳随机激励样本q1，q2，q3，q4，q5，q6输入到公式(15)，通过编制基于Newmark-β算法的Matlab程序求解车桥系统的振动响应。

图9 大塅水库桥有限元模型Fig.9 FE model for Daduan reservoir bridge

4.2.2桥面非平稳随机激励作用效应

当车辆在桥上加速或减速行驶时，相应的桥面不平顺随机激励为一非平稳随机过程[15,17]，其不平度的均方根值是时变的；当车辆匀速行驶，即加速度为零时，相应的桥面不平顺随机激励为一平稳随机过程[19]，其均方根值为常数，因此平稳激励是非平稳激励的特例，即加速度为零。

(1)确定性桥面不平顺激励

本研究只考虑一种荷载布置方式，即车辆正常行车道位置行驶，距离防撞栏1.475 m。按照该桥桥面不平度状况生成一组确定性桥面平稳和非平稳随机激励样本，图10给出了车辆以初始速度40 km/h，加速度为2 m/s2通过桥梁时，第二跨边梁跨中竖向振动和车体竖向振动的时程曲线，由图可得，桥梁和车辆在桥面非平稳随机激励作用下的振动响应大于平稳激励所产生的振动响应，且曲线波动大于平稳激励，其中桥梁响应曲线的峰值因车辆加速运动而相对滞后。

图10 桥梁和车辆的振动响应Fig.10 Vibration responses of bridge and vehicle

(2)随机性桥面不平顺激励

伴随着对车桥耦合振动随机激励源的研究和认识的不断深入，确定性桥面不平顺激励已不能充分体现桥面激励的随机性特征，这就有必要考虑桥面不平度激励的随机性，并进一步应用随机振动理论对桥面不平度随机激励下的车桥耦合振动响应进行统计分析。因此，本研究在分析桥面非平稳随机激励对车桥振动响应的影响时，采用蒙特卡罗法对5 000 个桥面非平稳随机激励样本进行统计，计算车桥耦合振动响应的均值和标准差。

图11为车辆以初始速度40 km/h，加速度为2 m/s2通过桥梁时，第二跨边梁跨中竖向振动位移和车体竖向振动位移的均值，从图中可以看出：平稳激励与非平稳激励的桥梁竖向振动位移均值基本重合，也充分说明桥梁的振动响应主要还是由车辆重力这一确定性荷载激励引起，桥面非平稳激励对桥梁振动响应的均值影响很小。但是，车辆振动对桥面随机激励很敏感，平稳激励作用的车体振动响应均值范围在-2～0.36 mm，而非平稳激励作用的车体振动响应均值范围在-2.58～0.86 mm，显然非平稳激励增大了车体振动响应。

图11 桥梁和车辆振动响应均值Fig.11 Mean values of bridge and vehicle vibration response

车辆以初始速度40 km/h，加速度2 m/s2过桥时的第二跨边梁跨中竖向位移响应标准差和车体上下振动响应的标准差如图12所示，桥梁在非平稳随机激励作用下的振动响应标准差明显大于平稳激励作用，可见非平稳激励的离散性较大且对桥梁振动响应标准差的影响也较大。同时，非平稳激励下的车辆振动响应加剧，响应的标准差随着车辆的行进而增大，而平稳激励作用时的车辆振动响应离散性较小，响应标准差变化不大。

图12 桥梁和车辆振动响应标准差Fig.12 Standard deviations of bridge and vehicle vibration response

当车辆以相同的初速度40 km/h，不同的加速度2，4，6，8 m/s2通过桥梁时，第二跨边梁跨中竖向振动位移和车体竖向振动位移的标准差曲线如图13所示，由图可知，桥梁和车辆的振动响应标准差随着车辆加速度的提高而增大，因为加速度的变化，引起桥面非平稳激励的幅值和频率变化，进而影响车桥耦合系统的振动响应。

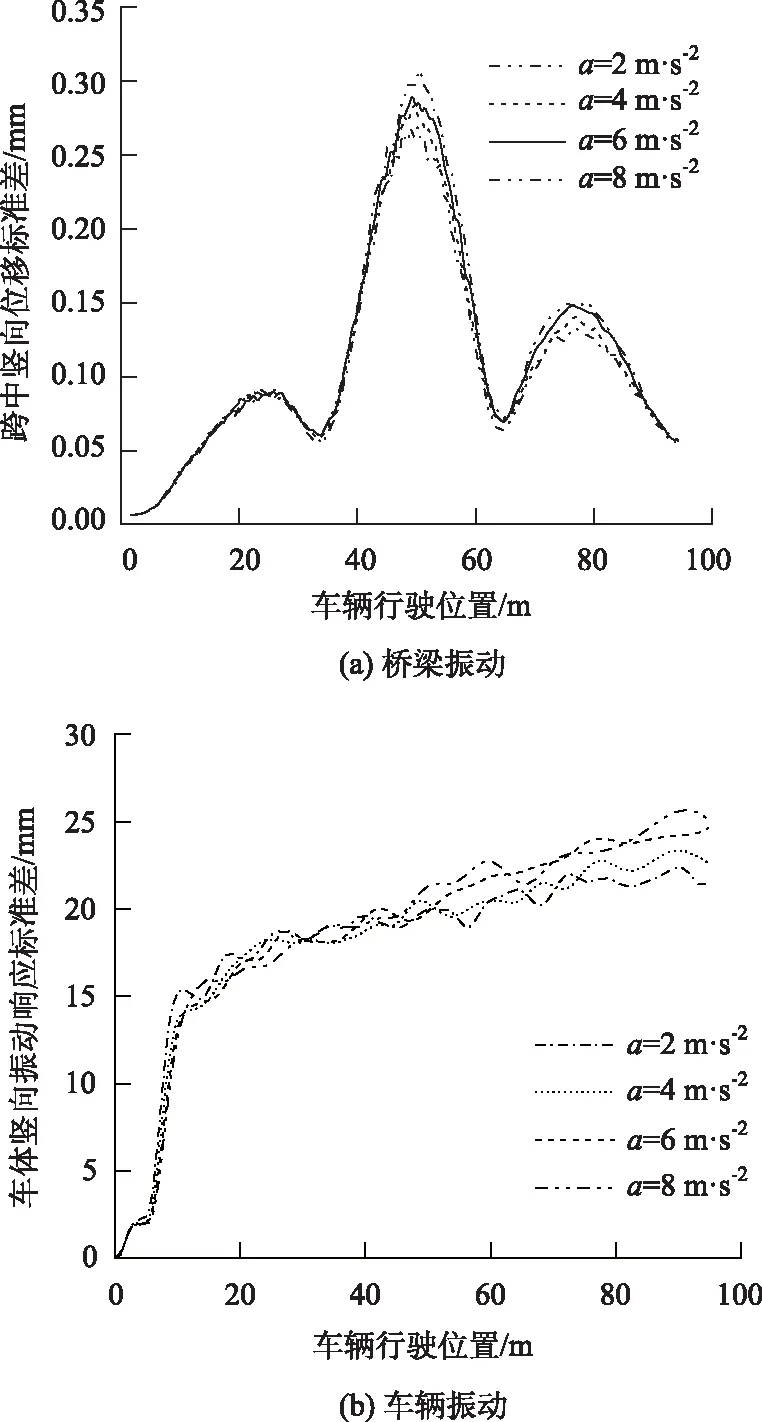
图13 不同行车加速度的桥梁和车辆振动响应标准差Fig.13 Standard deviations of vibration responses of bridge and vehicle under different accelerations

总之，桥梁和车辆的振动响应对桥面随机激励很敏感，尤其是非平稳激励作用增大了桥梁和车辆的振动响应，对桥梁运营安全和使用寿命不利，也影响了车辆乘坐的舒适性，故建议车辆尽量匀速通过桥梁，避免在桥上加速行驶。

5 结论

(1)根据车辆六轮间的相干函数关系和时间滞后关系建立的桥面非平稳随机激励模型，其功率谱密度与理论谱吻合得很好，前中后轮的时间滞后关系明确，且实际相干函数值与理论值也吻合的非常好，充分说明六轮相关桥面非平稳随机激励模型有效可靠。

(2)确定性桥面激励作用下，非平稳激励的桥梁和车辆振动响应大于平稳激励所产生的振动响应，且振动响应曲线波动大于平稳激励，桥梁响应曲线的峰值因车辆加速运动而相对滞后。

(3)采用蒙特卡罗法对多个桥面随机激励样本进行统计分析表明：平稳激励和非平稳激励对桥梁振动响应的均值影响很小，但车辆振动响应均值对桥面随机激励很敏感，非平稳激励增大了车辆振动响应。非平稳随机激励作用下的车桥振动响应标准差明显大于平稳激励作用，且车辆振动响应的标准差随着车辆的行进而增大，而平稳激励作用的振动响应标准差变化不大。

(4)随着车辆行驶速度的增加，因桥面不平顺引起的非平稳随机激励信号的幅值随时间 (速度)的增大而增大，且车桥系统的振动响应标准差随着车辆加速度的提高而增大。