例谈学生数学模型思想的培养
【摘要】本文论述培养学生数学模型思想的方法,提出巧用已有经验渗透模型思想,善借数形结合建立模型思想,引导灵活运用强化模型思想等教学策略,发展学生的建模能力,提升学生的数学核心素养。
【关键词】小学数学 《植树问题》 模型思想
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2020)06A-0094-02
新课标提出要注重培养小学生的数学核心素养,而模型思想是小学数学核心素养的重要组成部分。模型思想的建立是学生体会和理解数学与外部世界联系的基本途径,建立与求解模型的过程有助于提高学生学习数学的兴趣和应用意识。因此,在课堂教学中教师要重视培养学生的模型思想,不断发展学生的建模能力,提升学生的数学核心素养。
一、巧用已有经验,渗透模型思想
在对学生进行模型思想渗透时,教师要从现实生活出发、从实物出发,巧用学生已有的经验渗透模型思想,让学生更快地接受、更好地理解、更有兴趣地思考,那么渗透模型思想就不再是难题。
【教学片段1】《植树问题》导入环节
师:我们的教室里有许多数学奥秘,大家看看分组图,(图片中学生分成4组,最外边的两组都靠墙)你看到了数字几?
生(不约而同):4。
师:看到了数字4,那还能看到数字几?
生1:我看到了数字3、2、1。
师:哦?你说的数字3、2、1表示的是什么?
生1:小组的个数。
师:除了小组的个数还能看到什么?
生2:还能看到小组间的3条通道。
师:小组间的通道也就是小组的间隔。大家说4个小组之间有多少个间隔呢?
生(齐):3个。
师:那3个小组之间有几个间隔?2个小组之间呢?
(生依次回答2,1)
师:1个间隔。你们有谁发现了小组数和间隔数之间的关系吗?小组数比间隔数怎么样啊?
生3:小组数比间隔数多1。
师:想得真快,那间隔数比小组数呢?
生4:间隔数比小组数少1。
师:大家想想看,能不能用一个算式来表示小组数和间隔数之间的关系呢?例如小组数等于 ?
生5:小组数=间隔数+1。
师:间隔数等于 ?
生6:间隔数=小组数-1。
师:真聪明,把掌声送给自己。
渗透模型思想,教师要巧用学生已有的生活经验,借助他们熟悉的实物——分组和通道,通过“看教室内分组位置图——说一说看到的数字和含义——鼓励学生用自己的方式表达具体情境中小组数和间隔数的数量关系——建立模型”等教学活动,使学生在已有的生活经验中感受其中隐含的数学问题,从而帮助学生将生活问题抽象成数学问题,感知数学模型的存在。
二、善借数形结合,建立模型思想
培养学生的模型思想,不能是简单的模型建立、运用,还要从多方面帮助学生树立模型思想,让他们在不同的情境中学会建立模型、运用模型。因此,在日常教学中教师要定目标、找策略、分步骤创设建立模型、学习模型运用的教学环节。
【教学片段2】《植树问题》新知环节
师:一共要栽多少棵?同学们有不同的猜想,可以用什么办法验证呢?
生1:画图。
生2:我觉得不太好,在起点栽一棵隔5米,栽一棵又隔5米,栽一棵再隔5米,要画到什么时候呀?
师:太多了,画起来挺浪费时间的,还有什么好办法吗?
生3:我们把100米缩短成10米、20米来画可以吗?
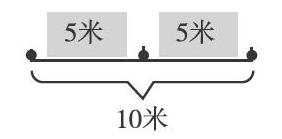
师:办法不错,在数学研究中遇到比较复杂的问题,可以先从简单一些的入手,也就是化繁为简。我们一起把100米缩短成10米,然后用线段图来画一画。
师:用点表示树,看明白了吗?谁能说说算式?
生4:10÷5=2(个),2+1=3(棵)。因为每隔5米栽一棵,用10÷5=2,线段图就分成了2段,所以间隔数就是2。
师:为什么加1?
生5:因为在这多了1棵,也就是栽了3棵。
师:这里1个间隔有几棵树?(2棵)两个间隔呢?(3棵)大家有什么发现?
生6:棵数比间隔数多1。
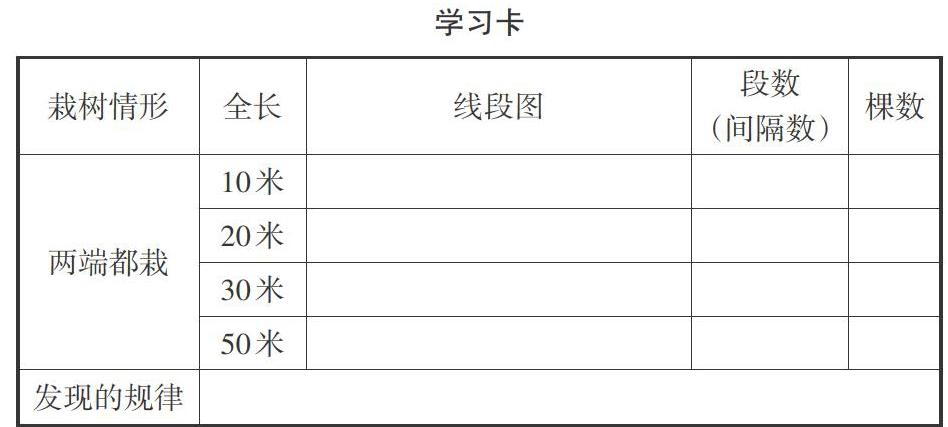
師:这个关系是否成立?大家继续画图验证一下,把画图的结果填到表格中。
学习卡
1.同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗?
(学生动手操作)
师:看着表格汇报一下20米可以栽几棵,有几个间隔?
生7:5棵,有4个间隔。
师:30米呢?
生8:7棵,有6个间隔。
师:现在谁能肯定地说一说棵数和间隔数的关系?
生9:棵数比间隔数多1,间隔数比棵数少1。
师:用数学语言来表达就是棵数=间隔数+1、间隔数=棵数-1,这是植树问题中两端都栽的情形。(板书)
师:同学们知道100米要栽几棵树了吗?
生10:100÷5=20(个),20+1=21(棵)。先算出有20个间隔,棵数等于间隔数加1,所以是21棵。
教师在帮助学生建立数学模型时,可以设置猜想一共能种多少棵、画线段图分析体会植树问题的规律、验证棵数和间隔数的关系并建构数学模型、运用数学模型列式解决100米种几棵树的问题等一系列数学探究活动,引导学生借助数形结合,在线段图上多次模仿植树并探索出两端都栽时“棵树=间隔数+1”的数量关系,让学生自主发现和建构模型,感受数学与现实生活的密切联系,体验成功的喜悦。
三、引导灵活运用,强化模型思想
灵活运用数学模型是强化学生建立模型意识、提升学生模型思想的基本途径。因此,用所建立的数学模型来解答生活中的实际问题,让学生能体会到数学模型的实际价值,体验到所学知识的用途和益处,从而进一步强化学生的模型思想。
【教学片段3】《植树问题》巩固环节
(一)基础练习
师:刚才我们发现了植树问题(两端都栽)棵数与间隔数的关系,现在要小试牛刀了,请快速抢答:(两端都栽)如果栽了10棵树,每两棵树之间挂一个灯笼,需要准备多少个灯笼?
生1:9个,因为间隔数=棵数-1,间隔数就是灯笼的个数。
师:(两端都栽)如果有15个间隔,应该栽多少棵树?
生2:16棵,棵数=间隔数+1。
师:反应都挺快,如果学校要在长150米的路两旁栽树,相邻两棵树之间的距离是6米,起点和终点都要栽,一共要栽多少棵树?
(学生列式计算)
生1:解答时我们一定要注意这是两端都栽的植树问题,并且是在路的两旁栽。算式是150÷6=25(个),25+1=26(棵),26×2=52(棵)。
师:审题非常仔细,这是常见的两端都栽情形的植树问题,刚学到的方法就能靈活运用,真不错!
(二)变式练习
师:教学楼每层楼梯有20级台阶,如果老师从1楼开始一共走了60级阶,现在老师在第几层呢?
生1:4楼。
生2:3楼。
师:哦,同学们有不同的意见,大家联系植树问题中两端都栽的情形,画一画图再列式解答。
(学生画图并列式解答)
生3:其实楼层变成点,每层楼的台阶变成一条线段,这个问题就是两端都栽的植树问题了,60÷20+1=4(层)。
师:真不错,不但学会了解决与植树问题相类似的问题,还懂得把楼层看成点、每层楼的台阶看成一条线段的解决问题策略。表扬你!
(三)开放练习
师:现在带领大家来到五彩田园看一看,你能提一些数学问题吗?课件出示:入园大道的一边每隔10米有一盏路灯(两端都有),一共有18盏路灯。
生1:入园大道有多长?
生2:从第一盏路灯走到最后一盏路灯,走了多少米?
生3:(18-1)×10=170(米)。
师:如果每两盏路灯的中间摆5盆花,一边要准备多少盆?
生4:(18-1)×5=85(盆)。
为了强化模型思想,这一教学环节安排了三个层次的练习,重在引导学生感悟很多实际问题都有类似的结论,只要借助模型并加以灵活运用就能解决问题,让学生进一步感受数学模型的魅力。
总之,渗透模型思想不是一朝一夕就能实现的,它需要一个长期的过程。因此,在教学中教师要善于挖掘数学知识中的模型因子,丰富建模内容和形式,启迪学生的建模方法,帮助学生理解模型的意义,真正提升数学学习能力,发展数学核心素养。
作者简介:杨莉玲(1980— ),女,广西玉林人,大学本科学历,一级教师,玉林名师培养对象,玉林市骨干教师,主要从事小学数学教育教学工作。
(责编 林 剑)

