初中数学探究性命题的类型与解题方法刍论

林艳玉

(福建省漳州市华安县第一中学 363800)

初中数学作为进一步提升学生数学基础、开启学生逻辑思维及发展性思维综合能力的阶段，对学生今后的学习有着更加重要的影响.因此，传统的教学模式已经不能够满足新时期初中生的发展需求.要想进一步夯实学生的初中基础知识，就要根据现阶段学生的实际情况出发，积极转变教学主体，以更加灵活的引导方式，来提升学生对基础知识灵活应用的能力，这对学生的长远发展会奠定更加有力的基础.

一、关于探究性命题类型的论述

关于探究性题目的具体概念，目前并无具体明确给定.但在一般情况下，探究性题目具有一定的开放性以及不固定性.因此，该类型题目可以为学生的独立思考与学习提供更加宽松的空间，同时对学生的各项思维能力也具有一定的培养作用，并通过不同方式的解题思路，能够让学生掌握更多的解题技巧.

1.从结论中给出条件

满足结论的条件并不是唯一的，是对学生探索、分析及反思能力的一种考验，具有一定的开放性特点.

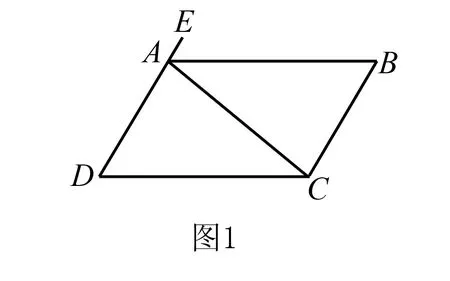
例1图1，如果想要得到AB∥DC，只需要满足何种条件.

该类型题目就是通过给出一定结果及条件，来分析相应的对象是否存在.该种答案有不存在和存在两种情况，因此主要的解题方法，就是通过演绎、推理、假设存在而得出结论，同时对题目做出准确有效的判断.比如要想证明AB∥DC，只需要找出内角角度以及其余两边是否平行，证明角与线之间的关系，即可做出准确解答.

2.结论开放型题目

3.简单开放型题目

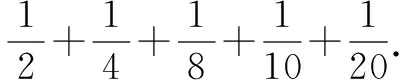
学生根据所学知识以及思维能力，可能会得出以下结论.

其一：直接通过通分方式进行相加减，然后再通过约分而得出正确结论：

其二：通过最小公倍数，来得出最后答案：

对于这两种解题思路来说，方法一主要是通过常规的计算方式，让分母统一，从而进行分子的相加减；而方法二更加体现了一种化归思想，虽然同样使用最小公倍数，但该种方法相对来说更为简便.

二、关于探究性命题方法的论述

1.灵活运用辅助线来提升论证能力

该类型题目是以几何图形作为题目背景的，通过设置相应的点与线，从而建立图形关系.

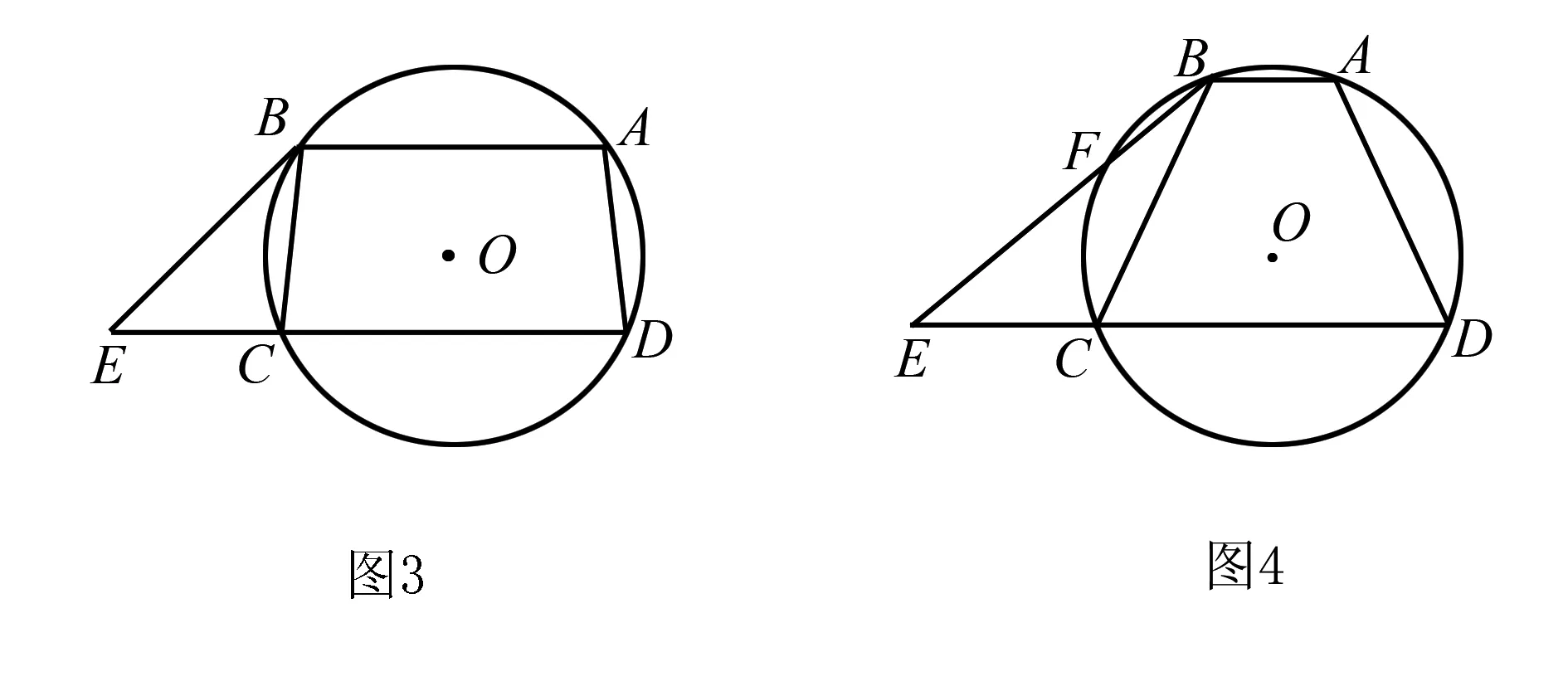
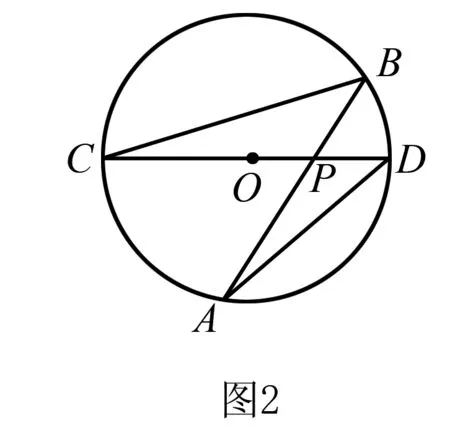
例4 如图3所示，四边形ABCD是⊙O的内接四边形，B是弧AC的中点，过B点的切线与DC的延长线交于点E.根据图形所示，(1)证明:BC·AB=AD·CE;(2)如图4，如果点E在CD的延长线上运动，点B在弧CD上运动，使切线EB变为割线EFB，其他任何条件依旧，那么需要具备什么样的条件，可以使原有结论成立.(注:只要求画出示意图注明条件，无需证明)

该类型题目是一道典型的条件探索问题，因此要以“执果索因”的方式进行解答论证.要想求证BC·AB=AD·CE，就要论证出△BCE∽△DAB，通过已给出的条件∠BCE=∠BAD外，还需要寻找更多条件，如∠CBE=∠BDA，来进行有效证明.

2.灵活运用基本知识寻求更多思路

学生思路的打开条件，是建立在对知识牢固掌握的基础上，这样可以使其发散思维及逻辑思维能力增强.因此，有效掌握基础知识，同时加强开放式习题的练习，可以不断突破学生的思维局限，有效提升学生灵活思考及分析能力.

例5 在一个多项式如16x2+1中，添加一个单项式，让其变为完全平方式，那么添加的单项式应该是什么？

分析如果要想使多项式16x2+1成为完全平方式，可以添加常数项，也可以添加二次项.

解答如添加8x，即可变成(4x+1)2；如添加-8x，即可变成(4x-1)2；如添加-1时，即可变成(4x)2；如添加-16x2，即可变成12.

例6 如图5所示，现已知△ABC内接于⊙O，CB为圆的直径，过点C作直线EF，要想使EF成为⊙O的切线，那么需要添加哪种条件？

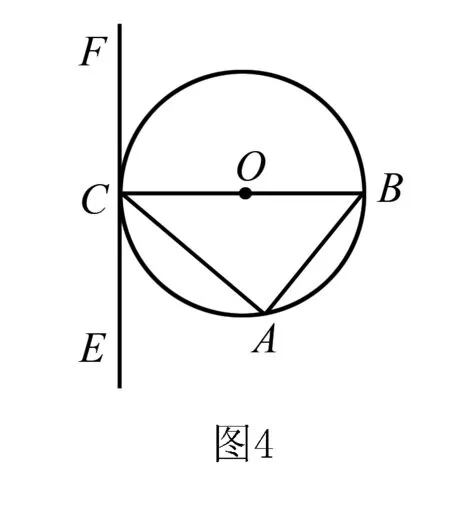
分析题目中已给出所需条件，因此又想EF成为⊙O的切线，分析出关键是CB⊥EF这个条件是否成立，如果成立即可证明.

解答条件为∠ACE=∠ABC、CB⊥EF、∠CAB=∠FCB、∠BCA+∠ACE=90°、∠ECB=∠BCF.

探究性题目具有更多的生动性、多样性及灵活性，以开放的形式及无固定模式的解题思路，来考验学生的思维能力、对基础知识的掌握能力及灵活应用能力，使学生通过该类型题目，能够提高其归纳、分析、想象、观察、类比、概括等综合思维方式，对提升学生整体的数学素养提供了更加有力的条件.