构造法在高中数学解题中的应用研究

张浩群

(广东省珠海市北京师范大学(珠海)附属高级中学 519000)

构造法就是根据题设条件或结论所具有的特征、性质，构造出满足条件或结论的数学模型，借助于该数学模型解决数学问题的方法.在高中数学解题指导中，构造法的应用能够激发学生主动调用函数、方程、几何图形、数列等知识，促使学生实现创新思考与逻辑探究，提升学生的解题能力.

一、构造法在高中数学解题中的应用类型

1.构造函数

在解题中，学生可以根据问题条件构造新的函数关系，将复杂的问题转化为熟悉的函数关系式，并利用函数性质进行解答.

例1 在实数范围内解方程：(x2-x+1)5-x5+4x2-8x+4=0.

分析该方程为高次的，直接展开超出所学范围，且过于复杂，因此并不可行，而利用函数，将高次方程转化为相应的函数，并结合函数的奇偶性进行分析则不失为一种简单易行的方法.

解析(x2-2x+1)5+4x2-8x+4=(x2-2x+1)5+4(x2-2x+1)=0，则令t=(x2-2x+1)，则将原方程构造函数f(t)=t5+4t，通过对f(t)的分析可知f(t)在区间实数范围与y轴仅有一个焦点，此时t=0,由此可推出x2-2x+1=0,x=1.

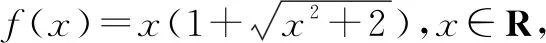
2.构造方程

方程与数量关系、函数等知识之间存在密切联系.在解题中根据条件构造出一个新的方程往往能够打开解题思路，获得更加便捷的解决方法.

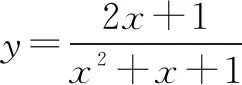
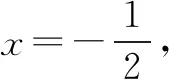
由上述题目可以看出方程在问题转化中有着更加灵活的应用，而教师应结合问题启发学生思考解题过程，即明确方程转化的条件，如何结合题目特点设计方程，讨论方程相关性质，即判别式与韦达定理，最后将方程结论转化为题目结论，完成对问题的有效解答.

3.构造几何图形

数形结合是数学学科的重要思想方法，在解题中，教师应指导学生将构造法与数形结合相融合，根据数量关系对图形进行与构造，利用直观图形实现对抽象问题的分析，以降低解题难度，提高阶梯效果.

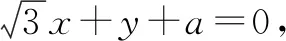
4.构造数列

数列模型具有一定的规律性，其在解题中能够更加清晰地呈现问题特点.在教学指导中，教师可以结合相应问题，指导学生构造等差数列或等比数列，利用数列性质进行解题.

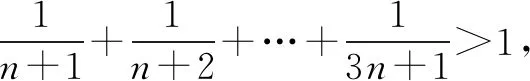
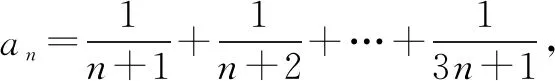
二、构造法在高中数学解题应用中需注意的问题

构造法在高中数学解题中的应用十分广泛，但是通过对学生解题过程与解题效果的观察，可以发现许多学生对于构造法的掌握存在问题，无法细致观察题目，在构造模型的过程中也常常一头雾水.针对此，教师在教学指导中，应注重方法，帮助学生掌握构造法的本质含义，并实现灵活自主运用.

在解题指导中，教师首先应注重对学生观察能力的培养.构造法属于创新思维方法，需要学生在细致观察中灵活调用所学知识.教师在教学指导中，应鼓励学生主动观察，为学生创设发现问题的情境，并结合问题渗透数学定理、解决数学难题的事例，融入一些富有趣味性的练习，让学生通过自己的观察、分析，发现题目之间的联系，并激发其主动构造的兴趣，提高观察能力.其次，教师应注重对学生思维发展过程的培养.构造法的运用是思维不断深化发展的过程，教师在教学设计中应精心编创问题，促使学生多角度地思考，经历假设分析、举例验证、反问推理等一些列抽象思考过程，让思路从思维定势的框架中跳出来，用一种全新的思维方式解答问题；此外，教师还应结合例题启发学生思考，鼓励学生表达，并在手脑口并用中加深印象，深化学生对数学知识的思考与应用，同时提升学生的思维品质.再次，教师应注重对学生举一反三能力的培养.举一反三是学生思维拓展的必要途径，在构造法的应用中教师可以对问题进行变式，利用相似的题目启发学生拓展思考，以提高知识灵活运用能力.例如在上述“构造函数”一节中，教师从方程拓展到不等式，不同的题目采取相同的思路，即构造函数，以启发学生对构造法应用的进一步思考，激发其结合其它问题尝试运用构造法的动力.最后，教师应注重对学生总结反思能力的培养.根据上述类型题举例可以看出构造法的应用范围之广，教师在教学指导中，应启发学生对多接触的典型习题进行总结，如构造函数、构造方程、构造几何图形、构造数列等，归纳解题步骤，探究构造法的应用思路，逐渐内化解题方法，将解题积累逐渐转化为数学思想方法，从而提升数学学习能力.

总之，在高中数学解题指导中，构造法是一种常见，且具有创新意义的解题思路.在教学指导中，教师应引导学生深入理解构造法的含义，理解构造的目的，并结合不同类题习题分析构造法的应用策略，促使学生在观察与思考中实现创新解答，提高解题能力.