卢比变换码在自由空间光通信中的应用
郝 源,吴 一,刘丽媛,刘宏展
(华南师范大学 信息光电子科技学院,广州 510006)
0 引 言
随着通信技术的高速发展,人们接触到的信息量与日俱增,这对信息传输过程中的有效性和可靠性都提出了更高要求。因此,作为现代通信系统中的重要组成部分,适当的信道编码方式对于数据包的有效且可靠传输起到了至关重要的作用。数字喷泉码是一种新的信道编码方式,它的编译码原理简单,易于实现,且对于不同的信道具有很强的适应性。
2002年,Michael Luby[1]提出了卢比变换(Luby Transform,LT)码,它是第1种真正具有实用意义的喷泉码(亦称无率码),其编译方法简单,编译码复杂度也相对较低。目前,LT码已被应用于自由空间光通信(Free Space Optical Communication,FSO)等领域[2]。本文将介绍LT码的基本原理,说明LT码在FSO中的研究进展,并对其未来研究方向进行展望。
1 LT码的基本原理
LT码性能的优劣主要由编码和译码方案决定。LT码编码过程的精髓是度分布函数,合适的度分布可以有效地降低编译码的复杂度。此外,优良的译码方案能降低译码开销并加快译码过程。
1.1 编码方案
LT码的编码方案如下:(1)从度分布Ω(d)中随机选择一个度值d;(2)从选定的k个源数据包中随机选择d个不同的数据包并对其进行异或运算;(3)重复步骤(1)和(2),即可获得任意长度的编码序列。
度分布是LT码理论的核心。Luby[1]提出了经典的鲁棒孤波分布(Robust Soliton Distribution,RSD),其数学表达式为

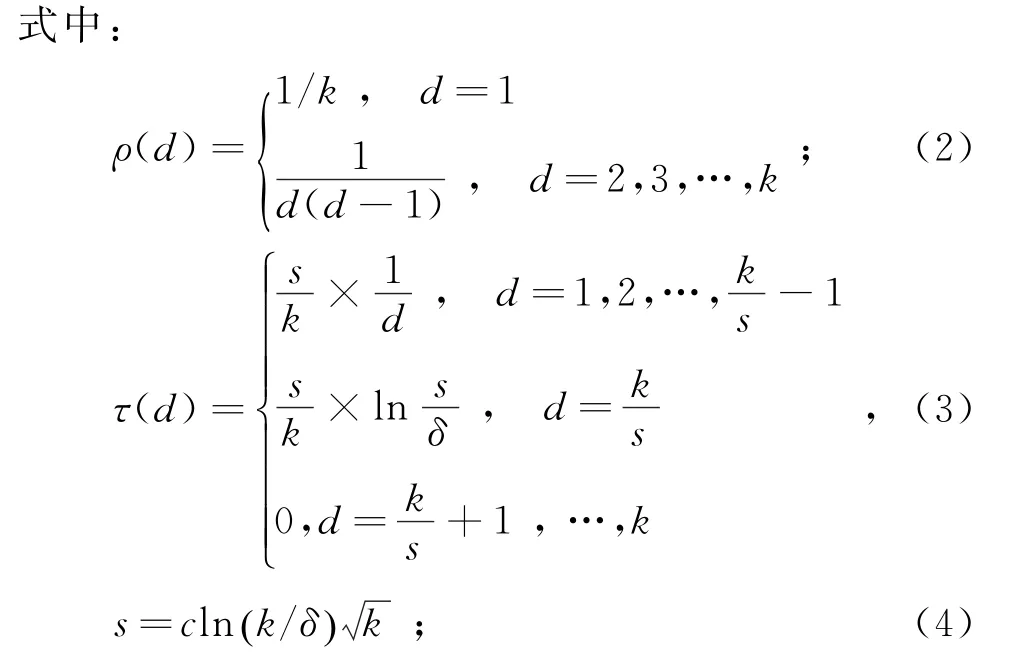
μ(d)为采用RSD进行编码时度值为d(d=1,2,…,k)的概率;k为源数据包的数量;c为0到1之间的常数;δ为未能完全恢复源数据包的概率。式(2)为理想孤波分布(Ideal Soliton Distribution,ISD)。
1.2 译码方案
经典的LT码译码方案如下:(1)找到度为1的输出符号oi,然后找到与之相邻的输入符号ik,便可直接译码得到ik=1,并在二分图上移除ik与oi相连的边;(2)找到与ik相连的所有编码符号oj,且令oj=oj⊕ik,同时在二分图上删除ik与oj相连的边;(3)重复步骤(1)和(2)直至无度值为1的编码符号。
2 LT码在FSO系统中的应用
2.1 研究现状
与传统无线通信相比,FSO具有更高的带宽、更好的保密性、更强的抗干扰能力和更高的传输速率,且无需向政府申请频率资源,因而已成为通信领域的研究热点,近年来引起了国内外学者的广泛关注。然而,由于大气湍流效应的存在,激光信号在大气信道中传输时会受其影响而产生较大的信号衰减甚至造成FSO链路的中断。为了克服大气湍流效应对FSO的不利影响,多种技术被提出,例如信道编码、分集和多跳中继等。在这些技术中,信道编码无需在现有FSO系统结构中进行改动,因而是最经济的解决方案,受到了学术界的广泛关注。相对于固定码率的传统信道编码,喷泉码的无码率特性使得针对FSO信道实现自适应传输成为可能[3]。此外,作为第1种具有实际应用意义的喷泉码,LT码的无码率性质也是其与FSO系统中常用编码方案——低密度奇偶校验(Low Density Parity Check,LDPC)码、Turbo码和Reed-Solomon(RS)码等相比的最显著优势,这4种编码方案的优缺点对比如表1所示[4-6]。

表1 LT码与FSO系统中常用编码方案的优缺点对比
虽然LT码最初是一种被应用于删除信道下的信道编码方案,但它也可被应用于噪声信道中。由于FSO信道以及深空通信信道(主要采用FSO这一通信方式)都是与加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道十分接近的理想信道[7-9],因此LT码在FSO系统和深空通信中也可取得较为优秀的性能。且研究LT码在AWGN信道中的编译码性能对于LT码在FSO系统与深空通信中的应用也具有较为重要的参考价值。
迄今为止,国内外研究者对LT码在FSO系统中的应用展开了较为广泛的研究。在国内,Yao等人[7]将LT码与LDPC码进行级联,并对这一级联码方案应用于深空通信中的性能进行了研究。重庆理工大学的曹阳课题组对LT码在FSO系统中的应用进行了一系列的研究,其中,文献[3]构造了一种将循环冗余校验(Cyclic Redundancy Check,CRC)码与LT码进行级联的编码方案(CRC-LT码),并对该方案在Gamma-Gamma信道下的编译码过程进行了仿真,仿真结果表明,在小幅提高译码开销的情况下,CRC-LT码的纠错性能与普通LT码相比有显著的提升(在信噪比(Signal-to-Noise Ratio,SNR)为20 d B的情况下约有2~3个数量级的差距);文献[10]分析了Gamma-Gamma信道下基于LT码的相干正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)FSO系统的性能,并通过仿真证明了在不同的湍流强度与传输距离下,与未编码相比,LT码均可小幅提高编码增益;文献[11]研究了LT码在多输入多输出(Multiple Input Multiple Output,MIMO)-FSO系统中的应用,且通过仿真得出在强、弱湍流环境下,与采用RS码相比,采用LT码能降低MIMO-FSO系统的误码率(Bit Error Rate,BER),数值仿真结果如图1所示[11]。由图可知,当BER约为10-6时,与RS码相比,LT码在弱与强湍流下分别有2.1和2.3 d B左右的编码增益。
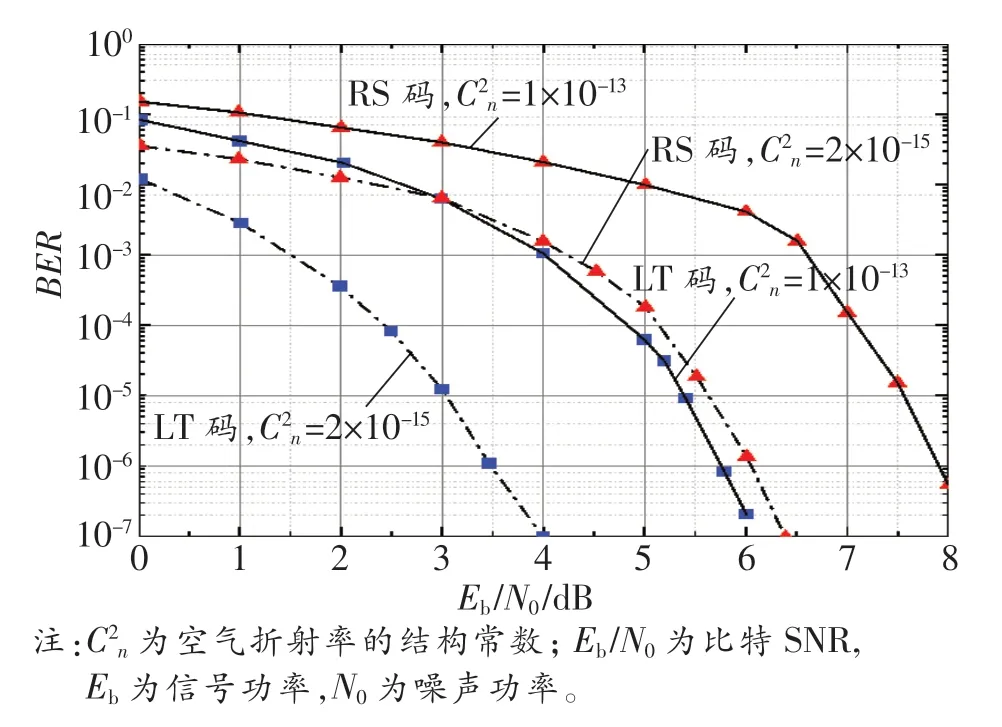
图1 LT与RS码在不同湍流强度下的BER性能对比

图2 LT码与LDPC码在AWGN信道下的BER性能对比
在国外,Prakash等人[12]将选择性地自动重传请求(Automatic Repeat reQuest,ARQ)与LT码相结合并应用于FSO系统中,实验结果表明,LT码能减少反馈重传的次数;Nayak[13]对LT码和博斯-查德胡里-霍昆格姆(Bose Chaudhuri Hocquenghem,BCH)码在射频(Radio Frequency,RF)-FSO混合系统下的性能进行了分析,分析结果表明,LT码能在中等和强湍流条件下以更小的能量消耗实现通信;Ando等人[14]提出并分析了一种精确的时间相关FSO信道模型,并通过仿真证明了码长足够长(至少为1 000)的LT码可以减少由光强闪烁引起的误码,从而有效地提高了FSO系统的性能;Mirrezaei等人[15]对LT码在AWGN信道下的BER和编码增益进行了研究与仿真,并将LT码与RS和Tornado码在译码开销和编译码复杂度等指标上进行了对比。基于文献[15]中的数值仿真结果,我们绘制了LT码与LDPC码在AWGN信道下的BER性能对比图如图2所示。由图可知,在SNR<3 d B时,LT码在BER这一指标上小幅优于LDPC(40,20)码。
作为整个LT码理论的核心和基础,LT码的度分布对其编译码复杂度和性能有着举足轻重的影响,从而也影响着FSO系统的通信性能,故设计得当的LT码度分布对于FSO系统至关重要。此外,LT码的译码算法也会直接决定其在FSO系统中的性能,故有必要选择合适的译码算法。近年来,国内外学者对LT码在FSO系统中的应用进行了更深入的研究,并从以上两个出发点对LT码在FSO系统中的性能进行优化。在这些研究之中,较为常见的思路有两种:(1)采用新型度分布函数;(2)对译码算法进行改进。
2.1.1 新型度分布函数
新型度分布函数包括开关度分布、泊松鲁棒孤波分布(Poisson RSD,PRSD)、固定度分布和修正转移鲁棒孤子分布(Improved Shift RSD,ISRSD)等。与传统的RSD相比,新型度分布函数在译码开销和编译码复杂度等指标上有着更为优越的性能。
荣子莉等人[16]采用了单开关度分布[17]与双开关度分布[18],并对弱和强湍流下FSO系统的性能进行了数值仿真,如图3所示[16]。由图可知,在强湍流条件下,当SNR为7 d B时,采用单和双开关度分布的LT码分别比采用RSD与二进制指数分布(Binary Exponential Distribution,BED)的LT码在BER这一指标上有着约1和4个数量级的提升;在弱湍流下,当BER约为10-5时,双开关度分布与单开关度分布相比拥有0.9 dB的编码增益,而后者与RSD或BED相比又分别具有约0.8和1.8 d B的编码增益。此外,与采用RSD和BED的LT码相比,采用单和双开关度分布的LT码在信道利用率上均有小幅提升。总体而言,与采用单开关度分布的LT码相比,采用双开关度分布的LT码在BER和信道利用率这两个指标上均有一定程度的提高。此外,在大多数情况下,采用双开关度分布的LT码的性能优于采用单开关度分布的LT码。
张勋等人[19]将文献[20]提出的新型度分布函数PRSD应用于MIMO-FSO系统,并通过仿真对比了采用PRSD的LT码和采用RSD的LT码在弱与强湍流信道下的BER。该文指出,在平均译码开销和平均度值这两个指标上,PRSD都显著优于RSD,具体数据如表2所示[19]。此外,如图4所示[19],BER为10-6时,在强和弱湍流条件下,采用PRSD和RSD的两种LT码相比分别具有约1.0和0.4 dB的编码增益,从而实现了MIMO-FSO系统通信性能的改善。
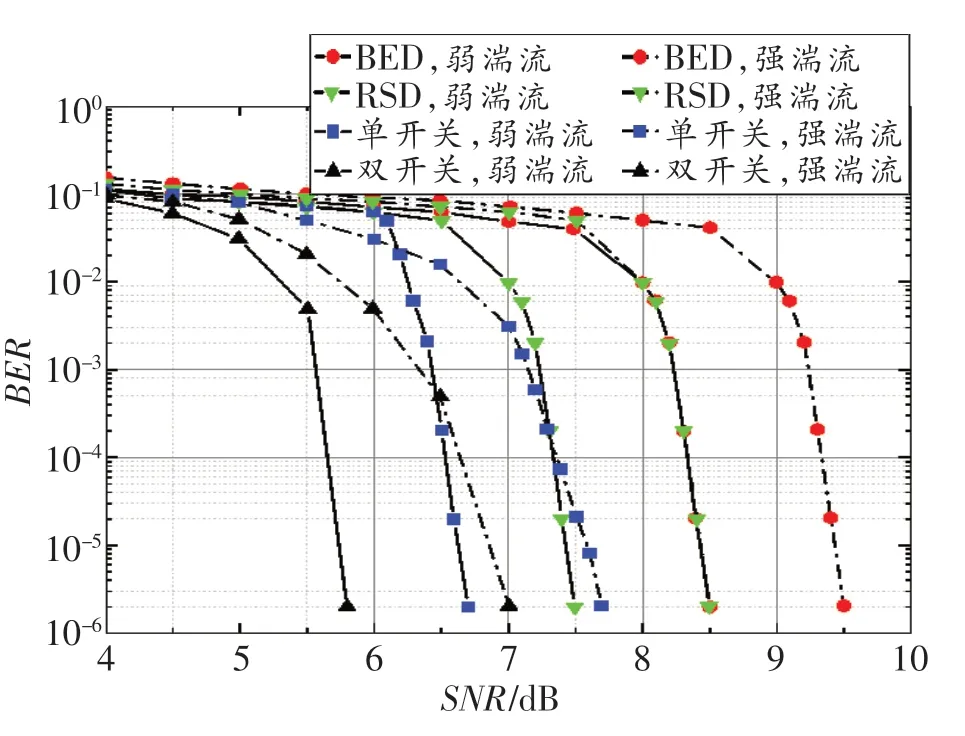
图3 几种度分布在不同湍流强度下的BER性能对比
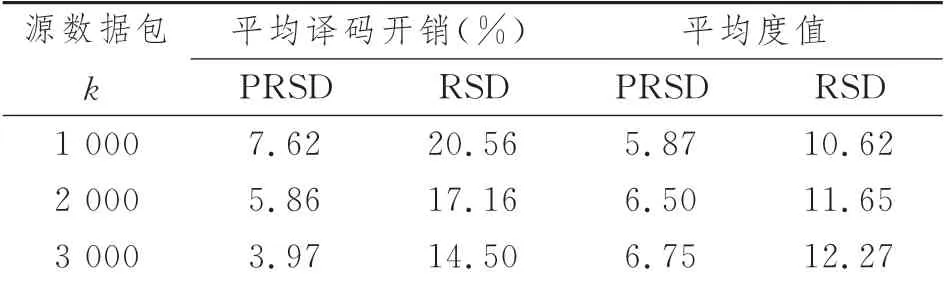
表2 PRSD与RSD的平均译码开销和平均度值
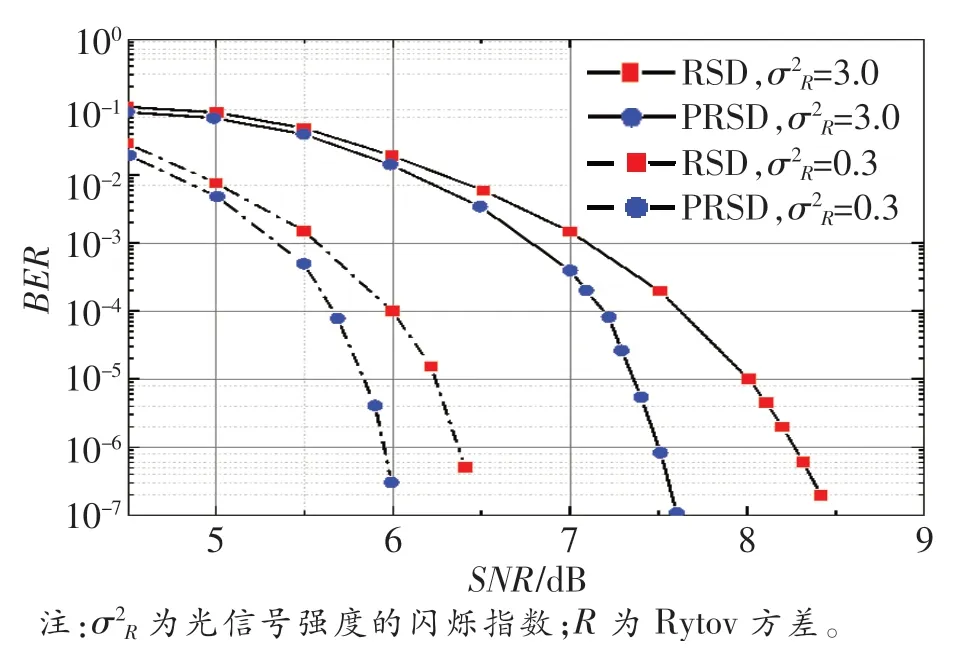
图4 采用PRSD与RSD的LT码在不同湍流强度下的BER性能对比
文献[21]引入了因子1/(K ln K)(K为码长),从而对泊松度分布[22]进行修改,构造了一种新型固定度分布函数,减小了小度值和大度值节点概率受码长增长的影响,从而在保证度分布概率值之和为1的前提下使得度值分布更加合理。仿真结果表明,当码长较小(K=500)时,该文提出的固定度分布有着优于RSD和泊松度分布的译码成功率,且在不同码长下(K∈(1 000,6 000))其译码成功率均高于泊松度分布。任发韬等人[23]在泊松度分布的基础上提出了一种新型的度分布ΩR,该度分布令度值为1与2的概率之和为50%,其他概率的值随机选取。仿真结果表明,当译码开销相同时,与采用传统度分布的多进制LT码相比,采用ΩR的LT码的译码失败概率明显较低,且码元进制的增大(8进制与4进制对比)会使得二者在译码失败概率上的差异更显著。
文献[24]将反馈思想与RSD结合,通过利用反馈信息对RSD进行修正得到了基于部分信息的转移RSD(Shifted RSD,SRSD)度分布函数。牛芳琳等人[25]提出最佳修正度分布函数并将其与SRSD结合进行参数调整后得到修正的SRSD(Improved SRSD,ISRSD),且仿真结果表明,ISRSD的反馈译码开销始终不大于SRSD,使得LT码的性能有所提升。文献[26]将采用ISRSD的LT码应用于MIMO-FSO系统中,在强湍流下且BER为10-6时相对于采用RSD的LT码得到了约0.8 d B的编码增益,提高了MIMO-FSO系统的稳定性。
在上述优化度分布中,通过联合几种不同的度分布而得到的开关度分布可以较为显著地提高LT码的性能,且通过选取不同的度分布(例如BED、ISD或RSD等)或设置不同的开关点,均有可能优化LT码的性能,这为LT码度分布的研究提供了一种新的解决思路。此外,与RSD相比,采取PRSD可以在显著降低LT码的平均译码开销与平均度值的情况下提高FSO系统的性能,故也是一种值得关注的优化度分布设计。
2.1.2 改进的译码算法
虽然LT码在删除信道下具有优秀的纠删性能,但FSO信道中存在的固有信道噪声会导致接收端必有误码产生,且SNR较低时会产生严重的干扰,故在采用为删除信道而设计的置信传播(Belief Propagation,BP)译码算法对LT码进行译码时,会导致接收端难以恢复准确的信息[27]。因此,LT码在被应用于FSO信道中时需要采取与删除信道中所采用方案不同的译码方案以降低BER。鉴于FSO与AWGN信道的高度相似性,AWGN信道中LT码译码算法的研究成果对于LT码在FSO系统中的应用具有较大的指导意义。
LT码运用于AWGN信道中时,较为经典的译码算法是基于对数似然比的置信传播算法(BP Algorithm based on Logarithm Likelihood Ratio,LLR-BP),该算法是一种软判决BP算法,在AWGN信道中可以取得比采用硬判决BP算法更快的迭代收敛速度和更低的BER。文献[28-30]均对采用LLR-BP算法对LT码在AWGN信道下进行译码做了研究。
此外,较为新颖的一种思路是将两种不同的译码算法结合起来,从而在不明显提高译码复杂度的情况下降低译码开销并提高译码速度。Kharel等人[31]将BP算法与高斯-若尔当消元法(Gaussian-Jordan Elimination,GJE)结合起来对码长较短(100或200)的LT码在AWGN信道下进行译码,并得到了优于BP算法的性能,数值仿真结果如图5所示[31]。由图可知,在SNR为8 dB且译码开销相同的情况下,采用BP-GJE联合译码算法与采用BP算法相比在BER这一指标上有约1.2个数量级的性能提升,且当SNR继续上升至10 dB时,该提升会更加显著,并且采用BP-GJE算法不会出现错误平层。

图5 BP-GJE与BP译码算法的BER性能对比
任发韬等人[4]将BP算法与部分最优算法(Optimal Partial Decoding,OPD)结合起来得到了一种优化的译码算法并运用于FSO系统之中,该优化算法先进行BP译码,在编码符号缺失度为1的情况下再采用OPD进行译码。该优化算法在译码复杂度略高于传统BP算法的情况下有效地减少了译码器的等待时间并显著地提高了译码速度,从而有效降低了湍流下FSO系统的通信时延。Bioglio[32]将文献[33]提出的即时高斯消元法(On the Fly Gaussian Elimination,OFG)进行改进提出了用于AWGN中软判决的OFG(soft OFG,sOFG)算法,该算法将块错误率较低的最可靠根据(Most Reliable Basis,MRB)算法与译码时延较低的高斯消元法(Gaussian Elimination,GE)联合起来,得到了显著低于传统BP算法的块错误率(Block Error Rate,BLER)。例如,当码长K=100、译码开销ε=1且SNR为5 dB时,采用sOFG算法译码的BLER为10-4,与采用BP算法的BLER(约10-1)相比有约3个数量级的提升。以上所提及的几种联合译码算法虽然会小幅增加译码复杂度,但是能换取BER或译码速度等指标的提升,进而提高FSO系统的性能。
2.2 未来研究方向展望
虽然LT码在FSO系统中的应用已经取得了一定的进展,但在一些方面仍有可以提高的空间。关于此方面的后续研究,在此提出一些展望:(1)目前为止,对于度分布的优化无法较好地适应LT码码长较短的情况,因此需要更深入地研究针对短码长LT码的度分布优化设计;(2)度分布的优化设计还主要受限于非系统形式的LT码,系统形式的LT码也是一个具有应用价值的研究方向;(3)对于较短码长的LT码而言,现有的译码算法在BER和译码开销等指标上仍有提升空间,因此可以对LT码的译码算法进行进一步的改善,亦或提出新型的译码算法;(4)LT码在复合FSO系统(例如MIMO-FSO、OFDM-FSO等)中的应用可被进一步地深入研究;(5)可以考虑将LT码与时下较为热门的深度学习相结合,例如利用深度强化学习来近似估计最优的度分布,从而获得LT码在FSO系统中的性能提高。
3 结束语
本文简单介绍了LT码的基本原理,叙述了LT码在FSO系统中的应用研究进展,从两种不同的思路重点介绍了LT码应用于FSO系统中的优化方案,并对LT码可以提高的方面进行了展望,以期能为LT码在FSO系统中的应用研究与发展提供一点帮助与启发。总而言之,随着对LT码研究的不断深入与相关理论体系的日益完善,LT码将会在FSO这一领域发挥更加重要的作用。

