基于FP腔的大量程超声解调系统研究

高在青,张示城,钮月萍,龚尚庆

(华东理工大学 理学院,上海 200237)

0 引 言

超声波传感器在非破坏结构健康检测、医学检测以及三维测量等方面具有重要应用意义[1]。近年来,基于光纤布拉格光栅(Fiber Bragg Grating,FBG)的超声波传感器因其具有体积小、灵敏度高、抗电磁干扰能力强和扩展性强等优势越来越受到广泛的关注[2-3]。

超声波检测的原理是测量超声波引起的FBG光谱移动,需要具有亚微应变的分辨率和高于千赫兹的带宽,其关键技术在于实现FBG光谱信号的高精度解调。文献[4-5]利用宽带光源和匹配FBG进行解调,但其系统噪声较大；文献[6-7]报道了可利用窄带光源减小系统噪声,但成本较高且无法多路复用,缺乏实用价值；光谱信号解调的灵敏度取决于光谱线宽,文献[8-9]利用π相移FBG(π-phase shifted-FBG,π-FBG)有效提高了探测灵敏度,然而π-FBG的窄线宽导致解调系统量程很小；为了提高量程,文献[10]提出了利用双法布里珀罗(Fabry Perot,FP)滤波器解调方案,但该方案中仅将量程提高了约两倍,且系统复杂、成本高,无法扩展。上述方案主要都是基于窄带边缘滤波法[1],普遍存在测量灵敏度和量程相互制约的问题。

为了解决上述问题,本文在文献[10]的基础上提出了一种基于FP腔和π-FBG的大量程解调方案。本文在理论上详细分析了利用FP腔的多个纵模和可调谐滤波器进行解调的原理,该方案具有高灵敏度,同时可以利用多个纵模构建解调器阵列有效地提高量程。本文还通过耦合模理论进行了数值仿真分析,仿真结果表明,本方案还具有很好的线性度且响应带宽可达到数百k Hz。

1 理论模型

图1所示为本文所提解调系统的原理图,宽带光源出射的光经循环器进入π-FBG被反射,反射光经循环器进入由FP腔、可调谐滤波器、光电探测器和控制器组成的解调部分。π-FBG的布拉格波长为

式中:neff为光纤纤芯的有效折射率；Λ为光栅周期。超声冲击会引起π-FBG的布拉格波长移动,且移动量与超声的声压ΔP(t)成正比[11],比例系数由光纤的材料决定。因此,通过检测π-FBG光谱的移动就可以测量超声信号。

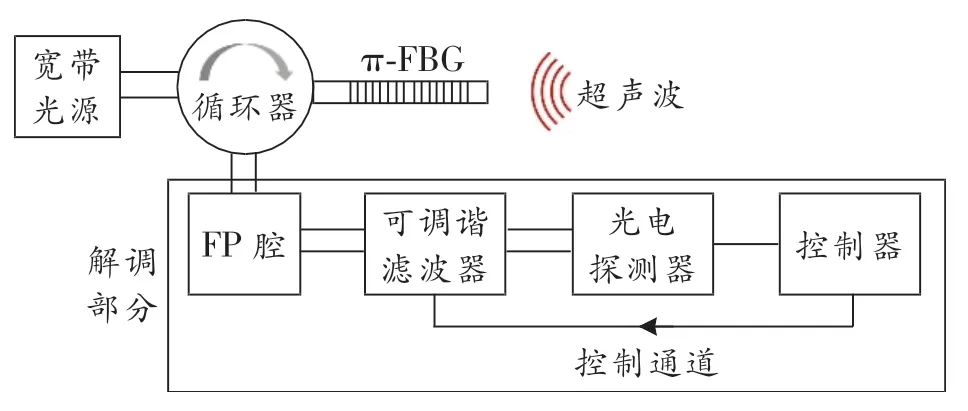
图1 解调系统原理图

图2所示为典型的π-FBG反射谱,图中b为窄峰带宽。通常可以利用窄带边缘滤波法进行解调,光谱的移动量为[1]

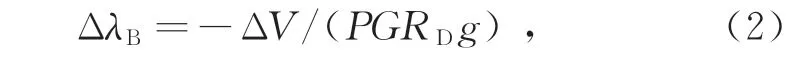
式中:ΔV为移动前后光电探测器输出电压的变化；P为输入光通过窄带滤波器后的功率；G为光栅的斜率(通常可近似为常数)；RD和g分别为光电探测器的响应因子和增益系数。边缘滤波法的解调灵敏度取决于G的大小,解调范围取决于b。对于窄带边缘滤波法,系统灵敏度越高就会导致量程越小,两者是相互制约的[8]。

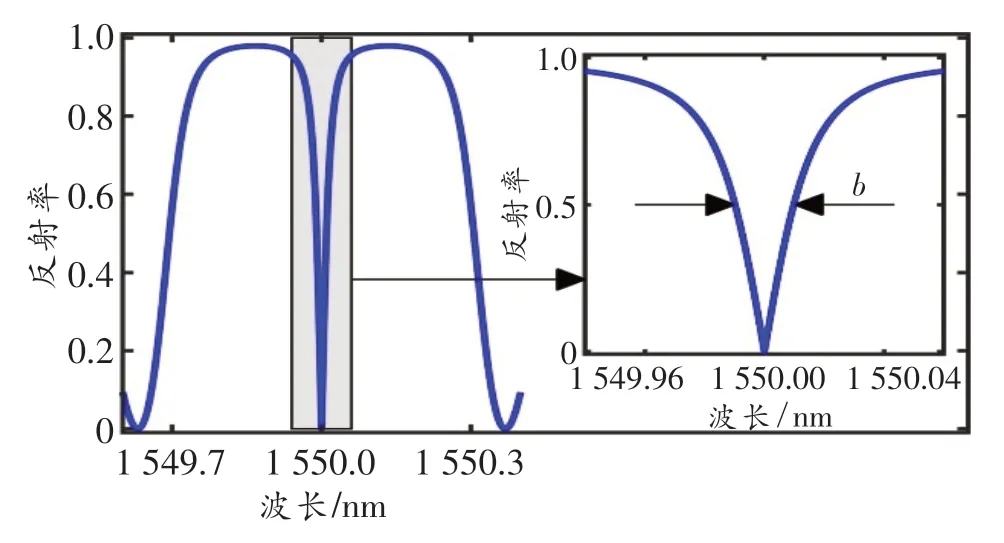
图2 π-FBG反射谱

本文提出了利用FP腔的多个纵模构建滤波解调器阵列扩大量程的方案。FP腔的纵模可看成是一个频率梳[λ1,λ2,…,λi,…,λN],其中λi为第i个纵模,N为用于解调的纵模数量。利用可调谐滤波器可使每一个纵模单独作为一个滤波解调器。可调谐滤波器由压电陶瓷(Piezoelectric Transducer,PZT)驱动,其带宽和FP腔的自由光谱区大小λFSR相当。通过调节PZT的电压,当可调谐滤波器中心波长与FP腔的某一个纵模波长相等时,就可测量出反射光通过该纵模后对应的光电探测器电压。在初始时刻 可 以 标 定 每 一 个 纵 模[λ1,λ2,…,λi,…,λN]对应的PZT驱动电压为[u1,u2,…,ui,…,uN],其中ui为第i个纵模对应的PZT驱动电压。测量时,通过快速扫描PZT的驱动电压就可得到每一个纵模对应的光电探测器输出电压[V1,V2,…,Vi,…,VN],其中Vi为第i个纵模对应的光电探测器输出电压。连续地周期性扫描就可以实时监测每一个纵模对应的光电探测器的输出电压变化。需要注意的是,这里每一个纵模对应一个可测量的波长区域。通过选择合适的FP腔参数,可使其λFSR与π-FBG反射谱带宽b相当。则不论π-FBG布拉格波长是多少,始终存在两个纵模分别位于窄峰的两侧可以同时用于解调,图3所示为π-FBG受超声波冲击移动前后的光谱图。因此,对于不同的布拉格波长,可以选择对应的两个纵模进行解调。本方案的量程主要受限于可调谐滤波器的波长调谐范围(通常可达数nm)。相比于文献[10]中的量程(约为0.2 nm),本方案中量程得到了极大地提高。

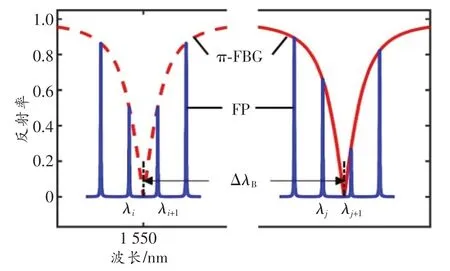
图3 π-FBG受超声冲击移动前后的光谱

下面我们详细分析如何根据光电探测器的输出电压来解调光谱移动量。假设初始时刻t0,模式λi和λi+1都处于π-FBG窄峰的半高峰位置,对应的光电探测器电压为=V0。在t0+Δt时刻,π-FBG反射谱移动了ΔλB,则此刻处于窄峰附近的纵模变为λj和λj+1,对应的光电探测器电压和表示为

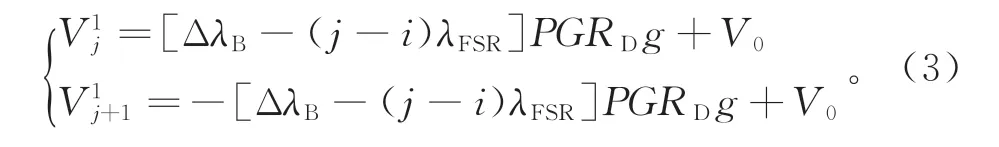
由上述分析可知,本方案可利用π-FBG窄峰附近的两个纵模作为一组解调器同时解调,这样不仅可以扩大量程,还可以将测量灵敏度提高两倍,并可以避免窄带边缘滤波法中存在的双值问题[2]。本方案的采样频率取决于PZT的响应频率fPZT和用于解调的纵模数量N,可表示为fPZT/N。通常fPZT可达M Hz量级,而N取决于待测信号的振幅。

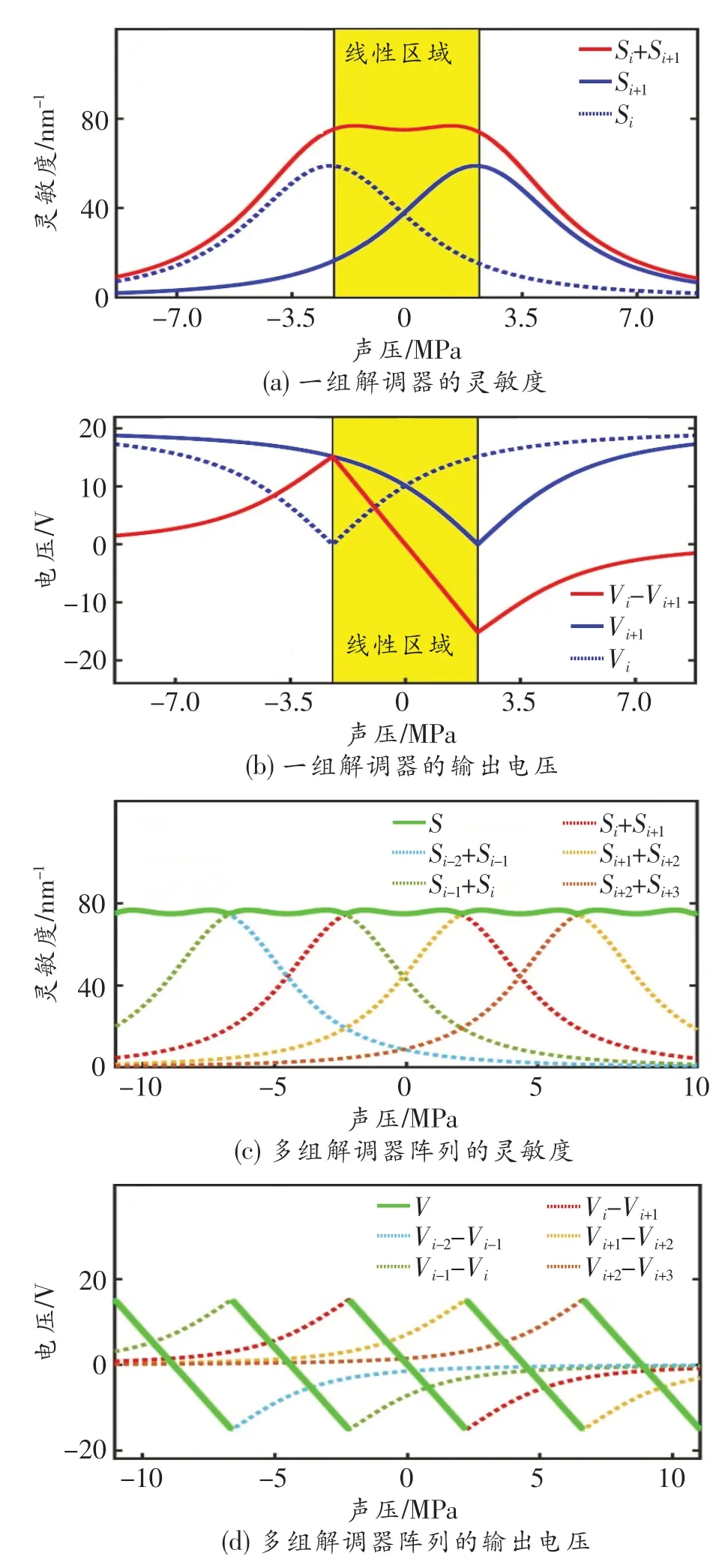
图4 系统灵敏度和输出电压随超声波声压的变化

2 数值仿真与分析

数值仿真中π-FBG的光谱变化可通过耦合模理论计算[12]。取π-FBG的光栅长度为5 mm,有效折射率为1.445 3,折射率调制深度为3×10-4,布拉格波长为1 550 nm,光纤材料的其他参数参照文献[11]。则根据所取参数可得π-FBG的带宽约为0.02 nm,半高峰位置的斜率约为39 nm-1。取FP腔长度约为6 cm,反射率为95%,则可得到纵模线宽约为0.32 pm,自由光谱区约为0.02 nm,因此对应的可调谐滤波器带宽可取为0.02 nm。对于光源和光电探测器,取光功率为3 d Bm,光电探测器响应因子为1 V/m W,增益系数为10,最小可分辨电压为0.03 V/Hz1/2。

我们首先对系统灵敏度和输出电压随超声波声压的变化进行了数值仿真,如图4所示。将纵模λi的灵敏度定义为(i=1,2,…,N),式中:r为反射率；λ为光波长。首先考虑一组解调器的情况,以λi和λi+1为例,如图4(a)所示。由图可知,单个纵模的灵敏度随声压的变化起伏较大,而两个纵模的总灵敏度Si+Si+1在较大区域内几乎保持不变,可以将该区域称为线性区域。因此对应的输出电压与声压呈现很好的线性关系,即系统具有很好的线性度,如图4(b)所示。然而一组解调器的线性区域仍然较小,当考虑多组解调器构成的阵列时,系统灵敏度S就可在整个量程范围内都几乎保持不变,如图4(c)所示。而由图4(d)可知,输出电压V则随着声压呈现周期性的线性变化。这是因为FP腔的纵模是等间距分布的,这也与式(3)和(4)相吻合。因此数值模拟结果进一步验证了理论模型的正确性,此外该方案还可以很好地解决窄带边缘滤波法测量线性度不好的问题。

下面讨论解调系统对于不同振幅和频率超声波信号的解调能力。假设PZT的响应频率为2 MHz,超声信号是一个包含10个周期的脉冲信号,如图5中红色实线所示,数值仿真采集的超声信号如图5中蓝色虚线所示。图5(a)从上到下分别对应声压为2、10和22 MPa的超声信号,其频率fs均为100 k Hz。由图可知,随着超声波声压振幅增大,每个周期内的采样点会减少,进而导致采样图形的失真。这是因为超声振幅的增大会导致用于解调的纵模数量增加,进而导致采样频率的减小。图5(b)所示为当fs分别为100、300和600 k Hz时声压为2 MPa的超声信号的采样结果。由图可知,对于振幅一定的超声信号,随着其频率的提高,同样的采样频率条件下,每个周期内的采样点也会减少,进而导致采样图形的失真。因此,最终采样图形的保真度取决于超声信号的频率和用于采样的纵模数量。根据数值仿真计算可知,当fsN≤fPZT/2时,采集的图形具有很好的保真度。此外,根据光电探测器的最小可分辨电压可以计算得到该方案的最小可分辨压强为4.4 kPa/Hz1/2,对应的最小可分辨应变为62 nε/Hz1/2,并且测量带宽可达百k Hz。文献[10]中使用的是切趾FBG,其灵敏度较低(με/Hz1/2量级),而本方案使用的π-FBG在灵敏度上也有一定提升。

图5 不同振幅和频率的超声信号采集

3 结束语

本文提出了一种基于FP腔和π-FBG的大量程解调方案。本方案利用FP腔的两个纵模作为一组解调器可以将探测灵敏度提高两倍,并且具有很好的线性度。扩展到多个纵模构建的解调器阵列,可以极大地提高量程,理论上量程可达数nm。数值仿真结果表明,该方案还具有较高的测量灵敏度,最小可分辨应变为62 nε/Hz1/2,并且具有数百k Hz的测量带宽。本方案可以有效地解决超声测量中测量灵敏度和量程相互制约的问题。