基于Agent的情感劝说交互的口碑更新模型

伍京华，郄晓彤，汪文生

(中国矿业大学(北京)管理学院，北京 100083)

0 引言

基于智能体(Agent)的劝说利用Agent的人工智能优势，能较好地模拟企业实际商务谈判、降低企业谈判成本，是商务智能中自动谈判发展到较为高级和智能化的阶段，正日益受到人们广泛关注[1-2]。情感影响着人们的认识、态度和决策等方面，对人类的劝说行为产生了重要影响。因此，将情感引入基于Agent的劝说，使Agent具备模拟人类情感的能力，可以使Agent的劝说行为模拟效果更佳，从而更智能化地模拟企业实际商务谈判[3]。

口碑是指人们在交互过程中逐渐形成的，对某个人物或事物的普遍观点和看法。反之，口碑的更新会对人们的实际交互产生重大影响[4-5]。基于Agent的情感劝说通过Agent之间的情感及劝说不断交互完成。因此，将口碑作为Agent模拟企业实际商务谈判的重点影响因素，并将其与基于Agent的情感劝说交互结合，研究基于Agent的情感劝说交互的口碑更新模型，能综合发挥Agent在人工智能方面的情感、劝说及口碑的优势，使基于Agent的情感劝说更加理性，谈判结果更接近各企业实际需求，具有重要的意义[6]。

在基于Agent的劝说研究领域，Rosenfeld等[7]结合理论论证建模、机器学习和马尔科夫优化技术，提出一种通过辩论对话说服Agent的新方法;Subagdja等[8]为了使劝说双方Agent的策略更具影响力，提出了具有说服力的Agent的协调框架;Kadowaki等[9]从平衡理论角度出发，研究了Agent之间的社会关系如何影响劝说的有效性，并开发了相应系统;WU等[10]提出了信任度的概念，阐述了基于Agent的劝说的信任模型，并建立了相应的评估机制;孙华梅等[11]将Agent的形式化表述模型和交互模型相结合，考虑让步幅度的影响，构建了相应的让步模型。以上文献结合不同理论和方法，对基于Agent的劝说进行了研究，提出了不同模型。虽然都在一定程度上提高了Agent的劝说效果和效率，但还没有考虑Agent的情感特性，更没有考虑基于Agent的劝说在口碑方面的人工智能优势。

在基于Agent的情感研究领域，Castellanos等[12]提出了基于Agent的情绪计算模型，通过Agent模拟人的认知和情感的相互作用，并设计了为Agent分配情感价值的机制;Wang等[13]分析比较了当前基于Agent的认知计算情绪模型，开发出了Agent模拟人的情感的系统;卢阿丽等[14]结合微表情识别技术等，提出了基于多Agent的情感识别的自适应性系统模型，并给出其框架图;伍京华等[15]结合心理学的情感强度定律，为基于Agent的情感劝说建立了情感的更新模型，并对情感强度量化计算，构建了相应的提议评价模型和信度评价模型;董学杰等[16]建立情感推理规则，提出了能够提高Agent的智能性和适应性的决策模型。以上文献虽然考虑了交互中的情感因素，但大多是对情感分类或建立相应规则，没有对交互中如何更新情感进行量化研究，因此不能真实模拟企业实际商务谈判。

在基于Agent的情感劝说交互研究领域，文献[17-18]采用隐马尔可夫模型识别真实人的情感状态，实现了基于Agent的人机交互系统，开发了具有模拟人的能力的基于Agent的情感虚拟人机交互模型;王玉洁[19]结合心理学相关模型，进行情感计算和建模，对人机交互进行了探索;宿翀等[20]在研究了Agent的情感计算的基础上，考虑了人机的情感交互，并提出了相应的学习算法，建立了情感交互学习的Agent模型;伍京华等[21-22]研究了基于Agent的情感劝说中的消极情感作用，并构建了相应模型。以上文献虽然从人的心理、情感计算和人机交互等角度出发，对Agent之间的交互进行了研究，但没有结合Agent的口碑很好展开。

在基于Agent的口碑更新研究领域，蒋帅[23]在复杂网络视角下，建立了在线口碑传播的Agent模型;Sweeney等[24]研究发现，口碑能否产生一定影响，取决于信息发送方和接收方之间的关系和所传递的信息量，以及各种情境因素;铁翠香[25]认为，接受方对网络口碑的信任评价是网络口碑能否影响其态度与决策的关键因素，而且Agent社会信任度的高低会对口碑信任度产生相应影响;陈蓓蕾[26]研究了互联网和电子商务背景下，受口碑影响的Agent的决策机制及模型;Barreda等[27]研究了OSN背景下Agent的信任、满意度、行为意图和口碑之间的关系，认为Agent之间的信任往往会对口碑更新有积极影响。以上文献虽然考虑了Agent的情感特性，但未提出口碑更新模型，也没有将基于Agent的情感劝说与口碑联系起来，因此更无法综合考虑口碑更新对基于Agent的情感劝说交互的影响。

针对上述问题，本文对模型作出假设，并对口碑更新机制进行分析，绘制了相应的机制图；采用直觉模糊数构建了交互评价向量，并结合前景理论，尤其是其中的价值函数，以及二分法，构建了相应算法，并以伪代码表示；基于标准评价向量，构建了口碑评价值算法，并考虑口碑随时间衰减的动态性，基于指数分布逆形式，对相应的口碑评价值权重进行了设定。综合以上研究，提出了基于Agent的情感劝说交互的口碑更新模型(Update Word of Mouth, UWOM)，并以伪代码表示，同时结合情感强度第一定律，设计了相应的情感劝说强度算法，进而给出了该模型下的提议更新算法。为验证该模型的合理性和有效性，设计了相应算例，并进行了分析，得出了相应结论和管理启示。

1 UWOM模型

为构建UWOM模型，首先需要进行相应假设，分析相应的口碑更新机制，其次要对机制中涉及的变量和算法等进行有效构建，并对相应权重进行设定，在此基础上得出该模型，进而根据该模型设计出相应的提议更新算法，从而更好地完成基于Agent的情感劝说交互，最终体现该模型的合理性和有效性。

1.1 假设

(1)买方Agent a与卖方Agent b采用情感劝说的方式，针对产品p进行交互。

(2)交互产品属性为价格、质量、付款期限和售后服务，其他属性也可根据该模型计算。

(3)买方Agent a和卖方Agent b同时给出产品p的各项属性提议值，且在首次交互中，参与情感劝说的Agent双方按照各自的期望值报价。

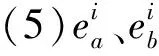
(7)如在第k轮次时，买方Agent a接受到针对价格和付款期限的提议小于或等于自身提议值，且针对质量和售后服务的提议大于或等于自身提议值，则达成一致，计算成交值，即最终买方和卖方提议值的中间值，结束情感劝说；否则继续，而卖方Agent b正好相反。

(8)T为最大轮次，如T轮劝说后，双方仍未达成一致，交互失败，结束情感劝说。

1.2 口碑更新机制

买方Agent a与卖方Agent b在每轮交互中，首先通过相应方法构建交互评价向量，并通过相应算法得到每个属性的交互评价向量值；其次将不同属性的交互评价向量值与其权重集成，得到每轮次的口碑评价值；最后通过相应方法对该口碑评价值进行权重分配，从而得到下一轮提议值，确定相应的口碑更新值，如图1所示。

1.3 基于直觉模糊数的交互评价向量构建

直觉模糊数在刻画不确定事件上具有一定优势[28]，自提出以来受到了众多学者关注，如文献[29]运用直觉模糊数来刻画突发事件的相关决策信息，研究了突发事件的应急决策方法。在基于Agent的情感劝说中，双方Agent的每次交互及其结果均具有不确定性，因此同样可以看成是突发事件。参照以上研究，本文运用直觉模糊数来构建相应的交互评价向量。

首先，构建交互评价向量直觉模糊集为F={〈y,μα(y),να(y),πα(y)〉|y∈Y}，表示双方Agent对产品属性的评价。其中：Y为非空集合；μα(y)为积极的交互评价值，表示对Y中元素y的满足程度；να(y)为消极的交互评价值，表示对Y中元素y的不满足程度；μα(y)∈[0,1]，να(y)∈[0,1]，0≤μα(y)+να(y)≤1,y∈Y[30]。

其次，将该交互评价向量通过直觉模糊数α=(μα,να)表示[30]，则在第k轮次Agent a和Agent b的交互中，Agent a对Agent b的产品属性i的交互评价向量为：

αki=〈μki,vki〉。

(1)

式中：μki为正面交互评价值;νki为负面交互评价值。

再次，根据文献[31]，可得相应的记分函数为S(α)=μα-να，精确函数为H(α)=μα+να。其中S(α)∈[-1,1]，并且如S(α1)α2；如S(α1)=S(α2)，则H(α1)>H(α2)时，有α1>α2，H(α1)=H(α2)时，有α1=α2。

最后，根据文献[32]，可得α1≥α2的可能度

(2)

若p(α1≥α2)≥0.5，则α1≥α2；若p(α1≥α2)<0.5，则α1<α2。

1.4 基于前景理论的交互评价向量算法

与效用理论不同，前景理论[33]中的决策者关注相对收益和相对损失，其核心为该理论中的价值函数，而这正是实际谈判参与方关注的焦点。因此，本文拟在该函数的基础上，结合基于Agent的情感劝说实际对其进行改进，进而构建相应的交互评价向量算法。

Agent在情感劝说中，对产品的每个属性都有期望值与保留值，若属性为成本型，则期望值为预期最小值，保留值为预期最大值；若属性为效益型，则期望值为预期最大值，保留值为预期最小值。采用二分法原理[34]，同时考虑Agent的期望值和保留值，并选取两者中间值表示Agent心理预期的中间值，以h表示，再以其为基值，可得交互第k次的Agent的相对理想收益SL(k)和相对理想损失SG(k)的计算公式如下：

(3)

(4)

另外，由式(3)和式(4)可得积极情感值μki和消极情感值νki的计算如下：

(5)

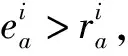
(6)

综上所述，可得Agent在第k轮的交互评价向量αk的算法如下：

αk=(ω1μk1+ω2μk2+ω3μk3+ω4μk4,ω1νk1+

ω2νk2+ω3νk3+ω4νk4)。

(7)

其中ω1,ω2,…,ωn为属性i的权重，采用较为普遍和有代表性的专家打分法确定[35]。

该算法可通过以下伪代码表示：

算法1交互评价向量算法。

IF期望值<保留值THEN

IF对方提议值<自身期望值THEN

相对理想收益=POW((属性i基值-期望值，γ))，相对理想损失=0;

IF自身期望值<=对方提议值<=属性i基值THEN

相对理想收益=POW((属性i基值-对方提议值，γ))，相对理想损失=0;

IF属性i基值<对方提议值<=自身保留值THEN

相对理想收益=0，相对理想损失=-λ*POW((对方提议值-属性i基值，β));

IF对方提议值>自身保留值THEN

相对理想收益=0，相对理想损失=-λ*POW((自身保留值-属性i基值，β));

ELSE

IF对方提议值>自身期望值THEN

相对理想收益=POW((期望值-属性i基值，γ))，相对理想损失=0;

IF自身期望值>=对方提议值>=属性i基值THEN

相对理想收益=POW((对方提议值-属性i基值，γ))，相对理想损失=0;

IF属性i基值>对方提议值>=自身保留值THEN

相对理想收益=0，相对理想损失=-λ*POW((属性i基值-对方提议值，β));

IF对方提议值<自身保留值THEN

相对理想收益=0，相对理想损失=-λ*POW((属性i基值-自身保留值，β));

IF期望值<保留值THEN

积极情感值=相对理想收益/(POW((属性i基值-期望值，γ))+ABS(-λ*POW((自身保留值-属性i基值，β))))；

消极情感值=-相对理想损失/(POW((属性i基值-期望值，γ))+ABS(-λ*POW((自身保留值-属性i基值，β))))；

ELSE

积极情感值=相对理想收益/(POW((期望值-属性i基值，γ))+ABS(-λ*POW((属性i基值-自身保留值，β))))；

消极情感值=-相对理想损失/(POW((期望值-属性i基值，γ))+ABS(-λ*POW((属性i基值-自身保留值，β))))；

交互评价向量=(SUM(属性i积极情感值*属性i权重)，SUM(属性i消极情感值*属性i权重))；

1.5 基于标准评价向量的口碑评价值算法

(8)

1.6 基于指数分布逆形式的口碑评价值权重设定

越久远的口碑，说服力越差，即口碑具有动态时间衰减性，因此本文借鉴文献[37]的指数分布的逆形式，对每次交互得到的口碑评价值分配权重，如式(9)所示：

(9)

式中t(k)为第k次交互占总交互次数T的权重，k越大，t(k)越大。

1.7 模型

综合以上研究，可得UWOM模型，即每轮交互后Agent的口碑更新值为

(10)

该模型可通过以下伪代码表示：

算法2口碑更新值算法。

口碑评价值=标准口碑评价值;

口碑评价值=标准口碑评价值-θ*ABS(记分函数(α));

口碑更新值=(口碑评价值-标准口碑评价值)*时间权重；

ELSE

口碑更新值=0;

1.8 基于UWOM模型的提议更新算法

首先，根据情感强度第一定律[38]，可得基于Agent的情感劝说交互的情感强度算法为：

q=kmlog(1+ΔV)。

(11)

式中：q为情感强度，其值用来衡量情感强度的大小；km为情感强度系数(一般取km=1)；ΔV为价值率的高差，

(12)

其次，将基于Agent的情感劝说交互的劝说强度用δ表示，为Agent在情感劝说过程中采取的交互策略对应的强度值。依据选择不同策略所进行的交互过程快慢，可将交互策略分为3类：0<δ<1为缓慢型交互策略；δ=1为均匀交互策略；δ>1为急迫型交互策略。

再次，将基于Agent的情感劝说交互的情感强度和劝说强度结合，可得基于Agent的情感劝说交互的情感劝说强度g的算法：

g=δ·q。

(13)

最后，在基于Agent的情感劝说交互中，由于第k次交互结果会对第k+1次交互产生影响，考虑以上情感劝说强度g，可得基于Agent的情感劝说交互的提议更新算法如下：

(14)

(15)

综合UWOM模型及该算法，可得相应的提议更新算法为：

(16)

2 算例和分析

为更好地阐述以上模型，以煤炭行业供应链管理中代表采购商的买方Agent a和代表供货商的卖方Agent b之间正在就某种煤炭交易进行情感劝说为例，假设如下：

(1)双方初始提议值如表1所示。

表1 买方Agent及卖方Agent初始提议值及对产品各属性的权重分配

(3)γ，β取值0.88，且λ=2.25[39]。

2.1 不考虑口碑更新的交互

为体现该模型的有效性，现将其与不考虑口碑更新的交互情况作对比分析。通过式(14)和(15)计算Agent a与Agent b第二轮后每轮提议值，如表2所示。

表2 不考虑口碑更新的交互

因此，最终在第八轮交互中，4个属性提议值均达成一致，情感劝说成功。

2.2 采用本文提出的模型的交互

表3 采用本文提出的模型的交互

因此，最终在第八轮交互中，4个属性提议值均达成一致，情感劝说成功。

2.3 结果分析

综上可得各项属性在不考虑口碑更新和本文提出的模型这两种情况下的最终交互值，如图2所示。

由此可见：

(1)两种情况下的情感劝说交互次数相等，均为八次。因此，采用本文提出的模型对交互轮次没有太大影响。

(2)两种情况下的最终成交价格值相等，且前者最终成交质量值及最终售后服务值均低于后者，而最终付款期限值则高于后者。因此，采用本文提出的模型能使最终结果对买方Agent更有利。

3 研究结论

本文将基于Agent的情感劝说与相应的口碑更新结合，展开了一定程度的研究。与已有研究相比，作出的改进及得出的结论如下：

(1)从交易中双方Agent关注的产品属性入手，着重考虑了实际交互过程中卖方Agent对买方Agent的影响，以及相应的口碑更新对基于Agent的情感劝说的影响，研究了交互过程中Agent的口碑如何更新及更新之后如何影响买方Agent的提议值。

(2)结合基于Agent的情感劝说实际，分析了模型的口碑更新机制，并指出了其中需要构建的变量和算法，以及需要设定的权重和模型对提议产生的影响，使该模型的构建思路清晰直观的呈现出来，从而为模型的构建打下坚实的基础。

(3)直觉模糊数在刻画不确定事件上具有一定优势，而基于Agent的情感劝说中，双方Agent的每次交互及其结果都具有不确定性，找到二者在这方面的契合点，采用直觉模糊数，对模型中口碑更新机制分析的交互评价向量进行构建，使该向量的表示更合理。

(4)结合前景理论中的价值函数，对交易双方Agent关注重点即收益和损失进行改进，同时结合二分法原理，计算了基于Agent的情感劝说的相对理想收益和损失，提出了相应的交互评价向量算法。与以往采用效用理论相比，更好地反映了现实交易中Agent的情感。

(5)基于标准口碑评价向量，同时考虑口碑的时间衰减性，运用指数函数的逆形式，对每次交互得到的口碑评价值进行计算，并分配相应权重，从而得出了UWOM模型。该模型体现了现实中口碑会随着时间推移而减弱的特点，因此更符合实际。

(6)结合情感强度第一定律，提出了情感劝说强度算法，并提出了没有考虑口碑更新的提议更新算法，最后综合该算法和所提UWOM模型，提出了相应的提议更新算法，从而从量化的角度，更全面和客观地综合反应了情感、劝说及口碑更新对提议更新的影响。

4 结束语

本文所提模型将情感、劝说和口碑更新融入了基于Agent的自动谈判中，使交互过程更加符合人的思维，更加智能化。通过本文的研究，可得出以下管理启示：

(1)交互过程中考虑口碑更新的影响，更能体现现实中历史行为对企业决策的影响，从而使企业管理者在考虑历史行为时所做出的决策对企业更有利。

(2)以前景理论为基础的价值函数考虑了企业管理者在实际交易中关注的重点即收益和损失，从而更好地反映了实际商务谈判中企业管理者对收益和损失的主观情感，进一步提高了基于Agent的自动谈判的自适应性，使该领域研究更具有实际价值。

(3)本文考虑的产品属性以价格、质量、付款期限、售后服务为例，而在实际商务谈判中，企业可以结合自身业务特点考虑更多属性，并为不同重要性的属性分配权重。因此，本文的研究具有较好的代表性和可扩展性。

(4)本文算例虽然以煤炭企业为例进行研究，但该模型同样适用于煤炭供应链上的其他环节，也适用于其他领域的商务谈判，因此具有较好的通用性。企业管理者可以在本文模型的基础上，结合自身业务特点，开发出适合自己企业的系统，提高企业管理效率。

本文初步将情感、劝说和口碑更新与基于Agent的自动谈判结合，研究了相应的口碑更新模型，由于是对该领域的初步探索，因此还存在以下不足和值得进一步研究的方向：

(1)模型着重探讨买方Agent在情感劝说中考虑口碑的情况，而卖方Agent也同样可以考虑口碑。下一步将在此基础上研究双方Agent都考虑口碑的相对复杂的情况。

(2)模型采用算法的可靠性还有待改进，如直觉模糊数。因此下一步将考虑引入更为复杂的理论或方法，改进其中的算法，以提高模型的合理性和有效性。

(3)口碑在更新之后，还会在Agent体系中进行传播，传播给其他接受口碑的Agent，而口碑如何进行传播以及怎样影响口碑接受Agent的决策是企业管理者更为关注的问题。未来，将进一步对基于Agent的情感劝说的口碑传播模型等展开研究。