时间依赖型同时取送货VRP及超启发式算法
张景玲,刘金龙,赵燕伟,王宏伟,冷龙龙, 冯勤炳
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
0 引言
在当今激烈的市场竞争中,越来越多的企业趋向为客户提供全生命周期的产品及服务,如家电、食品、汽车行业,这就要求企业在保证配送时效的同时,对客户点进行配送与回收服务。传统车辆路径问题(Vehicle Routing Problem, VRP)的研究不能描述城市物流配送过程中同时取送货的特点,越来越多的学者转向对其分支问题——同时取送货的车辆路径问题(Vehicle Routing Problem with Simultaneous Delivery and Pickup, VRPSDP)进行研究。
Min[1]于1989年首次提出VRPSDP用于解决公共图书馆问题;Poonthalir等[2]从路径最短的角度对混合回程的车辆路径问题进行建模,并考虑车辆巡航以及空载时燃油消耗及碳排放;Ninikas等[3]研究了一种动态VRPSDP,在执行预制定的配送方案过程中实时接收动态的取货请求;Lin等[4]提出一个集成了混合邻域搜索算法的决策支持系统(Decision Support System, DSS)原型来解决离线和在线需求的动态车辆路径问题;Hu等[5]研究了货物不兼容情况下,具有不确定性送货和确定性取货的动态闭环VRP;Wang等[6]等以降低人力成本、运输成本以及提高客户满意度为目标,采用邻域搜索算法对带软时间窗的VRPSDP进行多目标优化;王超等[7]提出一种离散布谷鸟算法(Discrete Cuckoo Search, DCS)算法,以最小化分配成本与行驶成本之和为目标对硬时间窗的VRPSDP进行建模并求解。上述研究很少涉及时间依赖型的VRPSDP,现有时间依赖型车辆路径问题的研究多集中在无取货的VRP。Malandraki等[8]对时间依赖型车辆路径问题(Time Dependent Vehicle Routing Problem, TDVRP)做出了具体描述,首次提出了三段的行程速度分段函数,将VRP扩展为TDVRP,揭开了对时间依赖型问题的研究的序幕;Figliozzi[9]分析了市区的早晚交通高峰,引入了1~2.5的旅行速度,使得TDVRP更具有实际的应用价值;穆东等[10]在主从式并行模拟退火算法框架下,使用4种邻域搜索法求解TDVRP,优化目标为最小化配送车辆数量与总行驶距离;Zhang等[11]将行程速度分段函数引入VRPSDP,并设计了集成蚁群与禁忌搜索的新型算法(Ant Colony System and Tabu Search algorithms, ACS-TS)求解该问题。现有VRPSDP研究假设车辆匀速行驶,忽略了车速对配送活动的影响,导致VRPSDP模型不能很好地描述城市物流配送速度时变的特点,因此本文研究时变车速对配送成本的影响,建立了时间依赖型同时取送货车辆路径问题(Time Dependent Vehicle Routing Problem with Simultaneous Delivery and Pickup, TDVRPSDP)模型。
超启发式(Hyper-Heuristics, HH)算法因其具有一定的通用性可用来求解不同领域的组合优化问题[12],获得了越来越多研究者的关注。HH算法框架包含高层启发式策略(High-Level Heuristic, HLH)和底层启发式算子(Low-Level Heuristics, LLH)两个层次。HLH包含LLH的选择策略(Selection)以及解的接受准则(acceptance criterion)。通过HLH管理或操纵一系列LLH以选择和产生新的启发式算法对解空间进行搜索。Chen等[13]提出了基于蚁群的HH算法用于解决锦标赛问题,采用蚁群算法来管理和操纵LLH以获得新的启发式算法;Burke等[14]针对教育时间表问题提出了基于禁忌搜索的HH算法,采用禁忌搜索(Tabu Search, TS)方法来获得新的LLH的组合而成的新的启发式算法;Dokeroglu等[15]提出了一种集成模拟退火、禁忌搜索和蚁群优化算法寻找最优解的HH算法去解决二次分配的问题(Quadratic Assignment Problem, QAP);Sabar等[16]使用一种基因表达编程算法,根据解的评价自动选择高层启发算法控制LLH搜索最优解;Zamli等[17]提出一种集成的HH算法,采用禁忌搜索作为高级元启发式和4种低级元启发式的强度,包括基于教学优化、全局邻域算法、粒子群算法和布谷鸟搜索算法选择最适合LLH;Asta等[18]提出多级选择的超启发算法,且引入了学习机制;Özcan等[19]使用群体决策策略作为超启发算法的移动接受准则,且每次迭代的接受准则不限于一种。HH算法不但可求解问题种类广泛,框架设计灵活多样,而且求解组合优化问题时,可以在较短的时间获得可接受解。冷龙龙等[20]以量子进化策略作为超启发式算法的高层学习策略,并结合滑动窗口机制实现底层算子的准确搜索,提高算法性能。
鉴于超启发式算法在求解组合优化问题上的优良性能,本文提出了基于禁忌搜索的超启发式算法,将禁忌搜索机制作为高层选择策略用于搜索LLH空间,根据LLH历史表现进行评分并逐代更新禁忌表,每次迭代选取最佳算子对解空间进行搜索,从而实现高层策略对底层算子的有效控制。
1 时间依赖型同时取送货的车辆路径问题
1.1 问题描述
TDVRPSDP描述如下:给定一个配送中心,一个车辆集合,一个客户点集合。车辆从配送中心出发为同一城市不同位置的客户点进行配送与回收服务。配送过程中,车辆按顺序依次访问各客户点,车辆到达客户点进行配送的同时完成客户点的回收取货需求。车辆应在客户允许的时间范围内提供服务,完成客户点的访问任务后最终返回配送中心。所有车辆具有相同的容量,且配送车辆在不同的配送时间段有不同的旅行速度。当车辆早于客户点的时间窗要求到达该客户点时,配送车辆进行等待,产生惩罚成本计入总成本。
构建模型要求满足以下条件,模型参数如表1所示。

表1 参数符号定义
(1)装载量限制。在任何时刻,车辆的载重量不得超过车辆的最大载重。
(2)车辆路线约束。车辆从配送中心出发,完成配送后回到配送中心。
(3)节点约束。车辆进入某个客户节点,也必须从该节点离开。
(4)配送车辆服务约束。一辆车可以为多个客户服务,但一个客户点只能被一辆车服务。
(5)客户点时间窗约束。配送车辆必须在客户点的时间窗要求内访问该客户点,提前到达客户点进行等待产生惩罚成本。
1.2 时间依赖型路网
TDVRPSDP是研究车辆旅行速度随时间变化的一类车辆路径问题,同样属于NP-Hard问题,其求解更为复杂。本文采用了Zhang等[11]的行程速度分段函数,将总配送时段分为早高峰(morning Rush hour)、中午平峰(non-rush hour)、晚高峰(evening rush hour)三段,且三时段时长相同,每个时段车速不变,行程距离随不同的旅行速度线性变化,如图1所示。
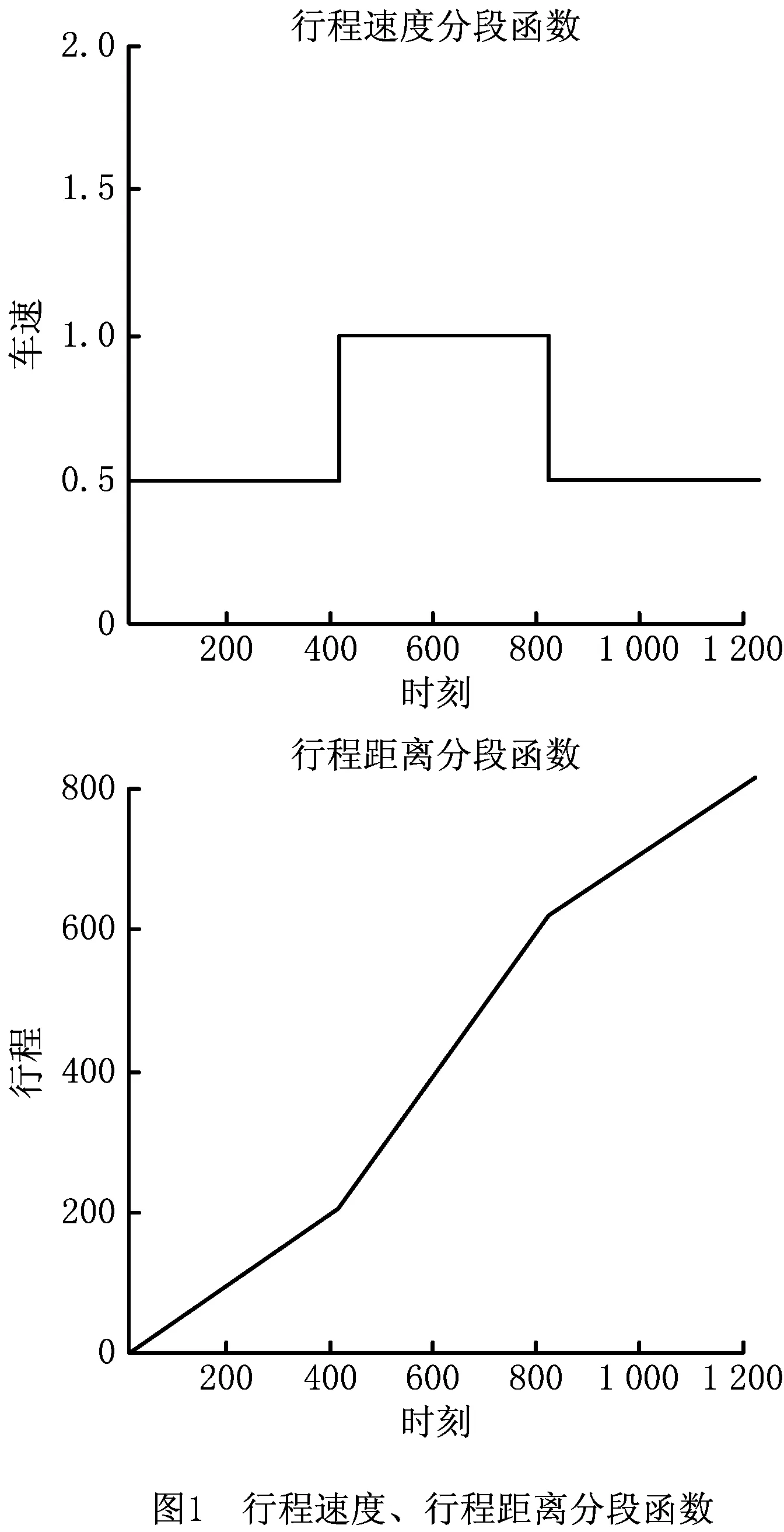
本文对TDVRPSDP的目标函数值提出如下计算方法,具体步骤为:
步骤1将配送时间段[e0,l0]以时间一定的间隔等分为R个时段,每个时段上对应于车辆的行驶速度,即分段函数形式的速度时间函数。
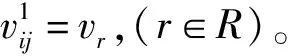
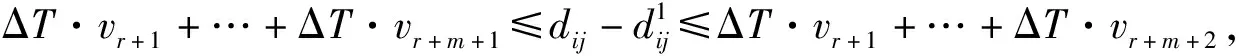
因此,得到车辆从客户点i离开到达客户j时跨越的w个时间段的速度、行驶距离以及配送时间为:
(1)
(2)
(3)
(4)
步骤4分段带入计算车辆旅行成本以及车辆等待的惩罚成本。车辆离开客户点i到达客户点j的旅行成本以及等待时间惩罚成本为
(5)
1.3 数学模型
本文采用文献[11]所建立的TDVRPSDP模型,其目标函数是总成本最小,包括车辆租赁成本、旅行成本以及惩罚成本。数学模型如下:
(6)
s.t.
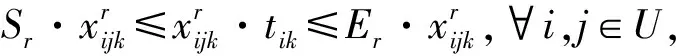
∀k∈V,∀r∈W;
(7)
0≤Lijk≤Q,∀i,j∈U,∀k∈V;
(8)
(9)
(10)
ei≤tik≤li,∀i∈U,∀k∈V;
(11)
(12)
(13)
(14)
∀i,j∈U,∀k∈V;
(15)
∀j∈U,∀k∈V。
(16)
其中:式(6)为TDVRPSDP的目标函数,表示总成本最小化,包括车辆租赁成本、车辆旅行成本以及车辆等待的惩罚成本;约束(7)保证了客户在特定的时间间隔内被访问;约束(8)配送车辆在任意的时刻都满足容量约束;约束(9)车辆出发时的载重等于所有要访问的客户点的需求量总和;约束(10)车辆回到配送中心的时的载重量等于所有已访问的客户点的回收量的总和;约束(11)车辆访问客户点的时间窗约束;约束(12)保证每个客户点必须且仅仅被访问一次;约束(13)保证每条路径,从配送中心出发回到配送中心的是同一辆车;约束(14)保证每辆车仅被使用一次;约束(15)保证了车辆从客户点i出发到到达客户点j的时间等于车辆旅行时间加上等待时间;约束(16)保证配送车辆访问客户点i前后载重的变化等于需求量减去回收量。
2 基于禁忌搜索的超启发式算法设计
超启发式算法通过管理或操纵一系列LLH,以选择和产生新的启发式算法对解空间进行搜索。因此,算法的关键是如何设计高层策略和底层算子。本文提出的基于禁忌搜索的超启发式算法将从以下5个方面开展研究:①初始解的构成;②底层启发式算子设计;③算法高层接收准则及选择策略设计;④超启发式算法框架设计;⑤算法复杂性的计算。
2.1 初始解的构成
一个完整的解表示全部路径的集合,它包含所有客户点,每个客户点只出现一次,并划分为k条路径,由k辆车同时配送,每条路径包含一定数量的客户点,路径的起始点都是配送中心。可行解要求在每条路径的任一时刻,配送车辆都要满足容量约束以及客户时间窗约束。
以配送中心为起点构造初始路径。判断最近的客户点是否符合时间窗以及车辆容量约束,若不满足则隔离该客户点并选择下一个最近的客户点,否则将其纳入当前路径,并将所有隔离客户点解除隔离,重复此步骤直至所有客户点都不满足约束,关闭该路径并开启新的路径。当所有客户点都被安排到路径内时,关闭最后一条路径。最后对产生的可行解执行若干次变异,得到丰富多样的种群,再选择较优的解作为初始解组。
2.2 底层启发式算子设计
LLH要根据具体的问题进行设计,一般分为3类:局部优化算子(Local Research, LLH-L)、变异算子(Mutation, LLH-M)和破坏与重构算子(Location-based Radial Ruin, LLH-LR)。VRP问题中底层启发式算子设计如表2所示。

表2 底层启发式算子设计
表2中:Adjacent(General)Swap表示相邻(不相邻)节点交换位置;Single(Block)Insertion表示一个(两个相邻)节点移动到两相邻节点之间;Shift(m,0)表示当前路径中m个相邻节点插入另一条路径中;Swap(m,n)表示当前路径中的m个相邻节点和另一条路径中的n个相邻节点互换位置;Inside-2opt表示连接两客户节点的路线反向后替换原来的路线。
2.3 解的接受准则及选择策略设计
2.3.1 接受准则
接受准则(acceptance criterion)用于判断是否接收子代解取代种群中的个体。接收准则设计的合理与否直接影响超启发算法收敛速度与优化精度,若执行算子后得到改进解,则总是接收;若得到非改进解,则以一定的概率接收。本文高层策略选择模拟退火(Simulated Annealing, SA)作为接收准则,非改进解以概率P接收,
P=exp(ΔE/Tk),
(17)
Tk+1=Tk·β。
(18)
2.3.2 选择策略(Selection)
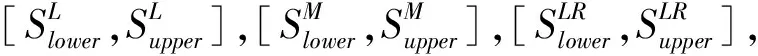
同时,本文使用以下两种选择策略作为对比:①简单随机(Simple Random, SR),每次迭代随机选取算子;②随机下降(Random Descent, RD),随机选择一个算子,一直重复使用该算子直到解没有改进,然后再选择其他算子进行搜索直到满足停止条件。
2.4 算法框架设计
算法采用种群机制,种群规模NI,为保证每次迭代以合理的概率选择LLH、接受非改进解,设计出如图2所示算法流程,具体步骤如下:

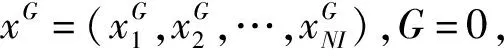
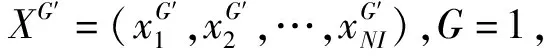
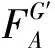

步骤6更新禁忌表。根据算子得分SG=[S1,S2,…,S20],计算评价分数SL、α·SM、α·SLR,更新算子禁忌表,并根据不在禁忌表内的算子的得分,使用轮盘赌策略选择算子hG。
步骤7退出迭代。若G>Gmax,算法结束,输出最优解,否则转步骤2。
2.4 基于禁忌搜索的超启发式算法复杂度分析
根据上述流程,算法的复杂度包括:底层算子执行复杂度、解的接收执行复杂度、算子评分与禁忌表更新执行复杂度、选择策略执行复杂度、适应度值计算执行复杂度、最优解更新执行复杂度和初始化操作执行复杂度。本文基于禁忌搜索的超启发式算法参数如下:种群规模为NI、迭代次数Gmax、客户数量为N、车辆数量为K、底层算子个数为NL以及配送时间分段数量R。
(1)底层算子执行复杂度 LLH-L和LLH-M算子完成客户点的插入操作,并计算适应度值,因此复杂度为O(O(1)+O(R·N2));LLH-LR算子重构一个可行解,则复杂度为O(O(N2)+O(R·N2))。算法采用种群机制,因此对于LLH-L和LLH-M的执行复杂度为O(NI·(O(1)+O(R·N2))),对于LLH-LR执行复杂度为O(NI·(O(N2)+O(R·N2)))。
(2)解的接收执行复杂度 与最优解进行比较,判断是否接收,复杂度为O(NI·O(1))。
(3)算子评分 对每个算子进行加分或扣分,复杂度为O(NI)。
(4)禁忌表更新执行复杂度 按评价分数将算子排序,直接插入排序的复杂度为O(NL)。
(5)选择策略执行复杂度 轮盘赌选择算子,复杂度为O(NL)。
(6)适应度计算复杂度 对于时间依赖型车辆路径问题,需要计算车辆由客户点i出发到达下一个客户点j所跨越的时间段R,分时段计算适应度值再求和,因此适应度计算的复杂度为O(R·N2)。
(7)最优解更新执行复杂度 将种群的解进行比较,取最优,复杂度为O(NI)。
(8)初始化操作 初始化解与算子得分,复杂度为O(N2)。
算法一次迭代的复杂度为:
若选择LLH-L或LLH-M算子,复杂度为:
O(HH)=O(O(NI·(O(1)+O(R·N2)))+
O(NI·O(1))+O(NI)+O(NL)+O(NL))
=O(NI·R·N2);
(19)
若选择LLH-LR算子,复杂度为:
O(HH)=O(O(NI·(O(N2)+O(R·N2)))+
O(NI·O(1))+O(NI)+O(NL)+O(NL))
=O(NI·R·N2)。
(20)
则算法的总复杂度为:
O(HH)=O(N2)+Gmax·O(O(NI·(O(N2)+
O(R·N2)))+O(NI·O(1))+O(NI)+
O(NL)+O(NL))=O(Gmax·
NI·R·N2)。
(21)
由上述分析可知,算法的整体计算复杂度约为O(Gmax·R·NI·N2),即算法上层策略包括选择函数以及接受准则的复杂度可以忽略不计。影响算法复杂度因素主要包括:算法的迭代次数Gmax、种群规模NI、时间分段R以及客户点规模N。对于一般的用于解决旅行商问题的基于种群的算法,复杂度为O(Gmax·NI·N2),如刘欣欣[21]提出的基于片段插入的类粒群算法,其复杂度为O(Gmax·N3)(其种群规模NI=2N);冷龙龙等[20]提出量子超启发式算法用于解决低碳选址—路径问题,其算法复杂度约为Gmax·NI·O(N2)。根据算法的复杂度判断,本文所提出的基于禁忌搜索的超启发式算法属于多项式级的算法,其复杂度处于计算机可承受范围之内。
3 数值实验
实验环境Intel(R)core-i5-8250U,8 GB RAM,程序独立运行10次,并计算最优解目标函数值(Min),最优解目标函数值方差(s2),最优解目标函数值平均值(Avg)、算法运行时间(CT)和最优解改进(gM)和算法运行时间改进(gC)。
3.1 算法性能测试
为测试算法的实际性能,设计了第一个对比实验。对比数据来自于文献[11]中对TDVRPSDP算例所得的测试结果。本实验中,将基于禁忌搜索的超启发式算法(Hype-Heuristics—Tabu Search, HH-TS)和简单随机作为选择策略的超启发式算法(Hyper-Heuristics—Simple Random, HH-SR)的求解结果进行比较以评估算法高层选择策略对算法性能的影响。实验设置参数CF=100,CT=1,CW=1,迭代次数Gmax=20 000。本文采用试取法选择参数,如表3所示。实验中的速度时间分段函数如表4所示。同时,将HH-TS与文献[11]的求解结果做比较以评估算法获得最优解的能力,如表5所示。表5中左侧给出文献[11]设计的集成蚁群与禁忌搜索的新型算法(ACS-TS)所得56个测试算例最优解,其中蚂蚁数量为20,TS迭代次数为60,ACS迭代次数为300,计算机配置:Window XP.Intel(R)Core(TM)Celeron M.1.67 GHz。

表3 参数选取
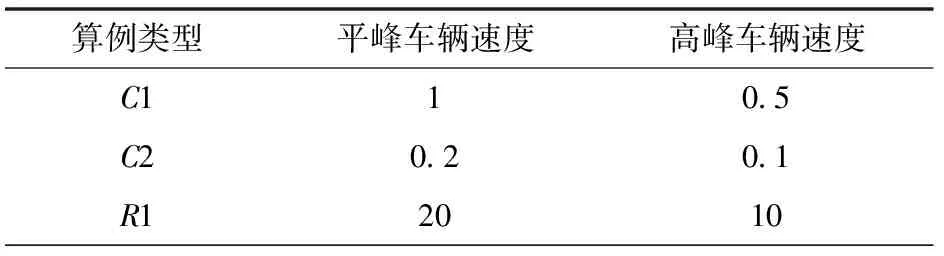
表4 配送车辆速度

表5 基于禁忌搜索的超启发式算法性能测试
表5中,gM项下展示了HH-TS与ACS-TS算法所得最优解相比较所取得的改进gM-T/A。在56个算例中,相较于ACS-TS,使用HH-TS有55个算例取得了大幅度改进。在55个取得改进的算例中,最大改进达到了58.0%,最小改进为0.8%,平均取得改进31.2%。另外,文献[11]给出了多次求解的平均值,如表5第2列。平均值只能在一定程度上反映算法的求解能力,但不能体现数据的离散程度。为保持完整性,本实验也给出了多次运行算法求解的平均值。HH-SR、HH-TS相较于ACS-TS,平均值分别取得了平均28.81%、32.02%的改进。
表5中,gM项下展示了HH-TS较HH-SR所取得的最优解改进gM-T/S,gC项下展示了HH-TS较HH-SR所取得的算法运行时间的改进gC-T/S。在56个算例中,相较于HH-SR,使用HH-TS 52个算例取得了目标函数值最大16.9%,平均4.9%的改进,此外的4个算例也取得了最差-0.5%的相对较劣的解。由此可见,超启发式算法在标准算例的求解上具有较好的优化精度。另外,HH-SR采用随机的选择函数与模拟退火接受准则作为上层策略,对3个类型底层算子进行随机的调用。HH-SR相较于HH-TS,执行无效的算子耗费了大量的时间。因此,对于同样的迭代次数,HH-TS耗时相对HH-SR大幅减少,最大92%,平均68.5%,如表5第13列所示。因此,超启发式算法较优的上层策略设计能在一定程度上,调用底层算子向函数值下降最快的方向高效地进行最优解搜索,可以保证一定的收敛速度和跳出局部最优的能力。在求解TDVRSDP时,往往超启发算法拥有更好的优势,能在短时间内求得可接受的解。
3.2 超启发式算法求解TDVRPSDP标准算例
实验增加了基于随机下降选择策略的超启发式算法(Hyper-Heuristics—Random Descent, HH-RD)实验数据,将HH-TS求解TDVRPSDP的结果与HH-SR、HH-RD对比。实验的测试实例来自于文献[22],并构造了高峰、平峰车速不同于文献[11]的速度时间分段函数,以一定的比率提高车辆速度,比率为0.5~5(如表6),得到TDVRPSDP的测试实例,如表7所示。
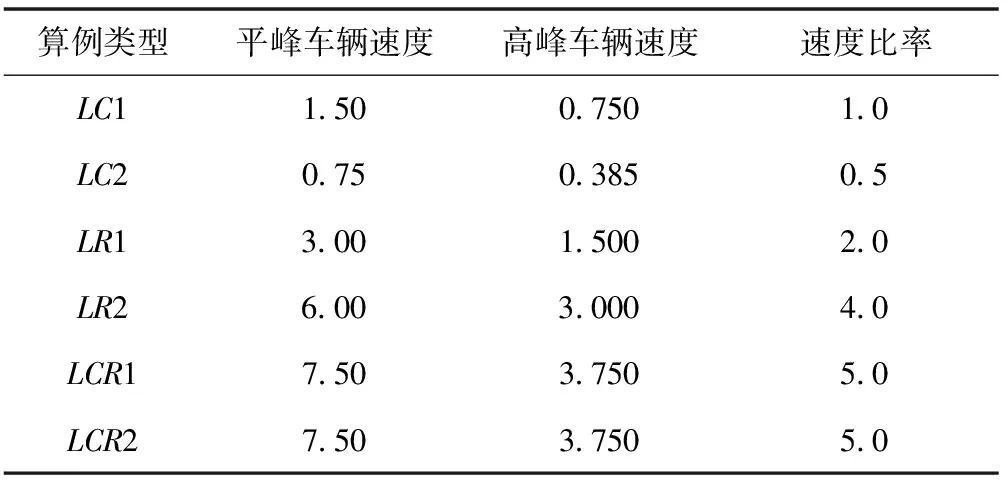
表6 配送车辆速度
文献[22]在Solomon的56个VRPTW标准测试实例的基础上,构造了6类VRPSPDPTW标准测试实例(LR1,LR2,LC1,LC2,LRC1,LRC2)并提供最优解:车辆数量(Veh)和行驶距离(Dis),如表7左侧第1和第2列所示。
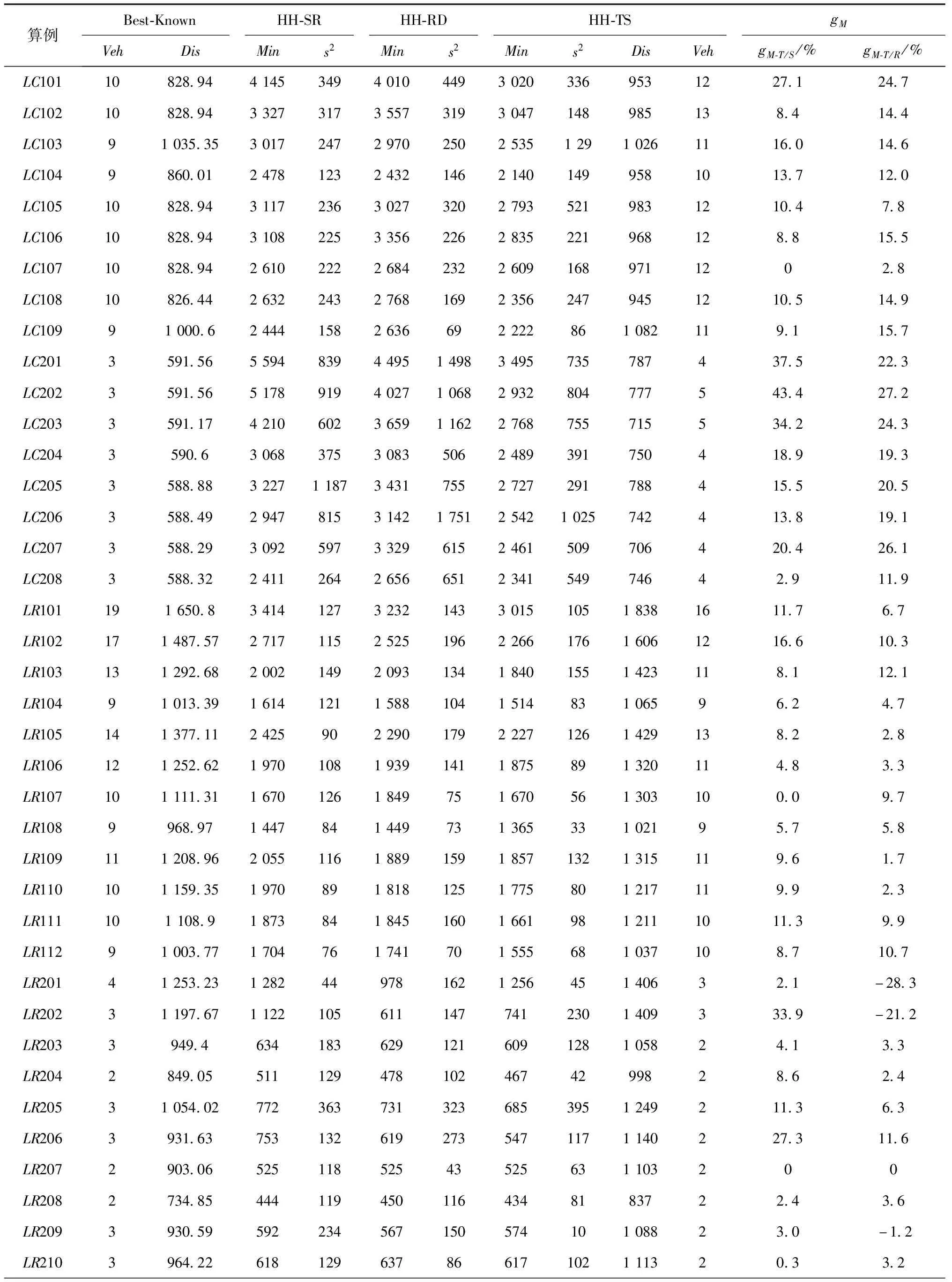
表7 TDVRPSDP实例测试
下面从模型的角度分析数据结果。表8列举了配送车辆速度变化对车辆数量及车辆总行驶距离的影响。相较于最优解,当车速增加时,配送车辆数量随车速增加而减少,但车辆的行驶距离并没有随之减少,而是微量增加。当车速取0.5和1的倍率时,较慢的车速使得配送车辆满足客户点时间窗的能力降低,车辆最大容量在一定程度上已不再是限制单车配送多个客户点的关键因素。因此,单车可访问客户点的数量下降,需要派发更多车辆才能保证每个客户点的配送时效。例如,在0.5倍速时,对于LC1算例,车辆数量增加41.67%,车辆行驶距离增加21.37%,如表8第2行。因此,车辆的出发成本与旅行成本较高,总成本较高。反之,车速取2、4和5倍速率时,配送车辆满足客户点时效要求的能力升高,单车可访问客户点数量上升,但是受限于车辆的最大容量,单车可访问客户点数量少量增加,使用车辆数量不会大量减少。同时,随着车速提高,单位时间车辆使用成本不变(CT=1),单位时间车辆可行驶距离变为原来的0.5、1、2、4、5倍。车辆的行驶时间大幅减少,因此车辆的旅行成本大幅降低,总成本降低。总结如下:①当车速提高时,使用车辆数量逐渐减少,受限于车辆最大容量,车辆数量减少数量终将到达一个固定的极限;②随车速提高,车辆行驶距离少量增加,车辆的旅行成本大幅降低,物流配送成本大幅降低,如表7第8列。因此,由实验结果可知:当车速提高时,增大车辆容量将有效减少车辆的使用数量,减少所有车辆总的行驶时间,有效地降低成本。
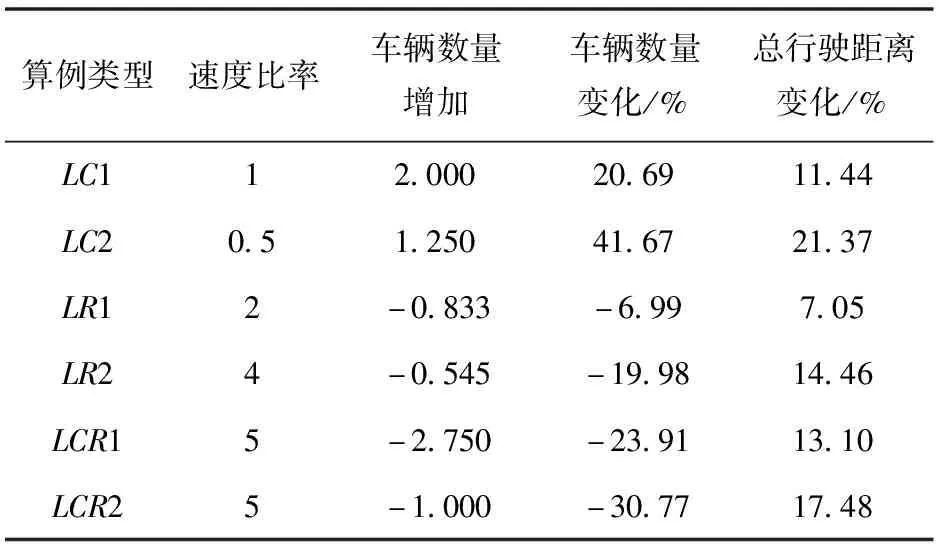
表8 配送车辆速度对车辆数量及总行驶距离的影响
从算法角度分析,HH-TS取得最优的计算结果。表7Min项下分别展示了HH-TS与HH-SR算法所的最优解相比较所取得的改进gM-T/S,HH-TS与HH-RD比较所取得的改进gM-T/R。在56个算例中,HH-TS相对于HH-SR,全部算例均取得了更优的解,最大改进43.4%,平均改进12.9%。同时,相较于HH-RD,53个算例取得了更优的解,最大改进27.2%,平均改进9.1%。HH-SR、HH-RD和HH-TS在全部算例的计算结果得到的平均方差分别为230、282和205。可以从方差的角度分析3种策略算法对求解TDVRPSDP最优解的离散程度。SR策略因其随机地选择LLH对最优解进行搜索,在有限的迭代之后通常得不到最优解,而RD策略具有一定的避免选择无效LLH的能力,但无法选择最有效的那些算子,所以仅具有微弱的跳出局部最优的能力,求解结果波动较大。TS策略根据评分选择禁忌表外的LLH,且以轮盘赌方式分配L、M和LR被选择的概率。因此,HH-TS每次求得最优解的波动也最小,性能也最好。
由此可见,上层策略的设计对解空间的搜索效率起着至关重要的作用,较好的上层策略不但能取得更好的解,而且所得结果波动较小,可以获得更好地收敛曲线并保证跳出局部最优的能力。因此,计算结果说明了禁忌搜索为选择策略的超启发式算法在求解TDVRPSDP上的有效性。
4 结束语
本文研究了时间依赖型同时取送货车辆路径问题,将配送中心的开放时间等分为3段,每段对应不同的车辆旅行速度,以车辆的租赁成本、车辆旅行成本以及车辆等待的惩罚成本之和为目标建模。设计了基于禁忌搜索的超启发式算法,高层选择策略采用禁忌搜索机制,依据算子的性能选择最有希望改进当代解的算子进行搜索,算子性能的评分由其历史表现决定,并逐代更新;高层接收准则采用模拟退火机制,保证了算法前期的快速收敛,算法中后期以一定的概率接受非改进解,使算法具备了跳出局部最优的能力。最后,通过标准算例及实验对比表明,算法在求解该问题上能较快速地取得可接受的解。对于时间依赖型车辆路径问题,车速与配送成本的关系较为复杂,后续将围绕更加复杂的车辆旅行速度以及可变车速下客户满意度、配送成本、能源消耗与行车路径之间的关系对问题模型展开研究。此外,尽管超启发式算法在求解TDVRPSDP上表现出良好的性能,但仍然具有一定的改进空间,未来考虑将超启发式算法与其他策略结合,开发出更加高效的上层策略。

